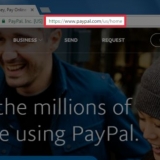
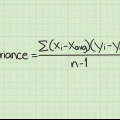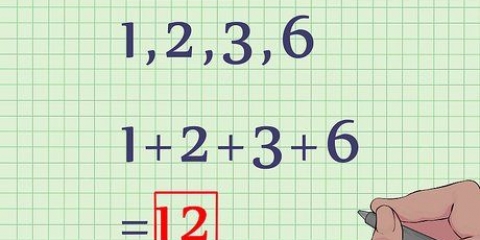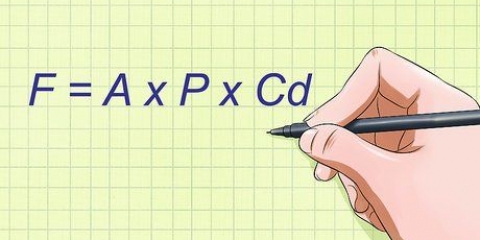17 - 14 = 3 15 - 14 = 1 23 - 14 = 9 7 - 14 = -7 9 - 14 = -5 13 - 14 = -1 3 = 9 1 = 1 9 = 81 (-7)= 49 (-5) = 25 (-1)= 1 s = 166/(6-1)
Beräkna varians
Genom att beräkna variansen kan du mäta spridningen av en uppsättning värden - i vilken grad ett antal värden skiljer sig från varandra. Varians är en av komponenterna i sannolikhetsfördelningen och anger i vilken utsträckning värden avviker från medelvärdet. Varians används ofta tillsammans med standardavvikelsen (kvadratroten av variansen). Om du vill veta hur man beräknar variansen för en uppsättning värden, följ stegen nedan.
Steg

1. Skriv formeln för att beräkna variansen. Uppskattningen för att beräkna en slumpmässig uppskattning av populationsvariansen från ett fast urval av n observationer är följande definition:(s) = Σ [(xi - x̅)]/n - 1. Formeln för att beräkna variansen i en hel population är densamma som den föregående, förutom att nämnaren inte är lika med n – 1, utan med n. Så länge du har att göra med en ändlig uppsättning observationer är det bättre att använda den första formeln. Här är en förklaring av formelns variabler:
- s = Varians
- Σ = Summation, summan av alla termer i ekvationen efter summeringstecknet.
- Xi = Exempelvärdena.
- x̅ = Medelvärdet av värdena i serien.
- n = Provstorleken. Antalet värden i serien.
2. Beräkna summan av värdena i serien. Skapa först en tabell med en kolumn för värdena, värdet minus medelvärdet (xi - x̅) och sedan kvadraten på dessa termer [(xi - X))]. När du är klar med tabellen och fyllt i den första kolumnen lägger du ihop alla värden i serien. Anta att du har att göra med följande nummersekvens: 17, 15, 23, 7, 9, 13. Sammanlagt är detta: 17 + 15 + 23 + 7 + 9 + 13 = 84.
3. Beräkna medelvärdet. Dela summan av talen i serien med antalet element i serien för att beräkna medelvärdet. Så i det här fallet summan 84 dividerat med antalet siffror, 6. 84/6 = 14. skriva "14" längst ner i kolumnen som ett genomsnitt.
4. Subtrahera medelvärdet av varje värde i serien. Subtrahera 14 från varje värde i serien och fyll i den tredje kolumnen (provmedelvärdet). Du kan kontrollera ditt arbete genom att kontrollera om summan av alla resultat är noll. Så här beräknar du avvikelsen från medelvärdet för varje värde i serien:
5. Kvadra varje resultat. Efter att ha beräknat avvikelsen från medelvärdet, kvadrera det och skriva svaret i den fjärde kolumnen. Så alla svar är positiva. Så här gick det till:
6. Beräkna summan av kvadrater. Lägg ihop resultaten. 9 + 1 + 81 + 49 + 25 + 1 = 166
7. Byt ut värdena i ekvationen. Fyll i värdena i ekvationen. Kom ihåg det "n" representerar antalet element i sekvensen.
8. Lösa. Dela nu 166 med 5. Resultatet är 33,2. Om du också vill veta standardavvikelsen, hitta kvadratroten ur 33,2. √33,2 = 5,76. Nu kan du börja tolka denna data i förhållande till helheten. Vanligtvis jämförs variansen för två serier. Det lägsta värdet betyder att i den serien är variansen mindre stor.
Tips
- Eftersom det kan vara svårt att tolka varians, beräknas detta värde vanligtvis bara som början på standardavvikelseberäkningen.
Оцените, пожалуйста статью