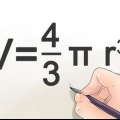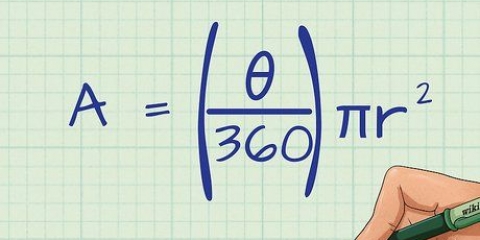Anta att du får veta att det finns en sfär med en radie på 10 cm. Hitta volymen enligt följande: 





Som ett exempel på denna beräkning, bestäm volymen av en sfär med en diameter på 10 cm. 















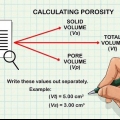
Häll tillräckligt med vatten i koppen för att täcka glödlampan. Notera volymen. Häll glödlampan i vattnet. Observera att vattennivån stiger. Notera den nya volymen. Subtrahera den första volymen från den andra. Resultatet är sfärens volym. Anta att din vattennivå stiger från 100 ml till 625 ml när du sänker ner glödlampan. Så volymen är 525 ml. Observera att 1 ml=1 cm. 

Alla exempel i föregående avsnitt resulterade i volymer mätt i kubikcentimeter. Den angivna densitetstabellen ger dock densiteter baserat på kubikmeter. Eftersom det finns 100 centimeter i en meter, finns det 10 kubikcentimeter i en kubikmeter. Dividera de givna tätheterna med 10 för att få densiteten i enheter av kg/cm (enkelt att göra genom att flytta decimalkomma sex mellanslag åt vänster). För de fyra tidigare listade materialen är de konverterade densiteterna som följer: Aluminium = 2700 kg/m = 0,0027 kg/cm Smör = 870 kg/m3 = 0,00087 kg/cm Bly = 11.350 kg/m = 0,01135 kg/cm Pressat trä = 190 kg/m = 0,00019 kg/cm 
Med hjälp av de fyra tidigare nämnda materialen, aluminium, smör, bly och pressat trä, bestämmer du massan på en sfär med en volym på 500 cm. 






Du läste också att sfären är gjord av mässing. Du måste leta upp tätheten av mässing i din Binas eller från en annan källa. På hemsidan, EngineeringToolbox.com kan du slå upp att densiteten för mässing är 8480 kg/m. Eftersom sfärens diameter anges i meter, beräknas dess volym i kubikmeter, så du behöver inte konvertera densiteten. 









Beräkna massan av en sfär
Enkelt uttryckt är en sfär en solid rund boll. För att beräkna massan av en sfär måste du veta storleken (volymen) av sfären och dess densitet. Du kan beräkna volymen med hjälp av sfärens radie, omkrets eller diameter. Du kan också sänka sfären i vatten för att hitta volymen genom vattenförskjutning. Om du känner till volymen kan du multiplicera den med densiteten för att hitta massan.
Steg
Del 1 av 3: Bestämma volymen av en sfär

1. Använd formeln för volymen av en sfär. En sfär är en cirkulär solid i tre dimensioner. Den primära formeln för volymen av en sfär är:

2. Hitta volymen på en sfär om du vet dess radie. En sfärs radie är måttet från sfärens centrum till den yttre kanten. Om du får ett problem att beräkna volymen, är radien förmodligen given. Annars kan radien vara svår att mäta eftersom du inte kan exakt bestämma mitten av ett fast föremål.





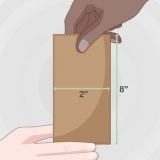
3. Bestäm volymen om diametern är angiven. En annan möjlighet är att för en viss situation anges en sfärs diameter. Diametern är lika med två gånger radien. I själva verket är diametern avståndet från en kant av sfären genom mitten till den andra kanten. För att beräkna volym från diameter (d), ändra formeln enligt följande:







4. Revidera formeln om du känner till omkretsen. Omkretsen av en sfär är förmodligen den lättaste att mäta direkt. Du kan använda ett måttband, linda det försiktigt runt den bredaste delen av glödlampan och ta måttet. Kanske anges omkretsen i ett uttalande. För att hitta volymen som börjar med omkretsen (C), ändra formeln enligt följande:





5. Beräkna volymen om du känner till omkretsen. Anta att du får en sfär och du mäter omkretsen på 32 cm. Hitta volymen enligt följande:





6. Mät volymen genom vattenförskjutning. En sista praktisk metod för att mäta volymen är att sänka ner glödlampan i vatten. Du måste ha en bägare som är tillräckligt stor för att sänka ner glödlampan med exakta volymmarkeringar.
Del 2 av 3: Beräkna massa från volym

1. Bestäm densiteten. För att beräkna massan från volymen måste du känna till föremålets densitet. Olika material har olika densitet. Tänk till exempel på en klot av frigolit och jämför dess vikt med en sfär av samma storlek av järn. Järn har en mycket större densitet och kommer därför att ha en större massa.
- Du kan slå upp tätheter av många fasta material online, i läroböcker eller i en Binas.
- Till exempel, här är de registrerade densiteterna för vissa fasta material:
- Aluminium = 2700 kg/m
- Smör = 870 kg/m
- Bly = 11.350 kg/m
- Pressat trä = 190 kg/m

2. Konvertera enheterna efter behov. Enheterna du använder när du beräknar volymen måste matcha volymenheterna i den uppmätta densiteten. Om inte, måste du konvertera dem.

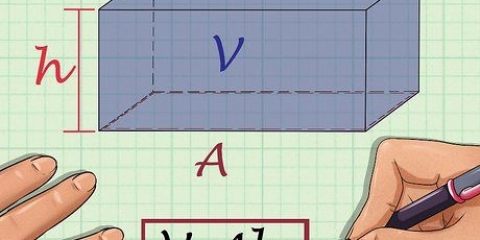
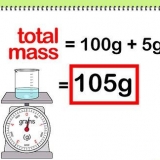
3. Multiplicera volymen med densiteten för att hitta massan. Formeln för densiteten är  , som du kanske minns. Om du ordnar om detta för att hitta massan blir ekvationen
, som du kanske minns. Om du ordnar om detta för att hitta massan blir ekvationen  .
.
 , som du kanske minns. Om du ordnar om detta för att hitta massan blir ekvationen
, som du kanske minns. Om du ordnar om detta för att hitta massan blir ekvationen  .
.



Del 3 av 3: Lösa ett exempelproblem

1. Läs uppgiften noggrant. När du svarar på problem med massberäkningar, läs hela påståendet noggrant. När du läser kan det hjälpa att markera inlägget. Läs hela problemet noggrant för att se vad du kommer att bli ombedd att lösa. Tänk till exempel på följande problem:
- En stor klot av massiv mässing har en diameter på 1,2 m. Bestäm massan av sfären.

2. Organisera kända och okända data. Om du läser uttalandet noggrant kan du bestämma att diametern är given, så använd den modifierade formeln:


3. Beräkna volymen. För att beräkna volym, skriv in lämplig formel, fyll i uppgifterna du känner till och utför beräkningarna enligt följande:






4. Använd densitet för att beräkna massa. Tror att  . Ange de värden du känner till i formeln för att hitta massan:
. Ange de värden du känner till i formeln för att hitta massan:
 . Ange de värden du känner till i formeln för att hitta massan:
. Ange de värden du känner till i formeln för att hitta massan:


Tips
- Denna förklaring antar att sfärens täthet är densamma överallt. Detta antas i de flesta matematiska och fysikaliska problem. Det är dock möjligt att kärnan i en sfär är gjord av ett annat material än ytan.
"Beräkna massan av en sfär"
Оцените, пожалуйста статью