bol: där r är sfärens radie.
där r är sfärens radie. Kon: där r är radien på den cirkulära basen och h är höjden på konen.
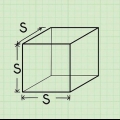
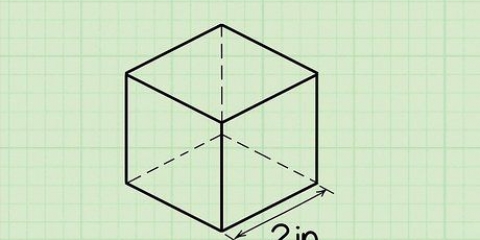
där r är radien på den cirkulära basen och h är höjden på konen. Kub:  där s är längden på en sida.
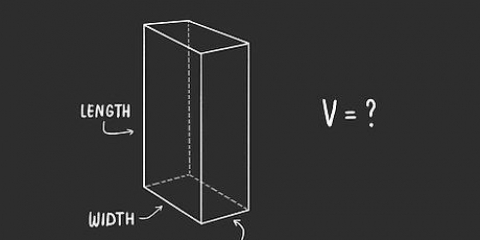
där s är längden på en sida. Rektangulärt prisma:  där l är längden på en sida av en rektangulär yta, w är bredden på en rektangulär yta och h är höjden på prismat.
där l är längden på en sida av en rektangulär yta, w är bredden på en rektangulär yta och h är höjden på prismat. Cylinder:  där r är radien på den cirkulära basen och h är höjden på konen.
där r är radien på den cirkulära basen och h är höjden på konen. Pyramid:  där B är arean av pyramidens bas och h är höjden på pyramiden.
där B är arean av pyramidens bas och h är höjden på pyramiden. 
En cirkels radie är halva dess diameter. Mät diametern med en linjal genom mitten av cirkeln och läs av avläsningen. Beräkna radien genom att dividera diametern med två. Att bestämma radien för en sfär kräver lite mer ansträngning, men kan göras på flera sätt, som visas i Denna artikel. Objektens längd, bredd och höjd kan mätas med en linjal, mäta från ena änden av ett objekt till den andra. 
Glöm inte att ge ditt svar i kubikenheter. Oavsett om du använder mått eller SI är volymenheten alltid kubik. Lägg alltid till enheter i slutet av din beräkning. 

När du mäter den initiala vattenvolymen, titta på vätskenivån i ögonhöjd och notera avläsningen på undersidan av menisken. Menisken är kurvan som vatten gör när det kommer i kontakt med en yta. 
Om du spillde vatten när du placerade föremålet i koppen, försök igen med en större mätkopp, eller använd mindre vatten. 
Anta till exempel att du började med 35 ml vatten och slutade med 65 ml vatten; volymen på ditt föremål är då 65 – 35 = 30 ml eller 30 cm 


Beräkna till exempel densiteten  av ett ämne med en volym av 8 cm och en massa av 24 g.
av ett ämne med en volym av 8 cm och en massa av 24 g. 
Beräkna volym och densitet
Volym är mängden utrymme ett objekt upptar medan densitet är objektets massa per volymenhet. Du måste först veta volymen av ett föremål innan du kan beräkna dess densitet. Du kan beräkna volymen för vanliga objekt med en enkel formel, bestäms av formen på objektet. Vanliga enheter för volym är kubikcentimeter (cm) och kubikmeter (m). När du har räknat ut volymen så bestäms densiteten med en enkel beräkning. Vanligt använda enheter för densitet är gram per kubikcentimeter (g/cm) eller gram per milliliter (g/mL).
Steg
Del 1 av 3: Beräkna volymen av ett vanligt föremål

1. Bestäm formen på föremålet. Genom att känna till formen på ett föremål kan du bestämma den korrekta formeln och göra de nödvändiga beräkningarna för volymen.
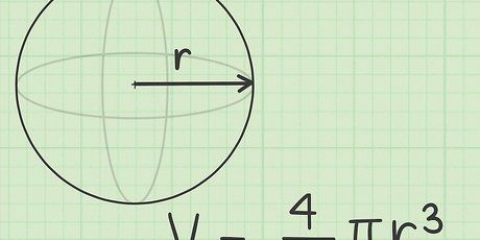
- A sfär är ett perfekt runt tredimensionellt objekt, där varje punkt på dess yta är lika långt från mitten. Med andra ord är en sfär ett sfäriskt föremål.
- A kon är ett tredimensionellt föremål med en cirkulär bas och en punkt. Ett annat sätt att tänka på detta är att en kon är en speciell sorts pyramid med en cirkulär bas.
- A kub är en tredimensionell form med sex identiska fyrkantiga ytor.
- A parallellepiped, även kallat ett rektangulärt prisma, ser ut som en kub eftersom det är en tredimensionell form med sex sidor, men i det här fallet är sidorna rektangulära istället för kvadratiska.
- A cylinder är en tredimensionell form med två identiska platta cirklar och en enda böjd plan yta som förbinder båda cirklarna.
- A pyramid är en tredimensionell form med en polygon som bas och lutande sidor som möts vid en punkt (pyramidens spets).En vanlig pyramid är en pyramid med en vanlig polygon som bas för pyramiden, vilket betyder att alla sidor av polygonen är lika långa och alla vinklar är lika stora.
- Om ditt föremål har en oregelbunden form kan du använda förskjutningsmetoden för att bestämma dess volym.

2. Välj rätt ekvation för att beräkna volym. Varje form har sin egen formel för att beräkna hur mycket tredimensionellt utrymme den tar upp. Nedan hittar du formlerna för de tidigare nämnda objekten. Läs mer om det beräkna volymen för mer detaljerade exempel och bilder på dessa formler.
 där r är sfärens radie.
där r är sfärens radie. där r är radien på den cirkulära basen och h är höjden på konen.
där r är radien på den cirkulära basen och h är höjden på konen. där s är längden på en sida.
där s är längden på en sida. där l är längden på en sida av en rektangulär yta, w är bredden på en rektangulär yta och h är höjden på prismat.
där l är längden på en sida av en rektangulär yta, w är bredden på en rektangulär yta och h är höjden på prismat. där r är radien på den cirkulära basen och h är höjden på konen.
där r är radien på den cirkulära basen och h är höjden på konen. där B är arean av pyramidens bas och h är höjden på pyramiden.
där B är arean av pyramidens bas och h är höjden på pyramiden.
3. Gör nödvändiga mätningar. Måtten du behöver bestäms av formen på föremålet. För de flesta objekt behöver du höjden, men radien är tillräcklig om formen är cirkulär, eller längden och bredden på objekt med rektangulära ytor.

4. Beräkna volymen. Nu när du har bestämt formen, vet vilken formel du ska använda och har tagit de nödvändiga måtten, kan du beräkna volymen. Ange dina avläsningar och utför nödvändiga beräkningar. Slutprodukten är volymen på ditt föremål.
Del 2 av 3: Beräkna volymen av ett oregelbundet föremål

1. Beräkna volymen på föremålet med hjälp av förskjutning. Det kan vara svårt att bestämma dimensionerna på oregelbundet formade föremål, vilket i efterhand leder till felaktiga mätningar och volymberäkningar. Genom att mäta hur mycket vatten som förskjuts av ett föremål kan du beräkna dess volym utan komplexa formler.
- Denna metod kan också användas för att beräkna volymen av en vanlig form.

2. Fyll en graderad cylinder med vatten. En graderad cylinder är ett laboratorieinstrument med markeringar på utsidan och låter dig mäta volymen av en viss mängd vätska. Se till att den graderade cylindern är tillräckligt stor för att hålla föremålet. Fyll den med tillräckligt med vatten så att föremålet är helt nedsänkt, men vattnet rinner inte ut över kanten. Notera den initiala nivån på vattnet.

3. Placera föremålet lugnt i koppen. Var försiktig så att du inte tappar föremålet i vattnet, annars kan vatten rinna över kanten och avläsningen blir felaktig. Se till att föremålet är helt nedsänkt i vatten. Notera den nya vattennivån i koppen, återigen i ögonhöjd, var noga med menisken.

4. Subtrahera den nya vattennivån från den ursprungliga nivån. Mängden vatten som förskjuts av föremålet är lika med föremålets volym mätt i kubikcentimeter. Vätskor mäts vanligtvis i milliliter, och en milliliter är lika med en kubikcentimeter.
Del 3 av 3: Beräkna densitet

1. Bestäm föremålets massa. Mängden materia i ett föremål är massan av det föremålet. Detta kan mätas direkt genom att placera föremålet på en skala med enheten i gram.
- Ha en exakt våg till hands och placera föremålet på den. Anteckna dess massa i din anteckningsbok.
- Du kan också mäta massa med en våg. Med föremålet på ena sidan, placera vikter med känd massa på den andra sidan av vågen tills de är i jämvikt med föremålet. Massan av ditt föremål är lika med vikternas totala massa.
- Det är viktigt att se till att ditt föremål är torrt innan du väger det. På så sätt är du säker på att mätresultatet inte blir mindre exakt på grund av det absorberade vattnet.

2. Beräkna volymen på ditt objekt. Om ditt föremål har en regelbunden form, beräkna volymen med någon av metoderna som tidigare angetts. Om formen är oregelbunden, beräkna volymen med hjälp av förskjutningsmetoden som förklaras ovan.

3. Beräkna densiteten. Densitet definieras som massan dividerad med volymen. Slutligen, för att bestämma densiteten, dividera den viktade massan med den uppmätta volymen. Resultatet är metallens densitet uttryckt i g/cm.
 av ett ämne med en volym av 8 cm och en massa av 24 g.
av ett ämne med en volym av 8 cm och en massa av 24 g.
Tips
- Du kan testa dina volymberäkningar genom att jämföra resultatet av förskjutningsmetoden och beräkningarna.
- Objekt är ofta en sammansättning av flera geometriska objekt, så du kan dela upp dem i mindre grundläggande grupper för att bestämma volymen för varje, och sedan lägga ihop dem alla för att bestämma objektets volym.
Varningar
- Se till att du har alla mätningar i metriska eller SI-enheter innan du fortsätter med dina beräkningar.
"Beräkna volym och densitet"
Оцените, пожалуйста статью