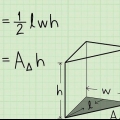
I exemplet är sidorna av pyramidens bas alla 5 cm, och du beräknar basens yta enligt följande: 
Kom ihåg att tvådimensionella områden uttrycks i kvadrater – kvadratcentimeter, meter, kilometer, etc. 
I exemplet antar vi att pyramiden har en höjd av 9 cm. I det här fallet, multiplicera arean av basen med detta värde, enligt följande: 
Kom ihåg att volymer uttrycks i kubikenheter. I det här fallet, eftersom alla linjära mått är centimeter, anges volymen i kubikcentimeter. 
I exemplet dividerar du 225 cm med 3 och svaret är 75 cm för volymen. 


Denna ersättning ser ut så här: 


 .....(ursprunglig ekvation)
.....(ursprunglig ekvation) .....(ruta på båda sidor)
.....(ruta på båda sidor) .....(skriv in värden)
.....(skriv in värden) .....(förenkla bråk)
.....(förenkla bråk) .....(förenkla kvadrat)
.....(förenkla kvadrat) .....(subtrahera)
.....(subtrahera) .....(förenkla root)
.....(förenkla root)
Av beräkningarna drar vi slutsatsen att höjden på pyramiden är 12 cm. Använd detta tillsammans med 10 cm-sidan av basen för att beräkna pyramidens volym: 









 ..........(justerad ekvation)
..........(justerad ekvation) ..........(ersätt h på båda sidor)
..........(ersätt h på båda sidor) ..........(subtrahera kvadratroten från båda sidorna)
..........(subtrahera kvadratroten från båda sidorna) ..........(fyll i siffrorna)
..........(fyll i siffrorna) ..........(förenkla rutorna)
..........(förenkla rutorna) ..........(subtrahera värden)
..........(subtrahera värden) ..........(förenkla kvadratroten)
..........(förenkla kvadratroten)Dubbla detta värde för att hitta diagonalen för pyramidens kvadratiska bas. Således är diagonalen för pyramidens bas 9,8 * 2 = 19,6 cm. 
I detta pyramidexempel är basens diagonal 19,6 cm. Därför är sidan lika med: 





Beräkna volymen av en kvadratisk pyramid
En fyrkantig pyramid är en tredimensionell figur med en kvadratisk bas och triangulära lutningar som möts i en punkt ovanför basen. I händelse av att 


Steg
Metod 1 av 3: Bestäm volymen med basens yta och höjden

1. Mät längden på sidan av basen. Eftersom fyrkantiga pyramider per definition har en kvadratisk bas, bör alla sidor av basen ha lika långa. Så med en fyrkantig pyramid behöver du bara veta längden på en av sidorna.
- Anta att du har en pyramid med en kvadratisk bas vars sidor har en längd av
. Du kommer att använda detta värde för att beräkna arean av basen.
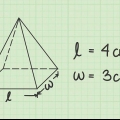
- Om basens sidor inte är lika långa har du en rektangulär pyramid istället för en fyrkantig pyramid. Formeln för volymen av en rektangulär pyramid är mycket lik formeln för kvadratiska pyramider. I händelse av att
är längden på basen av den rektangulära pyramiden och
bredden, sedan volymen av pyramiden
.

2. Beräkna arean av basen. För att bestämma volymen behöver du först arean av basen. Det gör du genom att multiplicera basens längd och bredd. Eftersom basen av en fyrkantig pyramid är en kvadrat, har alla sidor samma längd, och basens yta är lika med kvadraten på längden på en av dess sidor (alltså multiplicerad med sig själv).


3. Multiplicera arean av basen med höjden på pyramiden. Sedan multiplicerar du basytan med höjden på pyramiden. Som en påminnelse, höjden är avståndet är längden av linjesegmentet från toppen av pyramiden till basen, i rät vinkel.


4. Dela det här svaret med 3. Slutligen bestämmer du volymen på pyramiden genom att dividera värdet du just hittade (genom att multiplicera arean av basen med höjden) med 3. Detta beräknar volymen av den kvadratiska pyramiden.
Metod 2 av 3: Bestäm volymen med apotem

1. Mät pyramidens apotem. Ibland anges inte pyramidens vinkelräta höjd (eller så måste du mäta den), utan apotem. Med apotem kan du använda Pythagoras sats använd för att beräkna vinkelrät höjd.
- En pyramids apotem är avståndet från spetsen till mitten av en av sidorna av dess bas. Mät till mitten av en av sidorna och inte till ett av hörnen på basen. För det här exemplet antar vi att apotem är 13 cm och längden på ena sidan av basen är 10 cm.
- Kom ihåg att Pythagoras sats kan uttryckas som ekvationen
, varigenom
och
de vinkelräta benen är av rät triangel och
hypotenusan.

2. Föreställ dig en rätvinklig triangel. För att använda Pythagoras sats behöver du en rätvinklig triangel. Föreställ dig en triangel som delar pyramiden på mitten och vinkelrätt mot pyramidens bas. Pyramidens apotem, kallad  , är hypotenusan för denna räta triangel. Basen av denna rätvinkliga triangel är halva längden av
, är hypotenusan för denna räta triangel. Basen av denna rätvinkliga triangel är halva längden av  , sidan av pyramidens kvadratiska bas.
, sidan av pyramidens kvadratiska bas.
 , är hypotenusan för denna räta triangel. Basen av denna rätvinkliga triangel är halva längden av
, är hypotenusan för denna räta triangel. Basen av denna rätvinkliga triangel är halva längden av  , sidan av pyramidens kvadratiska bas.
, sidan av pyramidens kvadratiska bas.
3. Tilldela variabler till värdena. Pythagoras sats använder variablerna a, b och c, men det är bra att ersätta dem med variabler som är meningsfulla för ditt problem. apotem  tar platsen för
tar platsen för  i Pythagoras sats. Benet i den högra triangeln (
i Pythagoras sats. Benet i den högra triangeln ( ), tar platsen för
), tar platsen för  Du går höjden
Du går höjden  bestämma pyramiden, som upptar platsen för
bestämma pyramiden, som upptar platsen för  i Pythagoras sats.
i Pythagoras sats.
 tar platsen för
tar platsen för  i Pythagoras sats. Benet i den högra triangeln (
i Pythagoras sats. Benet i den högra triangeln ( ), tar platsen för
), tar platsen för  Du går höjden
Du går höjden  bestämma pyramiden, som upptar platsen för
bestämma pyramiden, som upptar platsen för  i Pythagoras sats.
i Pythagoras sats.


4. Använd Pythagoras sats för att beräkna den vinkelräta höjden. Använd de uppmätta värdena  och
och  . Lös sedan ekvationen:
. Lös sedan ekvationen:
 och
och  . Lös sedan ekvationen:
. Lös sedan ekvationen: .....(ursprunglig ekvation)
.....(ursprunglig ekvation) .....(ruta på båda sidor)
.....(ruta på båda sidor) .....(skriv in värden)
.....(skriv in värden) .....(förenkla bråk)
.....(förenkla bråk) .....(förenkla kvadrat)
.....(förenkla kvadrat) .....(subtrahera)
.....(subtrahera) .....(förenkla root)
.....(förenkla root)
5. Använd höjd och bas för att beräkna volym. Efter att ha tillämpat dessa beräkningar på Pythagoras sats har du nu den information du behöver för att beräkna volymen på pyramiden. Använd formeln  och lös dessa, se till att ge svaret i kvadratiska enheter.
och lös dessa, se till att ge svaret i kvadratiska enheter.
 och lös dessa, se till att ge svaret i kvadratiska enheter.
och lös dessa, se till att ge svaret i kvadratiska enheter.



Metod 3 av 3: Bestämma volymen med höjden på benen

1. Mät höjden på pyramidens ben. Höjden på benen är längden på pyramidens kanter, mätt från toppen till ett av hörnen på basen. Som ovan, använd Pythagoras sats för att beräkna pyramidens vinkelräta höjd.
- I detta exempel antar vi att höjden på benen är 11 cm och att den vinkelräta höjden är 5 cm.

2. Föreställ dig en rätvinklig triangel. Återigen behöver du en rätvinklig triangel för att kunna använda Pythagoras sats. I det här fallet är dock det okända värdet pyramidens bas. Känd är den vertikala höjden och höjden på benen. Föreställ dig nu att du skär pyramiden diagonalt från ett hörn till det andra hörnet och öppnar sedan figuren, det resulterande planet kommer att se ut som en triangel. Höjden på den triangeln är pyramidens vinkelräta höjd. Detta delar upp den exponerade triangeln i två symmetriska räta trianglar. Hypotenusan för var och en av de räta trianglarna är höjden på pyramidens ben. Basen för var och en av de räta trianglarna är halva diagonalen av pyramidens bas.

3. Tilldela variabler. Använd den imaginära räta triangeln och tilldela värden till Pythagoras sats. Du vet den vertikala höjden,  som är ena sidan av Pythagoras sats,
som är ena sidan av Pythagoras sats,  . Höjden på pyramidens ben,
. Höjden på pyramidens ben,  bildar hypotenusan för denna imaginära räta triangel och tar därför platsen för
bildar hypotenusan för denna imaginära räta triangel och tar därför platsen för  . Den okända diagonalen för pyramidens bas är den återstående sidan av den räta triangeln,
. Den okända diagonalen för pyramidens bas är den återstående sidan av den räta triangeln,  Efter att ha gjort dessa substitutioner ser ekvationen ut så här:
Efter att ha gjort dessa substitutioner ser ekvationen ut så här:
 som är ena sidan av Pythagoras sats,
som är ena sidan av Pythagoras sats,  . Höjden på pyramidens ben,
. Höjden på pyramidens ben,  bildar hypotenusan för denna imaginära räta triangel och tar därför platsen för
bildar hypotenusan för denna imaginära räta triangel och tar därför platsen för  . Den okända diagonalen för pyramidens bas är den återstående sidan av den räta triangeln,
. Den okända diagonalen för pyramidens bas är den återstående sidan av den räta triangeln,  Efter att ha gjort dessa substitutioner ser ekvationen ut så här:
Efter att ha gjort dessa substitutioner ser ekvationen ut så här:


4. Beräkna diagonalen för den kvadratiska basen. Du måste ändra ordning på ekvationen för att få variabeln  isolera och beräkna sedan dess värde.
isolera och beräkna sedan dess värde.
 isolera och beräkna sedan dess värde.
isolera och beräkna sedan dess värde. ..........(justerad ekvation)
..........(justerad ekvation) ..........(ersätt h på båda sidor)
..........(ersätt h på båda sidor) ..........(subtrahera kvadratroten från båda sidorna)
..........(subtrahera kvadratroten från båda sidorna) ..........(fyll i siffrorna)
..........(fyll i siffrorna) ..........(förenkla rutorna)
..........(förenkla rutorna) ..........(subtrahera värden)
..........(subtrahera värden) ..........(förenkla kvadratroten)
..........(förenkla kvadratroten)
5. Hitta sidan av basen av diagonalen. Basen på pyramiden är en kvadrat. Diagonalen för varje kvadrat är lika med längden på en av dess sidor, gånger kvadratroten 2. Och så kan du hitta sidan på en kvadrat genom att dividera diagonalen med kvadratroten 2.


6. Beräkna volymen med hjälp av sidan och höjden. Återgå till den ursprungliga formeln för att beräkna volymen med hjälp av sida och vinkelrät höjd.




Tips
- I en kvadratisk pyramid kan den vinkelräta höjden, apotem och längden på kanten av basen alla beräknas med hjälp av Pythagoras sats.
"Beräkna volymen av en kvadratisk pyramid"
Оцените, пожалуйста статью