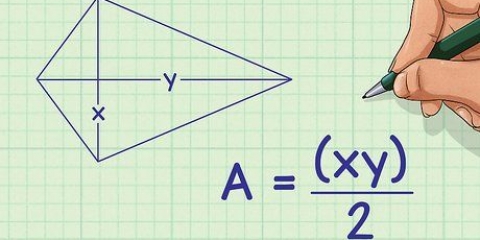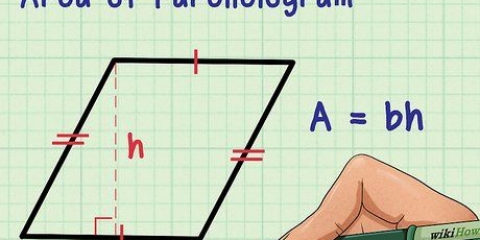Till exempel, om volymen på prismat är 64  ), din formel kommer att se ut så här:
), din formel kommer att se ut så här:


Till exempel, om basen är en rektangel 8 meter lång och 2 meter bred, skulle du beräkna arean enligt följande:



Till exempel, om du beräknade att arean på basen är 16 m, kommer din formel att se ut så här:


Till exempel i ekvationen  , du måste dividera varje sida med 16 om
, du måste dividera varje sida med 16 om  att räkna ut. Således:
att räkna ut. Således:


Så höjden på det rektangulära prismat är 4 meter. 

Till exempel, om du vet att volymen på prismat är 840 kubikmeter ( ), din formel kommer att se ut så här:
), din formel kommer att se ut så här:


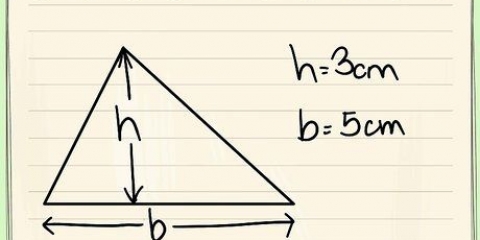
Om du vet längden på alla tre sidorna i en triangel kan du beräkna arean med Herons formel.läsa Beräkna arean av en triangel för detaljerade instruktioner. Till exempel, om basen på triangeln är 12 meter och triangelns höjd är 7 meter, hitta arean enligt följande:




Till exempel, om du vet att arean på basen är 42 m2, kommer din formel att se ut så här:


Till exempel i ekvationen  , du måste dividera varje sida med 42 för att avgöra
, du måste dividera varje sida med 42 för att avgöra  . Således:
. Således:


Så höjden på ditt triangulära prisma är 20 meter. 

Till exempel, om arean är 1460 cm, skulle din formel se ut så här:


Till exempel, om basen är en rektangel med en längd på 8 cm och en bredd på 2 cm, hitta området enligt följande:



Till exempel, om arean av basen är 16, skulle din formel se ut så här:



Kom ihåg att de motsatta sidorna av en rektangel har samma längd. Till exempel, om basen är en rektangel med en längd på 8 cm och en bredd på 2 cm, hitta omkretsen enligt följande:



Till exempel, om basens omkrets är 20, skulle din formel se ut så här:


Till exempel i ekvationen  subtrahera först 32 från varje sida, dividera sedan varje sida med 20. Således:
subtrahera först 32 från varje sida, dividera sedan varje sida med 20. Således:




Så höjden på ditt prisma är 71,4 cm. 

Till exempel, om arean är 1460 cm, skulle din formel se ut så här:


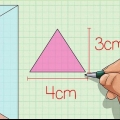
Om du vet längden på alla tre sidorna i en triangel kan du bestämma arean med Herons formel.läsa Beräkna arean av en triangel för fullständiga instruktioner. Till exempel, om basen på triangeln är 8 cm och triangelns höjd är 4 cm, skulle du beräkna arean enligt följande:




Till exempel, om arean av basen är 16, skulle din formel se ut så här:



Till exempel, om basen är en triangel med längderna 8, 4 och 9 cm, beräknar du omkretsen enligt följande:



Anta till exempel att basens omkrets är 21, din formel kommer att se ut så här:


Till exempel i ekvationen  , du måste först subtrahera 32 från varje sida och sedan dividera varje sida med 21. Således:
, du måste först subtrahera 32 från varje sida och sedan dividera varje sida med 21. Således:




Så höjden på ditt prisma är 68 cm.
Beräkna höjden på ett prisma
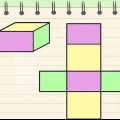
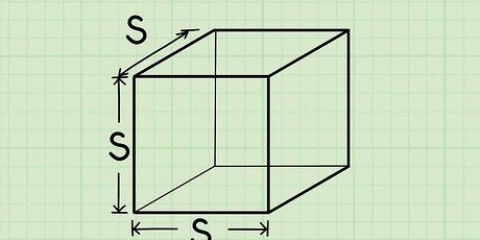
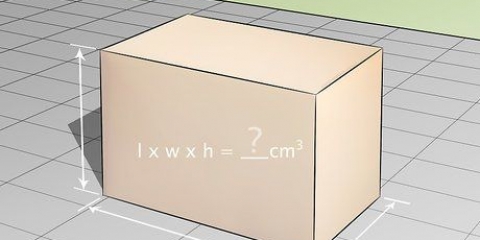
Ett prisma är en tredimensionell figur med två parallella baser, som är kongruenta.Formen på basen avgör vilken typ av prisma det är, till exempel ett rektangulärt eller triangulärt prisma. Eftersom det är en 3D-form är det inte ovanligt att man vill beräkna volymen av ett prisma; dock behöver du prismats höjd för det. Att hitta höjden är möjligt när du har fått tillräckligt med information: antingen basens volym, area och omkrets. Formlerna som beskrivs i metoderna nedan är lämpliga för prismor med baser av vilken form som helst, förutsatt att du känner till formeln för att hitta arean av den formen.
Steg
Metod 1 av 4: Hitta höjden på ett rektangulärt prisma med känd volym

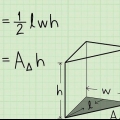
1. Använd formeln för volymen av ett prisma. Volymen av ett prisma kan hittas med hjälp av formeln  , varigenom
, varigenom  är lika med prismats volym,
är lika med prismats volym,  är lika med arean av en bas, och
är lika med arean av en bas, och  är lika med prismats höjd.
är lika med prismats höjd.
 , varigenom
, varigenom  är lika med prismats volym,
är lika med prismats volym,  är lika med arean av en bas, och
är lika med arean av en bas, och  är lika med prismats höjd.
är lika med prismats höjd. - Basen av ett prisma är en av dess kongruenta sidor. Eftersom alla motsatta sidor av ett rektangulärt prisma är kongruenta, kan vilken sida som helst användas som ett jordplan, så länge du är konsekvent med dina beräkningar.

2. Applicera volymen på formeln. Om du inte känner till volymen kan du inte använda den här metoden.
 ), din formel kommer att se ut så här:
), din formel kommer att se ut så här:

3. Hitta arean av basen. För att hitta arean måste du veta längden och bredden på basen (eller på en sida, om basen är en kvadrat). Använd formeln  för att bestämma arean av en rektangel.
för att bestämma arean av en rektangel.
 för att bestämma arean av en rektangel.
för att bestämma arean av en rektangel.


4. Ersätt arean av basen med volymen av prismaformeln. Se till att ersätta variabeln  .
.
 .
.

5. Lös ekvationen för h  . Nu vet du höjden på ditt prisma.
. Nu vet du höjden på ditt prisma.
 . Nu vet du höjden på ditt prisma.
. Nu vet du höjden på ditt prisma. , du måste dividera varje sida med 16 om
, du måste dividera varje sida med 16 om  att räkna ut. Således:
att räkna ut. Således:

Så höjden på det rektangulära prismat är 4 meter.
Metod 2 av 4: Bestämning av höjden på ett triangulärt prisma med känd volym

1. Skriv ner formeln för volymen av ett prisma. Volymen av ett prisma kan hittas med hjälp av formeln  ,varigenom
,varigenom  är lika med prismats volym,
är lika med prismats volym,  är lika med arean av en bas, och
är lika med arean av en bas, och  är lika med prismats höjd.
är lika med prismats höjd.
 ,varigenom
,varigenom  är lika med prismats volym,
är lika med prismats volym,  är lika med arean av en bas, och
är lika med arean av en bas, och  är lika med prismats höjd.
är lika med prismats höjd. - Basen av ett prisma är en av dess kongruenta sidor. Basen på ett triangulärt prisma är en triangel. Sidorna är rektanglar.

2. Applicera volymen på formeln. Om du inte känner till volymen kan du inte använda den här metoden.
 ), din formel kommer att se ut så här:
), din formel kommer att se ut så här:

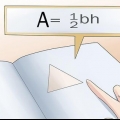
3. Hitta arean av basen. För att hitta arean behöver du veta längden på triangelns bas och triangelns höjd. Använd formeln  för att bestämma arean av en triangel.
för att bestämma arean av en triangel.
 för att bestämma arean av en triangel.
för att bestämma arean av en triangel.



4. Ersätt arean av basen med volymen av prismaformeln. Se till att ersätta variabeln  .
.
 .
.

5. Lös ekvationen för h  . Nu vet du höjden på ditt prisma.
. Nu vet du höjden på ditt prisma.
 . Nu vet du höjden på ditt prisma.
. Nu vet du höjden på ditt prisma. , du måste dividera varje sida med 42 för att avgöra
, du måste dividera varje sida med 42 för att avgöra  . Således:
. Således:

Metod 3 av 4: Hitta höjden på ett rektangulärt prisma med hjälp av dess area

1. Skriv formeln för arean av ett prisma. Formeln för arean av ett prisma är  , varigenom
, varigenom  är lika med ytan,
är lika med ytan,  är lika med arean av basen,
är lika med arean av basen,  är lika med basens omkrets, och
är lika med basens omkrets, och  är lika med prismats höjd.
är lika med prismats höjd.
 , varigenom
, varigenom  är lika med ytan,
är lika med ytan,  är lika med arean av basen,
är lika med arean av basen,  är lika med basens omkrets, och
är lika med basens omkrets, och  är lika med prismats höjd.
är lika med prismats höjd. - För att den här metoden ska fungera måste du känna till prismats yta, såväl som basens längd och bredd.

2. Ersätt arean av prismat i formeln. Om ytan är okänd kommer denna metod inte att fungera.


3. Hitta arean av basen. För att hitta arean måste du känna till basens längd och bredd (eller en sida, om basen är en kvadrat). Använd formeln  för att bestämma arean av en rektangel.
för att bestämma arean av en rektangel.
 för att bestämma arean av en rektangel.
för att bestämma arean av en rektangel.


4. Ersätt arean av basen med formeln för arean av ett prisma och förenkla. Se till att du fyller i brevet  .
.
 .
.


5. Bestäm basens omkrets. För att hitta omkretsen av en rektangel, addera längden på alla fyra sidorna tillsammans, eller multiplicera längden på en sida med 4 om det är en kvadrat.



6. Ersätt omkretsen av basen i formeln för arean av ett prisma. Se till att ersätta brevet  .
.
 .
.

7. Lös ekvationen för h  . Nu vet du höjden på ditt prisma.
. Nu vet du höjden på ditt prisma.
 . Nu vet du höjden på ditt prisma.
. Nu vet du höjden på ditt prisma. subtrahera först 32 från varje sida, dividera sedan varje sida med 20. Således:
subtrahera först 32 från varje sida, dividera sedan varje sida med 20. Således:



Metod 4 av 4: Bestäm höjden på ett triangulärt prisma med hjälp av dess area

1. Skriv formeln för arean av ett prisma. Formeln för arean av ett prisma är  , varigenom
, varigenom  är lika med ytan,
är lika med ytan,  är lika med arean av basen,
är lika med arean av basen,  är lika med basens omkrets, och
är lika med basens omkrets, och  är lika med prismats höjd.
är lika med prismats höjd.
 , varigenom
, varigenom  är lika med ytan,
är lika med ytan,  är lika med arean av basen,
är lika med arean av basen,  är lika med basens omkrets, och
är lika med basens omkrets, och  är lika med prismats höjd.
är lika med prismats höjd. - För att denna metod ska fungera måste arean av prismat vara känd, liksom arean av den triangulära basen och längden på alla tre sidor av basen.

2. Ersätt arean av prismat i formeln. Om ytan inte är känd kommer denna metod inte att fungera.


3. Hitta arean av basen. För att hitta arean behöver du veta längden på triangelns bas och triangelns höjd. Använd formeln  för att bestämma arean av en triangel.
för att bestämma arean av en triangel.
 för att bestämma arean av en triangel.
för att bestämma arean av en triangel.



4. Ersätt arean av basen i formeln för arean av ett prisma och förenkla. Ersättning för  .
.
 .
.


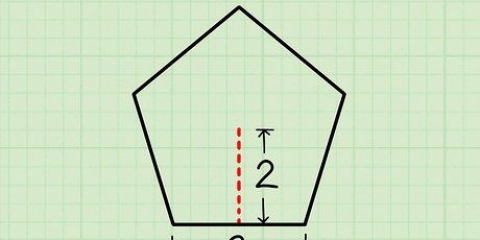
5. Bestäm basens omkrets. För att hitta omkretsen av en triangel, addera längden på alla tre sidor tillsammans.



6. Ersätt omkretsen av basen i formeln för arean av ett prisma. Se till att ersätta  .
.
 .
.

7. Lös ekvationen för h  . Nu vet du höjden på ditt prisma.
. Nu vet du höjden på ditt prisma.
 . Nu vet du höjden på ditt prisma.
. Nu vet du höjden på ditt prisma. , du måste först subtrahera 32 från varje sida och sedan dividera varje sida med 21. Således:
, du måste först subtrahera 32 från varje sida och sedan dividera varje sida med 21. Således:



Förnödenheter
- Penna/penna och papper eller miniräknare (valfritt)
Оцените, пожалуйста статью