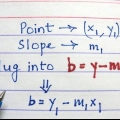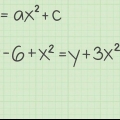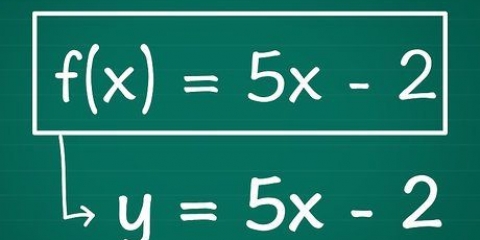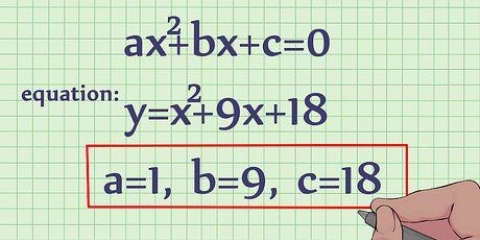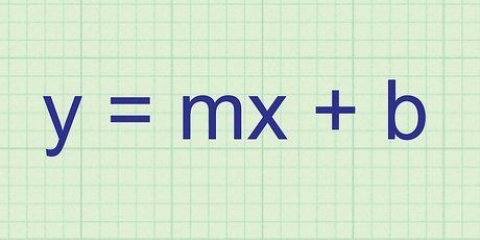Hitta ekvationen för en tangentlinje: 4 steg (med bilder)

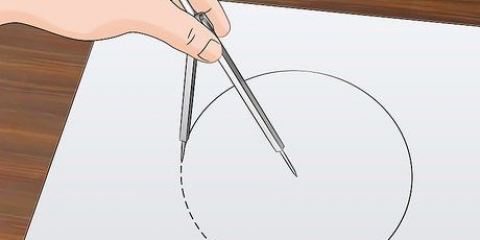
En tangent till en parabel eller kurva är en linje som bara vidrör kurvan vid en given punkt. För att hitta ekvationen för denna tangentlinje måste du beräkna kurvans lutning vid den punkten, vilket kräver några matematiska beräkningar. Du kan sedan skriva tangentlinjens ekvation i en punktlutningsform. Den här artikeln förklarar stegen att ta.

Steg

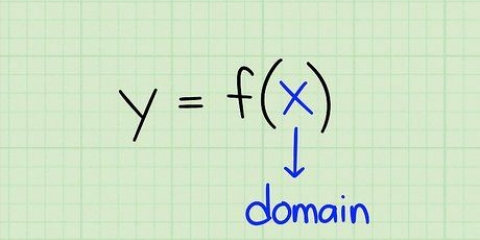
1. Ekvationen för en kurva kan uttryckas som en funktion. Hitta derivatan av denna funktion för att hitta ekvationen för lutningen på denna kurva.

Det enklaste sättet att skilja de flesta polynom är genom kedjeregeln. Multiplicera varje ekvation av funktionen med dess potens för att hitta koefficienten för den termen i derivatan, subtrahera sedan potensen med 1.
Exempel: För funktionen f(x) = x^3 + 2x^2 + 5x + 1 är derivatan f`(x) = 3x^2 + 4x + 5.
För f(x) = (2x+5)^10 + 2*(4x+3)^5, är derivatan f`(x) = 10*2*(2x+5)^9 + 2*5*4 *(4x+3)^4 = 20*(2x+5)^9 + 40*(4x+3)^4.

Bild med titeln Hitta ekvationen för en tangentlinje Steg 2

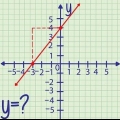
2. Om allt är bra ges koordinaterna där tangentlinjen möter kurvan. Plugga in x-värdet för denna punkt, i derivatfunktionen, för att hitta lutningen på kurvan vid den punkten.

För x = 2 är punkten på kurvan (2,27) eftersom f(2) = 2^3 + 2*2^2 + 5*2 + 1 = 27.

För f`(x) = 3x^2 + 4x + 5 är lutningen in (2,27) är f`(2) = 3(2)^2 + 4(2) + 5 = 25.

Bild med titeln Hitta ekvationen för en tangentlinje Steg 3

3. Denna lutning är också lutningen för tangentlinjen. Nu har du lutningen och punkten för denna linje, så du kan skriva linjens ekvation i punkt-lutningsform, eller y - y1 = m(x - x1).

I formen punkt-lutning, är m sluttningen och (x1,y1) är punktens koordinater. Så i det här exemplet blir ekvationen y - 27 = 25(x - 2).

4. Det kan också vara nödvändigt att konvertera denna ekvation till en annan form för att få det slutgiltiga svaret, om instruktionerna medföljer problemet kräver det.