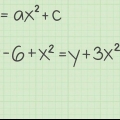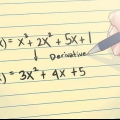Hitta derivatan av kvadratroten av x

Steg

Om du tog matte i skolan måste du ha lärt dig maktregeln för att bestämma derivatan av enkla funktioner. Men när funktionen innehåller en kvadratrot eller radikal, som t.ex $\sqrt{X}$ ${sqrt{x}}$ , då verkar maktens regel svår att tillämpa. Genom att använda en enkel substitution av exponenter blir det mycket enkelt att bestämma derivatan av en sådan funktion. Du kan sedan tillämpa samma substitution och använda kedjeregeln för att hitta derivatan av många andra funktioner med rötter.

Steg

Metod 1 av 3: Tillämpa maktregeln

1. Ta en ny titt på maktregeln för derivat. Den första regeln du förmodligen lärt dig för att hitta derivator är maktens regel. Denna regel säger att för en variabel

X

$X$ till makten av ett tal

a

$a$ , är derivatan och beräknas enligt följande:

$f (X) = X a$ ${displaystyle f(x)=x^{a}}$
$f sex (X) = a X^{a - 1}$ ${displaystyle f^{prime }(x)=ax^{a-1}}$
Ta en titt på följande exempelfunktioner och deras derivator:

om $f (X) = X 2$ ${displaystyle f(x)=x^{2}}$ , sedan $f sex (X) = 2 X$ ${displaystyle f^{prime }(x)=2x}$
om $f (X) = 3 X 2$ ${displaystyle f(x)=3x^{2}}$ , sedan $f sex (X) = 2 * 3 X = 6 X$ ${displaystyle f^{prime }(x)=2*3x=6x}$
om $f (X) = X 3$ ${displaystyle f(x)=x^{3}}$ , sedan $f sex (X) = 3 X^{2}$ ${displaystyle f^{prime }(x)=3x^{2}}$
om $f (X) = \frac{1}{2} X^{4}$ ${displaystyle f(x)={frac {1}{2}}x^{4}}$ , sedan $f sex (X) = 4 * \frac{1}{2} X^{3} = 2 X^{3}$ ${displaystyle f^{prime }(x)=4*{frac {1}{2}}x^{3}=2x^{3}}$

Bild med titeln Differentiate the Square Root of X Steg 2

2. Skriv om kvadratroten som exponent. För att hitta derivatan av en kvadratrotsfunktion, kom ihåg att kvadratroten av ett tal eller en variabel också kan skrivas som en exponent. Termen under radikalen skrivs som en bas, och höjs till makten 1/2. Termen används också som en exponent för kvadratroten. Titta igenom följande exempel:

\sqrt{X} = X^{\frac{1}{2}}

${displaystyle {sqrt {x}}=x^{frac {1}{2}}}$

\sqrt{4} = 4^{\frac{1}{2}}

${displaystyle {sqrt {4}}=4^{frac {1}{2}}}$

\sqrt{3 X} = (3 X)^{\frac{1}{2}}

${displaystyle {sqrt {3x}}=(3x)^{frac {1}{2}}}$

Bild med titeln Differentiate the Square Root of X Steg 3

3. Tillämpa maktens regel. Om funktionen är den enklaste kvadratroten,

f (X) = \sqrt{X}

${displaystyle f(x)={sqrt {x}}}$ , använd sedan potensregeln enligt följande för att hitta derivatan:

f (X) = \sqrt{X}

${displaystyle f(x)={sqrt {x}} }$ (Skriv ner den ursprungliga funktionen.)

f (X) = X (\frac{1}{2})

${displaystyle f(x)=x^{({frac {1}{2}})} }$ (Skriv om roten som en exponent.)

f sex (X) = \frac{1}{2} X^{(\frac{1}{2} - 1)}

${displaystyle f^{prime }(x)={frac {1}{2}}x^{({frac {1}{2}}-1)} }$ (Hitta derivatan med hjälp av potensregeln.)

f sex (X) = \frac{1}{2} X^{(- \frac{1}{2})}

${displaystyle f^{prime }(x)={frac {1}{2}}x^{(-{frac {1}{2}})} }$ (Förenkla exponenten.)

Bild med titeln Differentiera kvadratroten av X Steg 4

4. Förenkla resultatet. I detta skede bör du veta att en negativ exponent betyder att du tar inversen av vad som skulle vara talet med den positiva exponenten. Exponenten för

- \frac{1}{2}

${displaystyle -{frac {1}{2}}}$ betyder att kvadratroten av basen blir nämnaren för ett bråk.

Om vi fortsätter med kvadratroten av funktionen x ovanifrån, kan derivatan förenklas på följande sätt:

f sex (X) = \frac{1}{2} X^{- \frac{1}{2}}

${displaystyle f^{prime }(x)={frac {1}{2}}x^{-{frac {1}{2}}}}$

f sex (X) = \frac{1}{2} * \frac{1}{\sqrt{X}}

${displaystyle f^{prime }(x)={frac {1}{2}}*{frac {1}{sqrt {x}}}}$

f sex (X) = 12 \sqrt{X}

${displaystyle f^{prime }(x)={frac {1}{2{sqrt {x}}}}}$

Metod 2 av 3: Tillämpa kedjeregeln för kvadratrotsfunktioner

Bild med titeln Differentiera kvadratroten av X Steg 5

1. Revidera kedjeregeln för funktioner. Kedjeregeln är en regel för derivator som du använder när den ursprungliga funktionen kombinerar en funktion i en annan funktion. Kedjeregeln säger det, för två funktioner

f (X)

$f(x)$ och

g (X)

${displaystyle g(x)}$ , derivatan av kombinationen av de två funktionerna kan hittas enligt följande:

om $y = f (g (X))$ ${displaystyle y=f(g(x))}$ , sedan $y sex = f^{sex} (g) * g^{sex} (X)$ ${displaystyle y^{prime }=f^{prime }(g)*g^{prime }(x)}$ .

Bild med titeln Differentiera kvadratroten av X Steg 6

2. Definiera kedjeregelfunktionerna. Att använda kedjeregeln kräver att du först definierar de två funktionerna som utgör din kombinerade funktion. För kvadratrotsfunktioner är den yttersta funktionen

f (g)

${displaystyle f(g)}$ kvadratrotsfunktionen och den innersta funktionen

g (X)

${displaystyle g(x)}$ funktionen under radikalen.

Till exempel: anta att du har derivatan av

\sqrt{3 X + 2}

${displaystyle {sqrt {3x+2}}}$ vill hitta. Definiera sedan de två delarna enligt följande:

f (g) = \sqrt{g} = g^{\frac{1}{2}}

${displaystyle f(g)={sqrt {g}}=g^{frac {1}{2}}}$

g (X) = (3 X + 2)

${displaystyle g(x)=(3x+2)}$

Bild med titeln Differentiera kvadratroten av X Steg 7

3. Hitta derivatan av de två funktionerna. För att tillämpa kedjeregeln på kvadratroten av en funktion måste du först hitta derivatan av den allmänna kvadratrotsfunktionen:

f (g) = \sqrt{g} = g^{\frac{1}{2}}

${displaystyle f(g)={sqrt {g}}=g^{frac {1}{2}}}$

f sex (g) = \frac{1}{2} g^{- \frac{1}{2}}

${displaystyle f^{prime }(g)={frac {1}{2}}g^{-{frac {1}{2}}}}$

f sex (g) = 12 \sqrt{g}

${displaystyle f^{prime }(g)={frac {1}{2{sqrt {g}}}}}$

Bestäm sedan derivatan av den andra funktionen:

g (X) = (3 X + 2)

${displaystyle g(x)=(3x+2)}$

g sex (X) = 3

${displaystyle g^{prime }(x)=3}$

Bild med titeln Differentiate the Square Root of X Steg 8

4. Kombinera funktionerna i kedjeregeln. Kedjeregeln är

y sex = f^{sex} (g) * g^{sex} (X)

${displaystyle y^{prime }=f^{prime }(g)*g^{prime }(x)}$ . Kombinera derivaten enligt följande:

y sex = 12 \sqrt{g} * 3

${displaystyle y^{prime }={frac {1}{2{sqrt {g}}}}*3}$

y sex = 12 \sqrt{(3 X + 2} * 3

${displaystyle y^{prime }={frac {1}{2{sqrt {(3x+2}}}}*3}$

y sex = 32 \sqrt{(3 X + 2}

${displaystyle y^{prime }={frac {3}{2{sqrt {(3x+2}}}}}$

Metod 3 av 3: Hitta derivator av rotfunktioner snabbt

Bild med titeln Differentiera kvadratroten av X Steg 9

1. Bestäm derivator av en kvadratrotsfunktion med en snabbmetod. När du vill hitta derivatan av kvadratroten av en variabel eller en funktion kan du tillämpa en enkel regel: derivatan kommer alltid att vara derivatan av talet under radikalen, dividerat med dubbla den ursprungliga kvadratroten. Symboliskt kan detta representeras som:

om $f (X) = \sqrt{du}$ ${displaystyle f(x)={sqrt {u}}}$ , sedan $f sex (X) = du sex 2 \sqrt{du}$ ${displaystyle f^{prime }(x)={frac {u^{prime }}{2{sqrt {u}}}}}$

Bild med titeln Differentiate the Square Root of X Steg 10

2. Hitta derivatan av talet under radikalen. Detta är ett tal eller en funktion under kvadratrottecknet. För att använda denna snabba metod, hitta bara derivatan av talet under radikalen. Kolla in följande exempel:

I funktionen

\sqrt{5 X + 2}

${displaystyle {sqrt {5x+2}}}$ , är rotnumret

(5 X + 2)

${displaystyle (5x+2)}$ . Derivaten är

5

$5$ .

I funktionen

\sqrt{3 X} 4

${displaystyle {sqrt {3x^{4}}}}$ , är rotnumret

3 X 4

${displaystyle 3x^{4}}$ . Derivaten är

12 X 3

${displaystyle 12x^{3}}$ .

I funktionen

\sqrt{s i n (X)}

${displaystyle {sqrt {sin(x)}}}$ , är rotnumret

synd (X)

${displaystyle sin(x)}$ . Derivaten är

\cos (X)

${displaystyle cos(x)}$ .

Bild med titeln Differentiera kvadratroten av X Steg 11

3. Skriv derivatan av rottalet som täljaren för ett bråk. Derivatan av en kvadratrotsfunktion kommer att innehålla en bråkdel. Täljaren för detta bråk är derivatan av rottalet. Så i exempelfunktionerna ovan kommer den första delen av derivatan att se ut så här:

f (X) = \sqrt{5 X + 2}

${displaystyle f(x)={sqrt {5x+2}}}$ , sedan

f sex (X) = \frac{5}{nämnare}

${displaystyle f^{prime }(x)={frac {5}{text{nämnare}}}}$

f (X) = \sqrt{3 X} 4

${displaystyle f(x)={sqrt {3x^{4}}}}$ , sedan

f sex (X) = 12 X 3 nämnare

${displaystyle f^{prime }(x)={frac {12x^{3}}{text{nämnare}}}}$

f (X) = \sqrt{synd (X)}

${displaystyle f(x)={sqrt {sin(x)}}}$ , sedan

f sex (X) = \cos (X) nämnare

${displaystyle f^{prime }(x)={frac {cos(x)}{text{nämnare}}}}$

Bild med titeln Differentiate the Square Root of X Steg 12

4. Skriv nämnaren som dubbelt den ursprungliga kvadratroten. Med denna snabba metod är nämnaren två gånger den ursprungliga kvadratrotsfunktionen. Så i de tre exempelfunktionerna ovan är nämnarna för derivatorna:

f (X) = \sqrt{5 X + 2}

${displaystyle f(x)={sqrt {5x+2}}}$ , sedan

f sex (X) = disken 2 \sqrt{5 X + 2}

${displaystyle f^{prime }(x)={frac {text{counter}}{2{sqrt {5x+2}}}}}$

f (X) = \sqrt{3 X} 4

${displaystyle f(x)={sqrt {3x^{4}}}}$ , sedan

f sex (X) = disken 2 \sqrt{3 X} 4

${displaystyle f^{prime }(x)={frac {text{counter}}{2{sqrt {3x^{4}}}}}}}$

f (X) = \sqrt{synd (X)}

${displaystyle f(x)={sqrt {sin(x)}}}$ , sedan

f sex (X) = disken 2 \sqrt{synd (X)}

${displaystyle f^{prime }(x)={frac {text{counter}}{2{sqrt {sin(x)}}}}}$

Bild med titeln Differentiate the Square Root of X Steg 13

5. Kombinera täljaren och nämnaren för att hitta derivatan. Sätt ihop de två halvorna av bråket och resultatet blir derivatan av den ursprungliga funktionen.