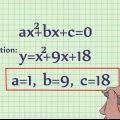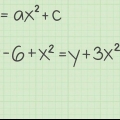I exemplet ovan, om du dividerar båda sidor med 2, 2x = 6, får du 2/2 x = 6/2, eller x = 3. Detta är x-skärningspunkten för ekvationen 2x + 3y = 6. Du kan använda samma steg för ekvationer av formen ax^2 + by^2 = c. I det här fallet, om du anger 0 för y, får du x^2 = c/a, och efter att du hittat värdet till höger om likhetstecknet måste du hitta roten till x-kvadrat. Detta ger dig 2 värden, 1 positivt och 1 negativt, som summerar till 0. 

Faktorering är att dela upp en andragradsekvation i 2 enklare algebraiska uttryck som, när de multipliceras tillsammans, producerar andragradsekvationen. Ofta kan värdena för a och c vara nyckeln till att hitta rätt faktorer. Eftersom 2 gånger 5 är lika med 10, är det absoluta värdet av c, och eftersom det absoluta värdet av b är mindre än det för c, är 2 och 5 förmodligen de numeriska komponenterna av de korrekta faktorerna. Eftersom 5 minus 2 är lika med 3 är de korrekta faktorerna x + 5 och x - 2. Om du fyller i faktorerna för andragradsekvationen, (x + 5)(x - 2) = 0, är 2x skärningspunkterna -5 (-5 + 5 = 0) och 2 (2 - 2 = 0). Om du använder den kvadratiska formeln, infoga värdena för a, b och c från den kvadratiska formeln i formeln (-b + eller - W (b^2 - 4 ac))/2a (där W är kvadraten root ) för att hitta värdet eller värdena för x. Om du kopplar in värdena 1, 3 och -10 i denna ekvation får du (-3 + eller - W (3^2 - 4(1)(-10)))/2(1). Värdet inom W-parenteserna kommer ut till 9 -(-40) eller 9+40, vilket är 49, så ekvationen kommer ut till (-3 + eller - 7)/2, vilket leder till (-3 + 7 ) /2 eller 4/2, vilket är 2, och (-3 -7)/2 eller -10/2, vilket är -5. Till skillnad från de enkla 2-variabelekvationerna som beskrivs i föregående avsnitt, ritas andragradsekvationer på en koordinatgraf som en parabel (en krökt linje som liknar en "DU" eller "V") istället för en rak linje. Andragradsekvationer kan inte ha någon x-skärning, 1 x skärningspunkt eller 2 x skärningspunkt.
Hitta skärningspunkten med x-axeln
I algebra har tvådimensionella grafer med koordinater en horisontell axel eller x-axel och en vertikal axel eller y-axel. De platser där linjer som representerar ett värdeintervall skär dessa axlar kallas skärningspunkter. Y-skärningen är där linjen skär y-axeln och x-skärningen är där linjen skär x-axeln. Att hitta x-skärningspunkten med algebra kan vara enkelt eller komplicerat, beroende på om ekvationen bara har 2 variabler eller är kvadratisk. Stegen nedan visar hur det fungerar för båda typerna av ekvationer.
Steg
Metod 1 av 2: Enkla ekvationer med 2 variabler

1. Byt ut värdet på y med 0. Vid den punkt där värdelinjen korsar den horisontella axeln har y värdet 0.
- I exemplets ekvation, om du ersätter 2x + 3y = 6, y med 0, ändras ekvationen till 2x + 3(0) = 6, så i princip bara 2x = 6.

2. Hitta lösningen för x. Detta innebär vanligtvis att man dividerar båda sidor av ekvationen med koefficienten för x för att ge den värdet 1.
Metod 2 av 2: För andragradsekvationer

1. Sätt ekvationen i formen ax^2 + bx + c = 0. Detta är standardformen för att skriva en andragradsekvation, där a är koefficienten för x-kvadrat, b är koefficienten för x och c är ett rent numeriskt värde.
- För exemplet i det här avsnittet använder vi ekvationen x^2 +3x - 10 = 0.

2. Lös ekvationen för x. Det finns flera sätt att lösa en andragradsekvation. De 2 vi har att göra med här är factoring och använder den kvadratiska formeln.
Tips
- Om i exemplet jämförelse nedan "Enkla ekvationer med 2 variabler" Om du anger en 0 för x istället för y kan du ta reda på värdet på y-skärningen.
"Hitta skärningspunkten med x-axeln"
Оцените, пожалуйста статью