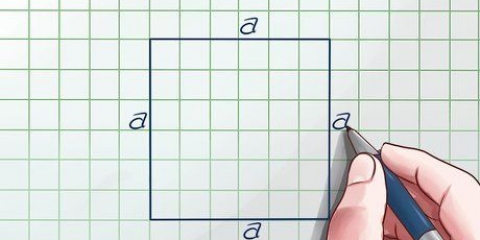
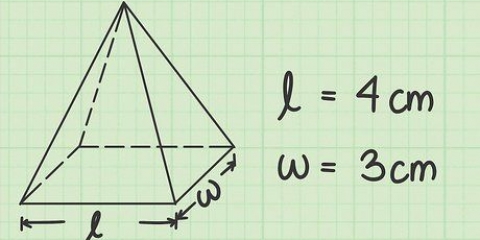Eftersom alla fyra sidor av en kvadrat är lika, kommer kvadratens "längd" att vara identisk med dess "bredd". I det här fallet behöver du bara mäta på ett sätt. 
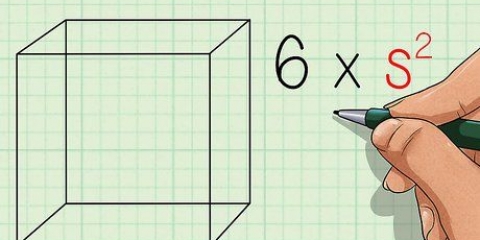
Anta till exempel att du har ett rektangulärt område med en längd på 4 centimeter och en bredd på 3 centimeter. I detta fall är rektangelns area 4 × 3=12 kvadratcentimeter. När det gäller kvadrater, eftersom alla fyra sidorna är lika, kan du helt enkelt mäta en sida och multiplicera den med sig själv (kallas även "kvadrat" eller höja potensen till andra potensen) för att beräkna arean i kvadratcentimeter. 

Så om du har en bas med en längd på 4 centimeter och motsvarande höjd är 3 centimeter, blir resultatet 2 x 3 = 6 kvadratcentimeter. 
Så om längden på en sida är 5 centimeter och höjden är 4 centimeter, är den resulterande ytan 5 x 4 = 20 centimeter. 
Så om långsidan av din trapets är 6 centimeter, kortsidan är 4 centimeter och höjden är 5 centimeter, blir resultatet ½ x 5 x (6 + 4) = 25 cm. 
Så om du har en hexagon med 6 lika sidor på 4 centimeter vardera (vilket betyder P=6 x 4=24) och en apotem på 3,5 centimeter, då är beräkningen ½ x 24 x 3,5=42 cm. 
Så, om du har en vanlig oktagon med en längd på 4 centimeter, beräknar du (2 x16) x (1 + 1,4) = 32 x 2,4 = 76,8 cm. 

Till exempel 400 kvadratfot=400 x 144=57600 tum. 
På samma sätt är 1 kvadratmeter lika med 10.000 kvadratcentimeter, och att en kvadratkilometer är lika med 10.000.000.000 kvadratcentimeter. Så en kvadratkilometer = 10.000.000.000 kvadratcentimeter x 0,155=1.550.003.100 tum.
Beräkna kvadratcentimeter
Att bestämma kvadratcentimeter (även skrivet som cm) i ett tvådimensionellt utrymme är vanligtvis ganska enkelt. I de enklaste fallen, som en kvadrat eller rektangel, kan arean i kvadratcentimeter beräknas med hjälp av ekvationen längd × bredd. Arean av andra former (cirklar, trianglar, etc.) kan beräknas via ett antal specialiserade matematiska ekvationer. Om det behövs kan du också enkelt konvertera till kvadrattum från kvadratfot eller kvadratcentimeter.
Steg
Metod 1 av 3: Bestämma kvadratcentimeter i en kvadrat eller rektangel

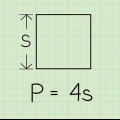
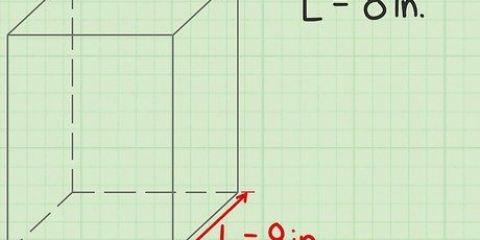
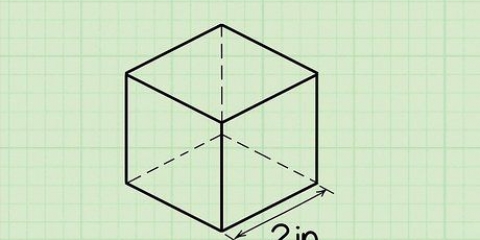
1. Särskild längd av ytan som ska mätas. Kvadrater och rektanglar har fyra raka sidor. När det gäller rektanglar är de motsatta sidorna lika långa medan i fallet med kvadrater är alla fyra sidorna lika långa. Mät en av sidorna av kvadraten eller den längsta sidan av rektangeln för längden.

2. Särskild bredd av ytan som ska mätas. Sedan mäter du en av sidorna som ligger i anslutning till sidan du just mätt. Denna sida ska skära den första sidan i 90 graders vinkel. Detta andra mått är bredden på kvadraten eller rektangeln.

3. Multiplicera längd × bredd. Multiplicera längden och bredden på din kvadrat eller rektangel för att hitta arean i kvadratcentimeter.
Metod 2 av 3: Bestäm området för andra former

1. Hitta arean av en cirkel med ekvationen area=pi × r. För att beräkna arean av en cirkel i kvadratcentimeter behöver du bara veta avståndet från cirkelns mitt till kanten i centimeter. Detta avstånd kallas Stråle av cirkeln. När du känner till detta värde, ersätt det med `r` i ekvationen ovan. Multiplicera radien med sig själv, sedan med den matematiska konstanten pi (3,1415926...) för att bestämma antalet kvadratcentimeter inom cirkeln.
- Så en cirkel med en radie på 4 centimeter har en area på 50,27 kvadratcentimeter, produkten av 3,14 x 16.

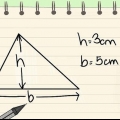
2. Hitta arean av en triangel med hjälp av ekvationen Area=1/2 b × h i kvadratcentimeter. Arean av en triangel erhålls genom att multiplicera basen (`b`) med höjden (`h`). Basen av en triangel är längden på en av dess sidor, medan dess höjd är avståndet från "basen" till det motsatta hörnet, mätt i en vinkel på 90 grader från "basen". Arean av en triangel kan beräknas med dess bas och höjd, för var och en av dess tre sidor och den motsatta vinkeln.

3. Hitta arean av ett parallellogram med hjälp av ekvationen Area=b × h. Parallelogram liknar rektanglar; den enda skillnaden är att deras vinklar inte nödvändigtvis är 90 grader. Sättet att beräkna arean i kvadratcentimeter av ett parallellogram liknar sättet att beräkna det för en rektangel - multiplicera bara basen av ett parallellogram med dess höjd och se till att båda måtten är i centimeter. Basen är längden på en av sidorna medan höjden är avståndet från basen till motsatt sida mätt i rät vinkel.

4. Hitta arean av en trapets med ekvationen Area=1/2 × h × (B + b). En trapets är en fyrsidig form med två parallella sidor och två icke-parallella sidor. För att beräkna arean i kvadratcentimeter behöver du känna till tre mått (i centimeter): längden på den längsta parallella sidan (`B`), längden på den kortare parallella sidan (`b`) och höjden ( ` h`) för trapetsen (avståndet mellan de två parallella sidorna, mätt i rät vinkel). Addera längderna på de två sidorna tillsammans, multiplicera det med höjden och halvera sedan resultatet för att hitta arean på trapetsen.

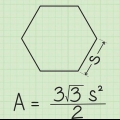
5. Hitta arean av en hexagon med ekvationen Area=½ × P × a. Denna formel fungerar för alla vanliga hexagoner, vilket betyder att den har 6 lika sidor och 6 lika vinklar. sid representerar omkretsen eller 6 gånger längden på en sida (6 x s) för en vanlig hexagon. a representerar apotem - längden från mitten av hexagonen till mitten av ena sidan (dvs halvvägs mellan två valfria hörn). Multiplicera detta och halvera resultatet för att hitta arean.

6. Hitta arean av en oktagon med ekvationsarean=2a² × (1 + √2). För en vanlig oktagon (med 8 lika sidor och 8 lika vinklar) behöver du bara veta längden på en sida (`a` i formeln) för att beräkna arean. Använd det måttet i formeln och du har ditt resultat.
Metod 3 av 3: Omvandlingar till kvadrattum

1. Konvertera måtten till tum innan du gör beräkningar. För att få ditt slutliga svar i kvadrattum är det bäst att ha alla mått som behövs för formeln (som längd, höjd eller apotem) i tum. Så om sidorna på din kvadrat är 1 fot vardera, konvertera detta till 12 tum innan du beräknar arean. Här är omvandlingsfaktorerna för vanliga måttenheter:
- 1 fot = 12 tum
- 1 yard = 36 tum
- 1 centimeter=0,3937 tum
- 1 meter=39,3701 tum
- 1 millimeter=0,0394 tum

2. Multiplicera med 144 för att konvertera från kvadratfot till kvadrattum. 1 kvadratfot är bokstavligen 1 fot i kvadrat (eller 1 fot gånger 1 fot); Detta är samma sak som 12 tum gånger 12 tum, eller 144 kvadrattum. Så om du har en yta i kvadratfot, multiplicera den med 144 för att få arean i kvadrattum.

3. Multiplicera med 0,155 för att omvandla kvadratcentimeter till kvadrattum. 1 centimeter motsvarar ungefär 0,394 tum och 0,394 kvadrat (0,394 x 0,394) i är lika med 0,155. Så om du behöver konvertera en yta på 250 cm till tum multiplicerar du 250 med 0,155 och du får 38,75 tum.
"Beräkna kvadratcentimeter"
Оцените, пожалуйста статью