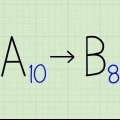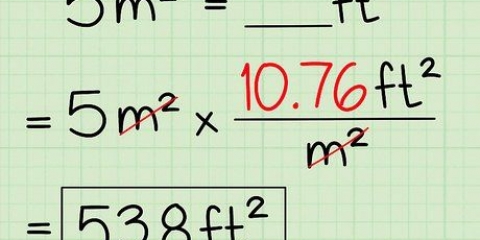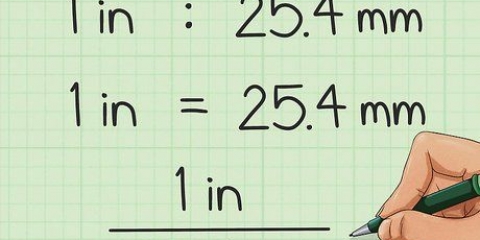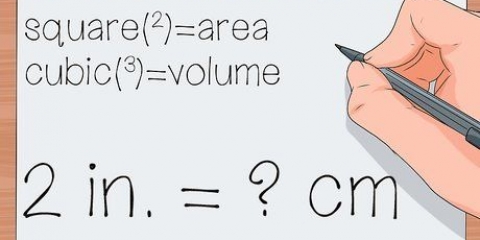16 = 1.048.576 16 = 65.536 16 = 4.096 16 = 256 16 = 16 Om decimaltalet du konverterar är större än 1.048.576, beräkna sedan de högre potenserna av 16 och lägg till den i listan. 
Till exempel om du 495 konvertera till hexadecimal och välj sedan 256 från listan ovan. 
I vårt exempel är 495 ÷ 256 = 1.93... , men vi är bara intresserade av hela numret 1. Ditt svar är den första siffran i det hexadecimala talet. I det här fallet, eftersom vi har dividerat med 256, är 1:an talet i stället för "256-en." 
Multiplicera ditt sista svar med divisor. I vårt exempel är 1 x 256 = 256. (Med andra ord, 1:an i vårt hexadecimala tal representerar 256:an med basen 10). Subtrahera ditt svar från utdelningen. 495 - 256 = 239. 
239 ÷ 16 = 14. Återigen ignorerar vi alla decimaler. Detta är den andra siffran i vårt hexadecimala nummer, den "16-och." Alla tal från 0 till 15 kan representeras som en enda hexadecimal siffra. Vi konverterar till rätt notation i slutet av denna metod. 
14 x 16 = 224. 239 - 224 = 15, så resten är 15. 
Den sista "figur" av vårt hexadecimala tal är 15, i stället för "enheter." 
Siffrorna 0 till 9 förblir desamma. 10 = A; 11 = B; 12 = C; 13 = D; 14 = E; 15 = F I vårt exempel slutar vi med siffrorna (1)(14)(15). I korrekt notation blir detta det hexadecimala talet 1EF. 
1EF → (1)(14)(15) Från höger till vänster är 15 i 16 = 1:a position. 15 x 1 = 15. Nästa siffra från vänster är i 16 = 16:e positionen. 14 x 16 = 224. Nästa siffra är i 16 = 256:e positionen. 1 x 256 = 256. Vi lägger ihop dem alla, 256 + 224 + 15 = 495, vårt ursprungliga nummer. 

För att hitta resten, multiplicera svaret med divisor och subtrahera sedan resultatet från utdelningen. I vårt exempel, 317.547 - (19.846 x 16) = 11. Konvertera siffran till hexadecimalt format med hjälp av tabellen för småtalskonvertering överst på den här artikelsidan. 11 varv B i vårt exempel. 
I vårt exempel, 19.846 / 16 = 1.240. rest = 19.846 - (1.240 x 16) = 6. Detta är den näst sista siffran i vårt hexadecimala tal. 
Ta den sista kvoten och dividera den igen med 16. 1.240 / 16 = 77 återstoden 8. 77 / 16 = 4 återstoden 13 = d. 4 < 16, alltså 4 är den första siffran. 
Vårt sista svar är 4D86B. För att kontrollera ditt arbete, konvertera varje siffra tillbaka till decimaltalet, multiplicerat med 16 potenser, och addera resultaten tillsammans. (4 x 16) + (13 x 16) + (8 x 16) + (6 x 16) + (11 x 1) = 317.547, vårt ursprungliga decimaltal.
Konvertera från decimal till hexadecimal
Hexadecimal är ett talsystem med basen sexton. Det betyder att det finns 16 symboler för att indikera ett nummer, med A, B, C, D, E och F läggs till de vanliga tio siffrorna. Att konvertera från decimal till hexadecimal är svårare än tvärtom. Ta dig tid att lära dig detta eftersom det är lättare att undvika misstag när du väl förstår varför konverteringen fungerar.
Konverteringar med små antal
| Decimal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Hexadecimal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | a | B | C | d | E | f |
Steg
Metod 1 av 2: Intuitiv metod

1. Använd den här metoden om du är ny på hexadecimala tal. Av de två tillvägagångssätten i den här artikeln är detta det enklaste för de flesta att följa. Om du redan är bekant med de olika baserna, prova den snabbare metod som anges nedan.
- Om du är helt obekant med hexadecimala tal, lär dig de grundläggande begreppen först.

2. Skriv ner potenserna för 16. Varje siffra i det hexadecimala systemet representerar en annan potens av 16, precis som en decimalsiffra är en potens av 10. Den här listan med 16 potenser kommer att vara praktisk vid konvertering:

3. Hitta den högsta potensen av 16 som passar inom decimaltalet. Skriv ner det decimaltal du vill konvertera. Använd listan ovan som referens. Hitta den högsta potensen av 16 som är mindre än decimaltalet.

4. Dividera decimaltalet med denna potens av 16. Stanna vid hela talet och ignorera varje siffra efter decimalkomma i svaret.

5. Hitta resten. Detta talar om vad som är kvar av decimaltalet som ska konverteras. Så här kan du räkna ut det, precis som med en lång division:

6. Dela resten med nästa högre potens av 16. Använd din lista över potenser på 16 igen som referens. Fortsätt så här till minst 16. Dividera resten med det värdet för att hitta nästa siffra i ditt hexadecimala tal. (Om resten är mindre än detta nummer är nästa siffra 0.)

7. Bestäm resten igen. Som tidigare, multiplicera svaret med divisor och subtrahera det från utdelningen. Detta är resten som fortfarande behöver konverteras.

8. Upprepa tills du har en återstod på mindre än 16. När återstoden är 0 till 15 kan den uttryckas med en enda hexadecimal siffra. Skriv detta som den sista siffran.

9. Skriv ditt svar i rätt notation. Du vet nu vad alla siffror i ditt hexadecimala nummer är. Men hittills har vi bara skrivit dem i bas tio. För att skriva varje siffra i rätt hexadecimal notation, konvertera dem med hjälp av denna guide:

10. Kontrollera ditt arbete. Det är enkelt att kontrollera ditt svar när du förstår hur hexadecimala tal fungerar. Konvertera varje siffra tillbaka till decimalform och multiplicera dem med 16:e potens för den baspositionen. Här är vad vi behöver göra för vårt exempel:
Metod 2 av 2: Snabb metod (med vila)

1. Dividera decimaltalet med 16. Behandla denna division som en heltalsdivision. Du stannar med andra ord vid ett svar med ett heltal, istället för att räkna ut decimaltalen.
- Låt oss vara lite mer ambitiösa om det här exemplet och decimaltalet 317.547 konvertera. Beräkna 317.547 ÷ 16 = 19.846, och ignorera decimalerna.

2. Skriv resten i hexadecimal notation. Nu när du har dividerat talet med 16, är resten den del som inte längre passar 16:ornas eller högre position. Därför måste resten komma till läget för enheterna, det sista siffran i det hexadecimala talet.

3. Upprepa denna process med kvoten. Du konverterade resten till en hexadecimal siffra. För att fortsätta konvertera kvoten, dividera den igen med 16. Resten är den näst sista siffran i det hexadecimala talet. Detta fungerar med samma logik som ovan: det ursprungliga talet delas nu med (16 x 16 =) 256, så resten är den del av talet som passar 256:ornas position. Vi känner till enheterna sedan tidigare, resten måste vara på 16:ornas plats.

4. Upprepa tills du får en kvot mindre än 16. Glöm inte att konvertera en rest från 10 till 15 i hexadecimalt format. Notera eventuell vila längs vägen. Den sista kvoten (mindre än 16) är den första siffran i ditt nummer. Vi fortsätter med exemplet:

5. Avsluta numret. Som nämnts tidigare bestämmer du varje siffra i det hexadecimala talet från höger till vänster. Kontrollera ditt arbete för att se till att du skrev dem i rätt ordning.
Tips
- För att undvika förvirring när du använder de olika numeriska systemen kan du skriva basen som ett abonnemang. Till exempel 51210 är då "512 med bas 10," ett vanligt decimaltal. 51216 betyder att "512 med bas 16," motsvarar decimaltalet 1.29810.
"Konvertera från decimal till hexadecimal"
Оцените, пожалуйста статью