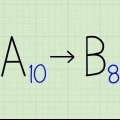Det binär (bas 2) nummersystem har två möjliga värden, vanligtvis representerade som 0 eller 1, för varje position i ett tal. Skillnaden med decimal- (bas 10) nummersystem är att det finns tio möjliga värden (0,1,2,3,4,5,6,7,8 eller 9) för varje position.
För att undvika förvirring vid användning av olika nummersystem kan basen för ett nummer anges genom att teckna det efter numret.Till exempel kan det binära talet 10011100 skrivas till bas 2 genom att skriva det som 100111002.Decimaltalet 156 kan skrivas som 15610 eller i sin helhet som "hundra och femtiosex, bas 10".
Eftersom det binära systemet är datorernas maskinspråk måste seriösa programmerare till fullo förstå hur man konverterar binära tal till decimaltal.Att konvertera i motsatt riktning, från decimal till binär, är ofta svårare att lära sig först.
Obs: Detta handlar ENDAST om beräkningar och inte ASCII-översättningar.
Steg
Metod 1 av 2: Positionssystemmetod
1. I det här exemplet kommer vi att använda det binära numret 100110112 konvertera till decimal. Lista två potenser från höger till vänster. Börja med 2, detta har värdet "1".Multiplicera exponenterna med 1 för varje potens.Stoppa när antalet element i listan är lika med antalet siffror i det binära talet. Numret i exemplet, 10011011, har 8 siffror, så listan kommer att se ut så här: 128, 64, 32, 16, 8, 4, 2, 1
2. Skriv det binära talet under listan.
3. Anslut med linjer de binära talen med två potenser. Rita linjer som förbinder varje binär siffra med motsvarande andra potens ovanför den.Börja vid den första binära siffran, från höger, och fortsätt tills du har kopplat alla binära siffror och potenserna.
4. Gå igenom alla siffror i det binära numret. Om talet är en 1, skriv motsvarande andra potens under linjen, direkt under talet.Om talet är en 0, skriv en 0 under linjen.
5. Lägg ihop siffrorna under linjen. Summan bör vara 155. Detta är decimalmotsvarigheten till det binära talet 10011011.Eller, skrivet med basen i subscript:
6. Om du upprepar den här metoden ofta kommer du att upptäcka att du minns två potenser bättre, så du kan hoppa över steg 1.
Metod 2 av 2: Fördubblingsmetod
1. Denna metod använder inte befogenheter. Därför passar det bättre om du vill konvertera större tal utantill, då du bara behöver komma ihåg delsumman.
2. Börja med siffran längst till vänster om det givna binära talet. För varje efterföljande nummer från vänster till höger, dubbla föregående summa och lägg till det till det aktuella numret. Till exempel för att ange numret 10110012 för att konvertera till decimal tar vi följande steg:
3. 1011001 → 0 * 2 + 1 = 1
4. 1011001 → 1 * 2 + 0 = 2
5. 1011001 → 2 * 2 + 1 = 5
6. 1011001 → 5 * 2 + 1 = 11
7. 1011001 → 11 * 2 + 0 = 22
8. 1011001 → 22 * 2 + 0 = 44
9. 1011001 → 44 * 2 + 1 = 8910
10. Liksom positionssystemmetoden kan denna metod modifieras för att konvertera från vilket talsystem som helst till ett decimaltal.Dubbling används här eftersom basen är två. Om det givna talet har en annan bas, använd den istället för 2. Till exempel, om talet har basen 37, byt *2 mot *37. Resultatet kommer alltid att vara ett decimaltal (bas 10). :)
Tips
- Öva mycket. Prova de binära talen 110100012, 110012, och 111100012.Deras decimalekvivalenter är 20910, 2510, och 24110.
- Kalkylatorn som följer med Microsoft Windows kan också göra denna konvertering åt dig, men om du är programmerare är det bättre att du har en god förståelse för hur denna konvertering fungerar. Alternativen för denna kalkylator kan hittas genom "Se" menyn och sedan "Vetenskaplig" (eller "programmerare"). Med Linux kan du använda galkulator.
Varningar
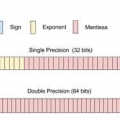
- Detta kan användas till osignerad binär (endast positiva tal), men inte för tecken, flyttal eller fast punkt.
"Konvertera ett binärt tal till ett decimaltal"