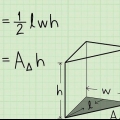
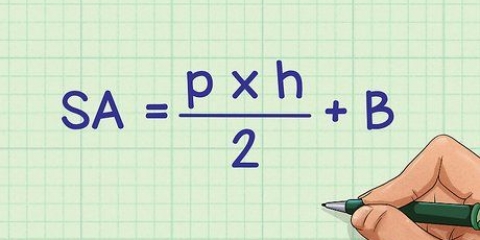A = 1/2(o)(h) A = 1/2(2)(4) A = 1/2(8) A = 4 cm 

Beräkna volymen av en pyramid
För att beräkna volymen av en pyramid, multiplicera arean av basen med höjden på pyramiden. Dela resultatet med 3, det är allt! Läs den här artikeln med beräkningsmetoder för en pyramid med en rektangulär bas och en pyramid med en triangulär bas.
Steg
Metod 1 av 2: Pyramid med rektangulär bas

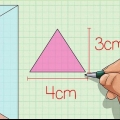
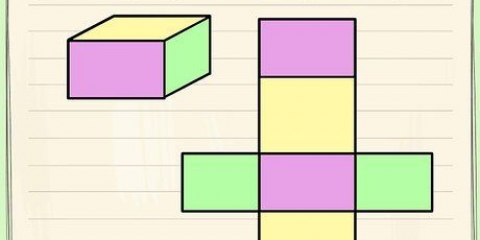
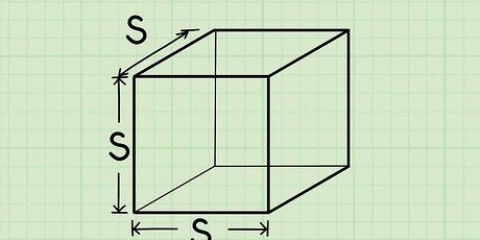
1. Bestäm basens längd och bredd. I det här exemplet är längden 4 cm och bredden 3 cm. Om du har en kvadratisk bas är metoden densamma, bara längden och bredden är lika. Skriv ner dina mått.

2. Multiplicera längden med bredden för att beräkna basens yta. För att beräkna arean av vårt exempel multiplicerar vi 3 cm med 4 cm. 3cm x 4cm = 12cm

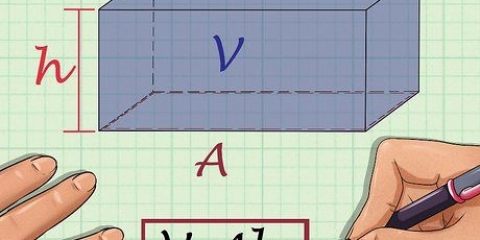
3. Multiplicera arean av basen med höjden. Arean av basen är 12 cm och höjden är 4 cm, så vi multiplicerar 12 cm med 4 cm. 12cm x 4cm = 48cm

4. Dela resultatet med 3. Det är samma sak som att multiplicera med 1/3. 48cm/3 = 16cm. Volymen av en pyramid med en höjd av 4 cm och en rektangulär bas med en bredd på 3 cm och en längd av 4 cm är därför 16 cm. Glöm inte att ange utfallet i kubikenheter.
Metod 2 av 2: Pyramid med en triangulär bas

1. Bestäm basens längd och bredd. Basens längd och bredd måste vinkelrätt mot varandra, annars kommer den här metoden inte att fungera. De kan också ses som botten och höjden på triangeln. I det här exemplet är triangelns bredd 2 cm och längden 4 cm. Skriv ner det här.

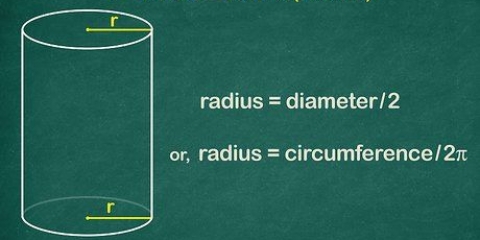
2. Beräkna arean av basen. För att beräkna arean av basen använder vi följande formel:A = 1/2(o)(h). Det är såhär vi gör det:

3. Multiplicera arean av basen med höjden på pyramiden. Arean av basen är 4 cm och höjden är 5 cm. 4cm x 5cm = 20cm.

4. Dela resultatet med 3. 20cm/3 = 6,67cm. Volymen av en pyramid med en höjd av 5 cm och en triangulär bas med en bredd av 2 cm och en längd av 4 cm är därför 6,67 cm.
Tips
- I en pyramid med kvadratisk bas är höjden, linjen som delar den triangulära sidan i två lika trianglar och basens bredd sammankopplade med Pythagoras sats: (bredd ÷ 2) + (höjd) = (triangelns höjd)
- Denna metod kan också tillämpas på föremål som femkantiga pyramider, sexkantiga pyramider, etc. Den allmänna processen är: A) beräkna arean av basen; B) mät höjden från toppen av pyramiden till mitten av basen; C) multiplicera A med B; D) dividera med 3.
- I alla vanlig pyramider är de upprättstående revbenen, linjen som delar den triangulära sidan i två lika trianglar och bredden på basen som är förenad med Pythagoras sats: (sidans längd ÷ 2) + (längden på revbenet) = (höjd)
Varningar
- Pyramider har tre typer av höjder: linjen som delar den triangulära ytan i två lika trianglar, längden på revbenet (längs sidan av en triangulär yta) och den faktiska höjden (från pyramidens spets vinkelrätt ner till basen) . ).
"Beräkna volymen av en pyramid"
Оцените, пожалуйста статью