Hur man beräknar arean av en fyrhörning

Steg

Så för dina läxor måste du beräkna arean av en fyrhörning...men du har inte ens en aning om vad en fyrhörning är. Få inte panik – räddningen är nära! En fyrhörning är vilken figur som helst som består av 4 sidor/vinklar. Allt du behöver göra är att bestämma den fyrsidiga typen av problemet och använda motsvarande formel för att beräkna arean.

Steg

Metod 1 av 4: Kvadrater, rektanglar och andra parallellogram

1. Lär dig hur du avgör vad ett parallellogram är. Ett parallellogram är vilken fyrhörning som helst med 2 par parallella sidor, där de parallella sidorna är lika långa. Kvadrater, rektanglar och romber är alla parallellogram.

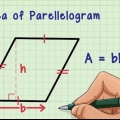
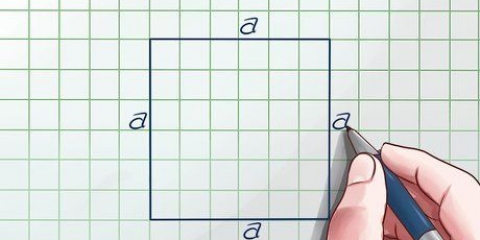
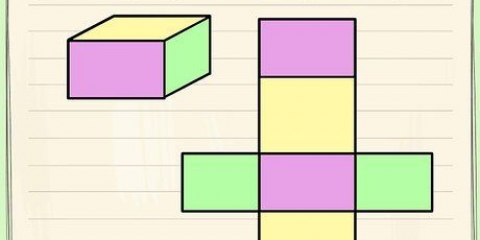
2. Hitta arean av en kvadrat. Eftersom varje sida av en kvadrat är lika lång behöver du bara mäta längden på en sida (kalla det "t"), för att hitta arean av en kvadrat. Detta är samma sak som att multiplicera kvadratens bas med dess höjd; basen och höjden är alltid desamma. Använd följande formel:

K = t

Detta är samma sak som K = t * t

Om en sida av en kvadrat har längden 4, (t = 4), är arean t, eller 4 x 4 = 16.

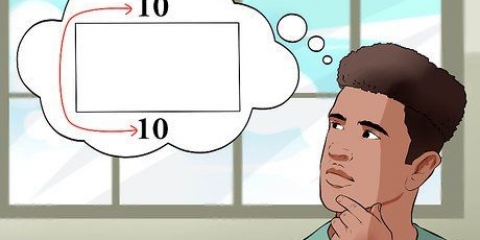
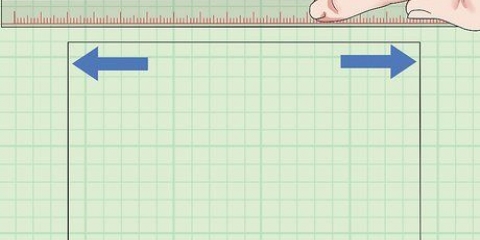
3. Hitta arean av en rektangel. För att hitta arean av en rektangel är det nödvändigt att känna till rektangelns längd och bredd. Formeln är följande:

K = b*h

Om längden är längd 10 och bredden är 5, är rektangelns yta 10 x 5 (l * w) = 50.

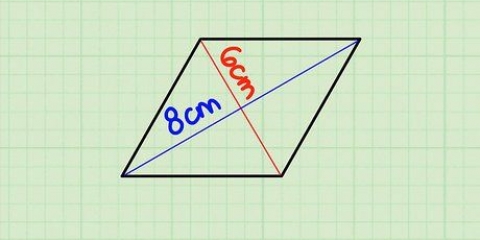
4. Hitta arean av en kvadrat. Det här kan vara knepigt - du kan inte bara multiplicera den ena sidan med den andra här. Du måste nu rita linjer från varje punkt och mäta diagonalerna på formen, om den inte anges. Multiplicera sedan diagonalerna så här:

K = (b*h)/2, där b = diagonal 1 och h = diagonal 2

Om en kvadrat har diagonaler med längden 6 sedan 8, är arean (6 x 8)/2 = 48/2 = 24

Metod 2 av 4: Arean av en trapets

1. Bestäm om det är en trapets. En trapets är en fyrhörning med minst 2 sidor som är parallella. Var och en av de fyra sidorna av en trapets kan ha olika längd. Det finns två olika sätt att hitta arean av en trapets, beroende på den information som ges.

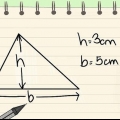
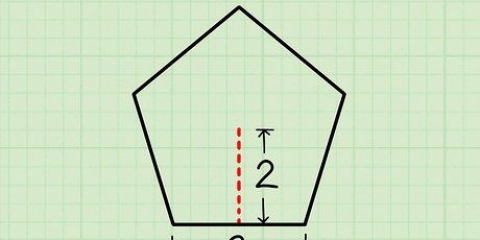
2. Bestäm trapetsens höjd. Höjden på en trapets är den vinkelräta linjen som förbinder den övre baslinjen och den nedre baslinjen, och du behöver båda för att beräkna arean. Detta är inte av samma längd som en av sidorna, eftersom varje sida är diagonal. Så här hittar du höjden:

Bestäm vad den kortaste basen är. Placera din penna i hörnet mellan baslinjen och rita en linje rakt upp eller ner till den andra baslinjen. Du ska nu ha ritat en triangel med en vinkel på 90 grader.

Använd trigonometri för att bestämma höjden. Till exempel, om du vet längden på en sida och den intilliggande vinkeln är känd, och det finns en 90 graders vinkel i triangeln, så är höjden längden på sidan gånger vinkelns sinus.

Antag att höjden på trapetsen är 10.

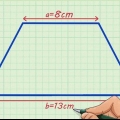
3. Bestäm arean av trapetsen med höjden och längden på basen. Om du vet höjden på trapetsen och längden på båda bassidorna, använd följande formel:

K = (a+b)/2 * h

Om höjden är 10 och basen har en längd av 7 och 9, kan du hitta arean genom att beräkna: (7 + 9)/2 * 10 = (16/2) * 10 = 8 * 10 = 80

4. Hitta arean för en trapets med mittsegmentet. Detta mittsegment är en linje som löper parallellt med trapetsens nedre och övre linje, och har en längd exakt däremellan. Så här jobbar du:

Bestäm mittsegmentet. För att bestämma längden på mittsegmentet m, vi tar medelvärdet av sidornas längder a och b (eller trapetsens nedre och övre linje).Använd formeln: m = (a+b)/2.Nu när du vet längden på mittsegmentet kan du multiplicera det med höjden för att hitta arean. Använd följande formel:

K = m*h

Detta är i huvudsak samma formel som originalet, men ersätter nu "m" termen (a + b)/2.

Anta att du känner till mittsegmentet av denna trapets. Antag att detta är 8, då är trapetsens area 8 x 10 = 80, precis som med föregående metod.

Metod 3 av 4: Bestämma ytan på en drake

1. Vad är en drake. En drake definieras som en geometrisk form där 2 par lika långa sidor är sammankopplade, vilket liknar en vanlig drake. Det finns två olika sätt att hitta arean av denna figur, beroende på den information som ges.

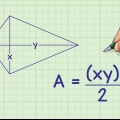
2. Hitta arean på en drake med hjälp av längden på dess sidor. Om du vet längden på två olika sidor av en drake och du vet vinkeln mellan dessa sidor, använd följande formel där vinkeln är lika med theta (θ):

K =(a*b) * sin θ

3. Hitta arean på en drake med hjälp av diagonalerna. En diagonal är den raka linjen mellan två motsatta hörn av draken. Varje drake har 2 diagonaler.

Bestäm längden på varje diagonal. Rita en linje från ena hörnet av en drake till det motsatta. Du bör nu ha 2 trianglar. Bestäm att använda Denna artikel, vad är längden på diagonalen (de tre vinklarna i en triangel blir 180 grader).

När du har bestämt den första diagonalen, använd samma principer för att bestämma längden på den andra. Använd sedan denna formel för att bestämma området, var sid och q representerar längden på diagonalerna:

K = (p*q)/2

Om diagonalerna har längderna 4 och 6, kan du hitta drakens yta enligt följande: (4 x 6)/2 = 24/2 = 12

Observera att denna formel också fungerar för arean av en romb, eftersom detta är en speciell typ av drake, där alla sidor är lika långa.

Metod 4 av 4: En allmän formel

1. Den allmänna formeln för att bestämma arean av en fyrhörning. Det finns formler för att bestämma arean för vilken fyrhörning som helst, oavsett dess form. Här är den mest allmänna formen, med hjälp av trigonometriska principer:

om k är fyrhörningens totala yta, a, b, c och d representerar längden på de fyra sidorna, a är vinkeln (i grader) mellan sidorna a och d och C är vinkeln (i grader) mellan sidorna b och c, sedan:
K = 0.5*a*d * sin A + 0.5*b*c * sin C
Om du försöker hitta arean av ett parallellogram där de motsatta vinklarna är lika, blir formeln enklare: K = 0.5*(ad + bc) * sin A.