Yta = 1/2 x (3 cm x 5 cm) 
Yta = 1/2 x (3 cm x 5 cm) Yta = 1/2 x 15 cm Area = 7.5 cm 

Area = √{6 (6 - 3)(6 - 4)(6 - 5)} 
6 - 3 = 3 6 - 4 = 2 6 - 5 = 1 Area = √{6 (3)(2)(1)} 









Area = 1/2(b)(c) x sin A Area = 1/2(150)(231) x sin A 
Area = 1/2(150)(231) x sin A Area = 1/2(34 650) x sin A Area = 17.325 x sin A Yta = 17 325 x .8386705 Yta = 14.530 cm
Beräkna arean av en triangel
Även om den vanligaste metoden för att beräkna arean av en triangel är att multiplicera dess halva bas med dess höjd, finns det ett antal andra sätt att beräkna arean av en triangel, beroende på tillgängliga data. Detta inkluderar längden på alla tre sidor, längden på en sida av en liksidig triangel och längden på två sidor tillsammans med den inkluderade vinkeln. Läs här hur du kan beräkna arean av en triangel med hjälp av dessa data.
Steg
Metod 1 av 4: Med basen och höjden

1. Bestäm basen och höjden på din triangel. Basen av triangeln är längden på en sida, som vanligtvis är den nedre sidan av triangeln. Höjd är längden från basen till det övre hörnet av triangeln, som är vinkelrät mot basen. I en rätvinklig triangel är basen och höjden de två sidorna som möts i en 90-graders vinkel. Men i en annan triangel, som ses nedan, kommer höjdlinjen att skära rakt igenom formen.
- När du har bestämt basen och höjden på triangeln är du redo att börja använda formeln.

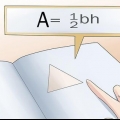
2. Skriv ner formeln för att hitta arean av en triangel. Formeln för denna typ av problem är Area = 1/2 (bas x höjd), eller 1/2 (bh). När du har noterat allt kan du börja fylla i längden på höjden och basen.

3. Ange bas- och höjdvärden. Hitta basen och höjden på triangeln och använd dessa värden i ekvationen. I det här exemplet är triangelns höjd 3 cm och basen på triangeln 5 cm. Så här skulle formeln se ut efter att ha angett dessa värden:

4. Lös ekvationen. Du kan multiplicera höjden gånger basen först eftersom dessa värden står inom parentes. Sedan multiplicerar du resultatet med 1/2. Kom ihåg att du kommer att ge svaret i kvadratmeter eftersom du arbetar i tvådimensionellt rum. Så här löser du detta för det slutliga svaret:
Metod 2 av 4: Använd längden på varje sida (Heron`s Formula)

1. Beräkna halvomkretsen (semiperimeter) av triangeln. För att hitta triangelns halva omkrets behöver du bara lägga ihop alla sidorna och dividera resultatet med två. Formeln för att hitta halva omkretsen av en triangel är följande: semiperimeter = (längden på sidan a + längden på sidan b + längden på sidan c) / 2, eller s = (a + b + c) / 2. Eftersom alla tre längderna av den räta triangeln är givna, 3 cm, 4 cm och 5 cm, kan du koppla in dessa direkt i formlerna och lösa problemet för den halva omkretsen:
- s = (3 + 4 + 5)/2
- s = 12/2
- s = 6

2. Ange de korrekta värdena i formeln för att hitta arean av en triangel. Denna formel för att hitta arean av en triangel kallas även Herons formel och går så här: Area = √{s (s - a)(s - b)(s - c)}. Vi upprepar föregående steg där s halva omkretsen är och a, b, och c triangelns tre sidor. Använd följande operationssekvens: börja med att lösa allt inom parentesen, sedan allt under det radikala tecknet och slutligen själva kvadratroten. Så här kommer formeln att se ut när du har angett alla kända värden:

3. Subtrahera värdena inom parentesen. Alltså: 6 - 3, 6 - 4 och 6 - 5. Här är resultatet på papper:

4. Multiplicera resultaten av dessa operationer. Multiplicera 3 x 2 x 1 för att få 6 som svar. Du måste multiplicera dessa tal tillsammans innan du multiplicerar dem med 6 eftersom de står inom parentes.

5. Multiplicera det föregående resultatet med halva omkretsen. Multiplicera sedan resultatet, 6, med halva omkretsen, som också är 6. 6 x 6 = 36.

6. Beräkna kvadratroten. 36 är en perfekt kvadrat och √36 = 6. Glöm inte enheten du började med -- centimeter. Uttryck det slutliga svaret i kvadratcentimeter. Arean av triangeln med sidorna 3, 4 och 5 är 6 cm.
Metod 3 av 4: Använd en sida av en rektangulär triangel

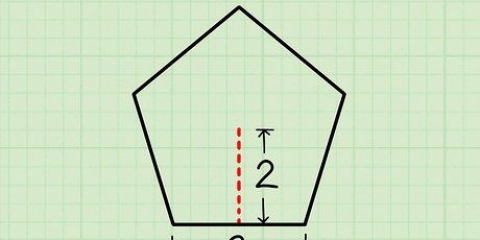
1. Hitta sidan på den liksidiga triangeln. En liksidig triangel har lika långa sidor och lika stora vinklar. Du vet att du har att göra med en liksidig triangel, antingen för att den är given eller för att du vet att alla vinklar och alla sidor har samma värde. Värdet på en av sidorna i denna triangel är 6 cm. Notera detta.
- Om du vet att du har att göra med en liksidig triangel men bara omkretsen är känd, dividera bara detta värde med 3. Till exempel är längden på en sida av en liksidig triangel med omkrets 9 mycket enkelt 9/3, eller 3.

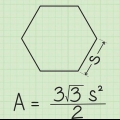
2. Skriv ner formeln för att hitta arean av en liksidig triangel. Formeln för denna typ av problem är area = (s^2)(√3)/4. Anteckna det s "silke" betyder.

3. Tillämpa värdet av en sida på ekvationen. Beräkna först kvadraten på sidan med värdet 6 för att få 36. Hitta sedan värdet på √3, om svaret ska anges med decimaler. Ange nu √3 i din kalkylator för att få 1.732 att få. Dividera detta nummer med 4. Observera att du också kan dividera 36 med 4 och sedan multiplicera med √3 -- operationsordningen har ingen effekt på svaret.

4. Lösa. Nu handlar det främst om att bara räkna. 36 x √3/4 = 36 x .433 = 15.59 cm Arean av en liksidig triangel med en sida på 6 cm lång är 15.59 cm.
Metod 4 av 4: Använd längden på två sidor och den inkluderade vinkeln

1. Hitta värdet på längderna på två sidor och den inkluderade vinkeln. Den inkluderade vinkeln är vinkeln mellan de två kända sidorna av triangeln. Du måste känna till dessa värden för att hitta arean av en triangel med den här metoden. Låt oss anta en triangel med följande dimensioner:
- vinkel A = 123º
- sida b = 150 cm
- sida c = 231 cm

2. Skriv ner formeln för att hitta arean av triangeln. Formeln för att hitta arean av en triangel med två kända sidor och en känd inkluderad vinkel är som följer: Area = 1/2(b)(c) x sin A. I denna ekvation representera "b" och "c" längderna på sidorna och "a" hörnet. Du ska alltid ta vinkelns sinus i denna ekvation.

3. Fyll i värdena i ekvationen. Så här ser ekvationen ut när du anger dessa värden:

4. Lösa. För att lösa denna ekvation, multiplicera först sidorna och dividera resultatet med två. Multiplicera sedan detta resultat med vinkelns sinus. Värdet på sinus kan hittas med din miniräknare. Glöm inte att ge ditt svar i kubikenheter. Så här gör du det:
Tips
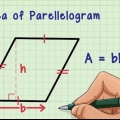
- Om du inte förstår varför den grundläggande - höjdformeln fungerar på detta sätt, kommer här en kort förklaring. Om du gör en andra, identisk triangel och lägger den bredvid varandra, bildar den antingen en rektangel (två räta trianglar) eller ett parallellogram (två icke-räta trianglar). För att hitta arean av en rektangel eller parallellogram behöver du bara multiplicera basen med höjden. Eftersom en triangel är lika med en halv rektangel eller parallellogram, följer det att arean av en triangel är lika med en halv bas gånger dess höjd.
"Beräkna arean av en triangel"
Оцените, пожалуйста статью