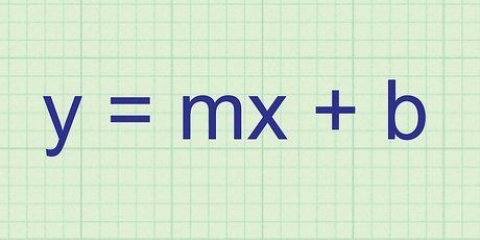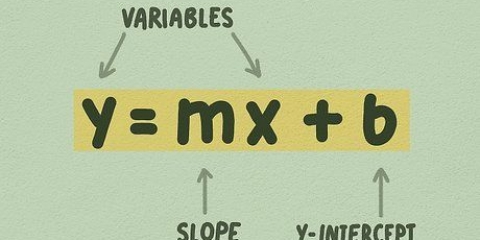Funktioner skrivs ofta som  Detta innebär att funktionen
Detta innebär att funktionen  lägg alltid till 3 till numret du har för
lägg alltid till 3 till numret du har för  Fyll i. Skriver du in 2 skriver du ner
Fyll i. Skriver du in 2 skriver du ner  eller
eller 
Funktioner kan också visa komplexa rörelser. NASA har till exempel en funktion för att beskriva hastigheten på en raket, baserat på bränsleförbrukningshastighet, vindmotstånd och raketens vikt. 

Gränser är lättast att visualisera på en graf – till exempel finns det punkter som är nära att röra en graf, men aldrig riktigt? Gränser kan vara antal, oändliga eller till och med obefintliga. Till exempel med additionssekvensen 1 + 2 + 2 + 2 + 2 + ... och detta fortsätter i det oändliga, sedan blir det slutliga talet oändligt stort. Gränsen blir då oändlig. 
Algebra. Du måste förstå de olika processerna och kunna lösa ekvationer och ekvationssystem med flera variabler. Förstå grunderna i samlingar. Träna på att göra grafer. Geometri. Geometri är studiet av former. Du bör ha grundläggande kunskaper om trianglar, rektanglar och cirklar, och hur man räknar ut saker som omkrets och area. Förstå vinklar, linjer och koordinater trigonometri. Trigonometri är den gren av matematik som handlar om egenskaperna hos cirklar och räta trianglar. Kunna använda trigonometriska identiteter, grafer, funktioner och inversa trigonometriska funktioner. 
Många smartphones och surfplattor erbjuder idag billiga men effektiva grafappar om du inte vill eller inte kan köpa en grafräknare. 

Acceleration är en derivata – den berättar hur snabbt något accelererar eller bromsar, dvs hur dess hastighet ändras. 
Linjens lutning är förändringen i y dividerat med förändringen i x`.` Ju större lutning lutningen är, desto brantare linjen. Så att byta branta linjer innebär ett snabbt byte. Uppdatera dina kunskaper om att bestämma lutningen på en linje om den har sjunkit en bit. 
Till exempel i  du kan välja vilka två punkter som helst och beräkna lutningen. ta
du kan välja vilka två punkter som helst och beräkna lutningen. ta  och
och  Lutningen mellan dessa punkter är då lika med
Lutningen mellan dessa punkter är då lika med  Detta innebär att bytet mellan
Detta innebär att bytet mellan  och
och  är lika med 2.
är lika med 2. 
Till exempel undersöker forskare hur snabbt vissa arter dör ut för att rädda dem. Men fler djur dör på vintern än på sommaren, så det är inte användbart att studera förändringstakten över hela året - det är bättre att bestämma förändringstakten inom en mindre period, som från 1 juli till 1 augusti. 
Tänk på exemplet där du fortsätter att dividera 1 med 2, och med det 1/2, 1/4, 1/8 osv. får. Så i slutändan kommer du nära noll, och svaret är "nästan noll". Punkterna är så nära varandra att de är "nästan lika". Detta är karaktären hos derivat. 

Det finns olika notationer för derivator. I det föregående steget indikerades derivat med en indikator --- derivatan av  skriv sedan ner det som
skriv sedan ner det som  Detta kallas Lagranges notation.
Detta kallas Lagranges notation. Det finns ett annat sätt som ofta används för att skriva derivator. Istället för med omsorg, noterar du  Kom ihåg att funktionen
Kom ihåg att funktionen  beror på variabeln
beror på variabeln  Så vi skriver derivatan som
Så vi skriver derivatan som  --- derivatan av
--- derivatan av  fram tills
fram tills Detta kallas Leibniz .s notation.
Detta kallas Leibniz .s notation. 
Hur snabbt rör sig kulan?? Med vilken hastighet ändras positionen (eller derivatan) av den rörliga kulan?? Vi kallar denna derivata `hastighet`. Rulla kulan nerför en ramp och se hur hastigheten förändras. Vilken är förändringshastigheten, eller derivatan, av kulans hastighet?? Denna derivata är vad vi kallar "acceleration". Rulla marmorn längs en böljande bana, som en berg-och dalbana. Hur mycket tar kulan fart när den rullar ner, och hur mycket saktar kulan uppför?? Hur fort går kulan exakt när den är halvvägs uppför första backen? Detta är då den momentana förändringshastigheten, eller derivatan, av den marmorn vid den specifika punkten. 




Anta att du lägger ihop många små segment under grafen, och att bredden på varje segment nästan noll är. 
Den första symbolen,  är symbolen för integration (detta är faktiskt ett sträckt S).
är symbolen för integration (detta är faktiskt ett sträckt S). Den andra delen,  är funktionen. Om det är inuti integralen kallas det de väsentlig.
är funktionen. Om det är inuti integralen kallas det de väsentlig. Och slutligen  i slutet, som talar om vilken variabel du integrerar och till vilken. Eftersom funktionen
i slutet, som talar om vilken variabel du integrerar och till vilken. Eftersom funktionen  beroende på
beroende på  är det som man integrerar mot.
är det som man integrerar mot. Kom ihåg att variabeln du integrerar kanske inte alltid är det  kommer att vara, så var försiktig med vad du skriver ner.
kommer att vara, så var försiktig med vad du skriver ner. 
Integrera genom substitution. Beräknar obestämda integraler. Integrera genom att dela. 
Kom till exempel ihåg att derivatan av hastighet är acceleration, så du kan använda hastighet för att hitta acceleration. Men om du bara känner till accelerationen av något (som föremål som faller på grund av gravitationen), kan du integrera för att hitta hastigheten igen! 
Detta låter dig bestämma volymen av ett fast ämne, så länge du har en funktion som representerar det. Du kan till exempel skapa en funktion som följer botten av en sjö och sedan använda den för att bestämma sjöns volym, eller hur mycket vatten den innehåller.
Förstå analys
Analys (även kallad kalkyl) är en gren av matematiken fokuserad på gränser, funktioner, derivator, integraler och oändliga serier. Detta ämne täcker mycket av matematik och ligger till grund för många av de formler och ekvationer som används inom fysik och mekanik. Du kommer förmodligen att behöva flera år av matematik på gymnasiet för att förstå analysen ordentligt, men den här artikeln kommer att hjälpa dig att känna igen nyckelbegreppen, samt en bättre förståelse av teorin.
Steg
Del 1 av 3: Analysens grunder

1. Analys är studiet av hur saker förändras. Analys är en gren av matematiken som undersöker siffror och grafer, vanligtvis hämtade från verkliga data, och förklarar hur de förändras. Även om detta kanske inte verkar särskilt användbart till en början, är analys en av de mest använda grenarna av matematik. Föreställ dig att ha verktygen som kan berätta hur snabbt ditt företag växer vid varje given tidpunkt, eller för att kartlägga kursen för ett rymdskepp och hur snabbt bränslet förbrukas. Analys är ett viktigt verktyg inom teknik, ekonomi, statistik, kemi och fysik och har bidragit till många uppfinningar och upptäckter.

2. Funktioner är relationer mellan två tal och används för att kartlägga relationer. De är regler för förhållandet mellan tal, och matematiker använder dem för att göra grafer. I en funktion har varje ingång exakt ett resultat. Till exempel: in  returnerar valfritt värde på
returnerar valfritt värde på  ett nytt värde för
ett nytt värde för  I händelse av att
I händelse av att  då är
då är  I händelse av att
I händelse av att  , sedan
, sedan  Analys studerar alltid funktioner och hur de förändras, och använder dessa funktioner för att kartlägga samband.
Analys studerar alltid funktioner och hur de förändras, och använder dessa funktioner för att kartlägga samband.
 returnerar valfritt värde på
returnerar valfritt värde på  ett nytt värde för
ett nytt värde för  I händelse av att
I händelse av att  då är
då är  I händelse av att
I händelse av att  , sedan
, sedan  Analys studerar alltid funktioner och hur de förändras, och använder dessa funktioner för att kartlägga samband.
Analys studerar alltid funktioner och hur de förändras, och använder dessa funktioner för att kartlägga samband. Detta innebär att funktionen
Detta innebär att funktionen  lägg alltid till 3 till numret du har för
lägg alltid till 3 till numret du har för  Fyll i. Skriver du in 2 skriver du ner
Fyll i. Skriver du in 2 skriver du ner  eller
eller 

3. Tänk på begreppet oändlighet. Oändlighet är den kontinuerliga upprepningen av en process. Det är inte en specifik plats (du kan inte gå till oändligheten), utan snarare beteendet hos ett tal eller en ekvation, om det görs för alltid. Detta är viktigt för att studera förändring: du kanske vill veta hur snabbt din bil rör sig vid ett givet ögonblick, men är det hur snabbt din bil rör sig under den aktuella sekunden?? millisekund? Nanosekund? Du kan hitta oändligt mycket mindre bitar av tid för att vara ännu mer exakt, och det är då analysen börjar.

4. Förstå begreppet gränser. En gräns talar om vad som händer när något närmar sig oändligheten. Ta talet 1 och dividera det med 2. Fortsätt att dividera med 2, om och om igen. 1 blir ½ och sedan 1/4, 1/8, 1/16, 1/32 osv. Varje gång siffran blir mindre och mindre, "närmare" noll. Men var tar det stopp? Hur många gånger måste du dividera 1 med 2 för att få noll?? Istället för att svara på denna fråga föreslår du i analysen ett begränsa I det här fallet är gränsen.

5. Gå igenom de väsentliga matematiska begreppen algebra, trigonometri och grunderna i matematik. Analys bygger på mycket av den matematik du har lärt dig tidigare. Att vara väl insatt i alla ämnen gör det mycket lättare att lära sig och förstå analys. Några ämnen att fräscha upp dina kunskaper om är:

6. Skaffa en grafräknare. Analys är inte lätt att förstå utan att se vad du gör. Grafräknare gör funktioner visuella så att du bättre kan förstå vilka ekvationer du har att göra med. Ofta visas även gränserna på skärmen, och derivatan och funktionerna beräknas automatiskt.
Del 2 av 3: Förstå derivator

1. Analys används för att studera "förändring i ett specifikt ögonblick". Att veta varför något förändras i ett exakt ögonblick är kärnan i analysen. Till exempel, analys ger dig inte bara hastigheten på en bil, utan också hur mycket den hastigheten ändras vid ett givet ögonblick. Detta är en av de enklaste användningsområdena för analys, men mycket viktigt. Föreställ dig hur viktig sådan information är för att bestämma hastigheten som behövs för att få ett rymdskepp till månen!
- Att bestämma förändring vid ett givet ögonblick har skilja. Differentiering är den första av de två stora analysgrenarna.

2. Använd derivator för att förstå hur saker förändras vid ett givet ögonblick. En "derivata" är ett fint ord för något som ofta gör eleverna nervösa. Konceptet i sig är dock inte så svårt att förstå - det betyder bara "hur snabbt något förändras". De derivator som du kommer att stöta på mest i det dagliga livet har med hastighet att göra. Men du brukar inte kalla det för `hastighetens derivata`, utan bara `acceleration`.

3. Vet att förändringshastigheten är lika med lutningen mellan två punkter. Detta är en av analysens viktigaste upptäckter. Förändringshastigheten mellan två punkter är lika med lutningen på linjen mellan dessa två punkter. Tänk bara på en enkel linje, som den i ekvationen  Linjens lutning är 3, vilket betyder att för varje nytt värde på
Linjens lutning är 3, vilket betyder att för varje nytt värde på 
 ändras med 3. Lutningen är densamma som förändringshastigheten: en lutning på tre betyder att linjen ändras med 3 (blir tre gånger större) för varje förändring i
ändras med 3. Lutningen är densamma som förändringshastigheten: en lutning på tre betyder att linjen ändras med 3 (blir tre gånger större) för varje förändring i  När
När  när
när 
 Linjens lutning är 3, vilket betyder att för varje nytt värde på
Linjens lutning är 3, vilket betyder att för varje nytt värde på 
 ändras med 3. Lutningen är densamma som förändringshastigheten: en lutning på tre betyder att linjen ändras med 3 (blir tre gånger större) för varje förändring i
ändras med 3. Lutningen är densamma som förändringshastigheten: en lutning på tre betyder att linjen ändras med 3 (blir tre gånger större) för varje förändring i  När
När  när
när 

4. Vet att du kan bestämma lutningen på krökta linjer. Att bestämma lutningen på en rak linje är relativt enkelt: hur mycket förändras  för något värde av
för något värde av  Men komplexa ekvationer som
Men komplexa ekvationer som  för en kurva är mycket svårare att bestämma. Men du kan fortfarande bestämma förändringshastigheten mellan två punkter -- dra bara en linje mellan de två punkterna och beräkna lutningen.
för en kurva är mycket svårare att bestämma. Men du kan fortfarande bestämma förändringshastigheten mellan två punkter -- dra bara en linje mellan de två punkterna och beräkna lutningen.
 för något värde av
för något värde av  Men komplexa ekvationer som
Men komplexa ekvationer som  för en kurva är mycket svårare att bestämma. Men du kan fortfarande bestämma förändringshastigheten mellan två punkter -- dra bara en linje mellan de två punkterna och beräkna lutningen.
för en kurva är mycket svårare att bestämma. Men du kan fortfarande bestämma förändringshastigheten mellan två punkter -- dra bara en linje mellan de två punkterna och beräkna lutningen. du kan välja vilka två punkter som helst och beräkna lutningen. ta
du kan välja vilka två punkter som helst och beräkna lutningen. ta  och
och  Lutningen mellan dessa punkter är då lika med
Lutningen mellan dessa punkter är då lika med  Detta innebär att bytet mellan
Detta innebär att bytet mellan  och
och  är lika med 2.
är lika med 2.
5. Om du vill beräkna förändringen mer exakt, se till att punkterna ligger närmare varandra. Ju närmare du väljer de två punkterna, desto mer exakt blir ditt svar. Anta att du vill veta hur mycket din bil accelererar när du trycker på gaspedalen. Du vill inte mäta hastighetsförändringen mellan ditt hem och snabbköpet, utan hastighetsförändringen från det ögonblick du trampar på gaspedalen. Ju närmare din avläsning kommer den bråkdelen av en sekund, desto mer exakt blir din beräkning av förändringen.

6. Använd oändligt korta linjer för att bestämma den `momentana förändringshastigheten`, eller hitta derivatan. Det är här analysen ofta blir lite förvirrande, men detta är faktiskt resultatet av två enkla fakta. Först och främst vet du att lutningen på en linje är lika med hur snabbt den linjen ändras. För det andra vet du att ju närmare punkterna på linjen är varandra, desto mer exakt blir avläsningen. Men hur hittar man förändringshastigheten vid en given punkt om lutningen är förhållandet mellan två punkter? Svaret: Du väljer två punkter som ligger oändligt nära varandra.

7. Lär dig hur du bestämmer olika derivator. Det finns många olika tekniker för att hitta en derivata beroende på ekvationen, men de flesta av dem är vettiga när du kommer ihåg grunderna för derivator ovan. Alla derivator är ett sätt att hitta lutningen på en "oändligt liten" linje. Nu när du vet mer om derivatteori är mycket av arbetet att hitta svaren.

8. Bestäm derivatekvationerna för att förutsäga förändringshastigheten när som helst. Det är användbart att bestämma förändringshastigheten vid varje givet tillfälle med hjälp av derivator, men det fina med analys är att du kan skapa en ny modell för vilken funktion som helst. Derivatet av  till exempel är
till exempel är  Det betyder att du kan hitta derivatan för vilken punkt som helst på en graf
Det betyder att du kan hitta derivatan för vilken punkt som helst på en graf  genom att substituera i derivatan. På saken
genom att substituera i derivatan. På saken  varigenom
varigenom  är derivatan 4, eftersom
är derivatan 4, eftersom 
 till exempel är
till exempel är  Det betyder att du kan hitta derivatan för vilken punkt som helst på en graf
Det betyder att du kan hitta derivatan för vilken punkt som helst på en graf  genom att substituera i derivatan. På saken
genom att substituera i derivatan. På saken  varigenom
varigenom  är derivatan 4, eftersom
är derivatan 4, eftersom 
 skriv sedan ner det som
skriv sedan ner det som  Detta kallas Lagranges notation.
Detta kallas Lagranges notation. Kom ihåg att funktionen
Kom ihåg att funktionen  beror på variabeln
beror på variabeln  Så vi skriver derivatan som
Så vi skriver derivatan som  --- derivatan av
--- derivatan av  fram tills
fram tills Detta kallas Leibniz .s notation.
Detta kallas Leibniz .s notation.
9. Försök komma ihåg praktiska exempel på derivat, om du tycker att detta är svårt att förstå. Det enklaste exemplet är baserat på hastighet, och omfattar många olika derivator som vi stöter på varje dag. Glöm inte: en derivata är ett mått på hur snabbt något förändras. Tänk på ett enkelt experiment. Du rullar en kula på ett bord och mäter hur långt den rör sig varje gång och hur snabbt. Föreställ dig nu att den rullande kulan följer en linje på en graf - du använder derivator för att mäta de momentana förändringarna när som helst på den linjen.
Del 3 av 3: Förstå integraler

1. Vet att du kan använda analys för att hitta komplexa områden och volymer. Analys låter dig mäta komplexa former som annars är svåra att mäta. Tänk till exempel på frågan om att vilja veta hur mycket vatten det finns i en lång, oregelbundet formad sjö - det är omöjligt att mäta varje liter vatten individuellt eller att använda en linjal för att mäta sjöns form. Med analys kan du studera hur kanterna på sjön förändras och sedan använda den informationen för att ta reda på hur mycket vatten den innehåller.
- Tillverkningen av geometriska modeller och studiet av volymer har integrera. Integralkalkyl är den andra viktiga analysgrenen.

2. Vet att integration är området under en graf. Integration används för att mäta utrymmet under en linje, vilket gör att du kan bestämma området för konstiga eller oregelbundna former. Ta ekvationen  Det ser ut som ett inverterat "U". Du kan beräkna hur mycket utrymme det finns under U:t med hjälp av integralkalkyl. Du kanske undrar vad poängen med det är, men tänk på dess användning i tillverkningsprocesserna -- du kan skapa en funktion som ser ut som en ny del, och använda integral aritmetik för att hitta arean för den delen, och för att hjälpa dig att beställa rätt mängd material.
Det ser ut som ett inverterat "U". Du kan beräkna hur mycket utrymme det finns under U:t med hjälp av integralkalkyl. Du kanske undrar vad poängen med det är, men tänk på dess användning i tillverkningsprocesserna -- du kan skapa en funktion som ser ut som en ny del, och använda integral aritmetik för att hitta arean för den delen, och för att hjälpa dig att beställa rätt mängd material.
 Det ser ut som ett inverterat "U". Du kan beräkna hur mycket utrymme det finns under U:t med hjälp av integralkalkyl. Du kanske undrar vad poängen med det är, men tänk på dess användning i tillverkningsprocesserna -- du kan skapa en funktion som ser ut som en ny del, och använda integral aritmetik för att hitta arean för den delen, och för att hjälpa dig att beställa rätt mängd material.
Det ser ut som ett inverterat "U". Du kan beräkna hur mycket utrymme det finns under U:t med hjälp av integralkalkyl. Du kanske undrar vad poängen med det är, men tänk på dess användning i tillverkningsprocesserna -- du kan skapa en funktion som ser ut som en ny del, och använda integral aritmetik för att hitta arean för den delen, och för att hjälpa dig att beställa rätt mängd material.
3. Vet att välja ett område att integrera. Du kan inte bara integrera en hel funktion. Till exempel,  är en diagonal linje som fortsätter för evigt, och du kan inte integrera det hela, för det skulle aldrig sluta. När du integrerar funktioner måste du välja ett område, till exempel alla punkter mellan
är en diagonal linje som fortsätter för evigt, och du kan inte integrera det hela, för det skulle aldrig sluta. När du integrerar funktioner måste du välja ett område, till exempel alla punkter mellan och
och 
 är en diagonal linje som fortsätter för evigt, och du kan inte integrera det hela, för det skulle aldrig sluta. När du integrerar funktioner måste du välja ett område, till exempel alla punkter mellan
är en diagonal linje som fortsätter för evigt, och du kan inte integrera det hela, för det skulle aldrig sluta. När du integrerar funktioner måste du välja ett område, till exempel alla punkter mellan och
och 

4. Hur beräknar man arean av en rektangel?. Anta att du har en platt linje ovanför en graf, som t.ex  För att hitta arean under den, hitta arean av en rektangel mellan
För att hitta arean under den, hitta arean av en rektangel mellan  och
och  Detta är lätt att mäta, men det fungerar inte med vågiga linjer eftersom du inte enkelt kan konvertera dem till rektanglar.
Detta är lätt att mäta, men det fungerar inte med vågiga linjer eftersom du inte enkelt kan konvertera dem till rektanglar.
 För att hitta arean under den, hitta arean av en rektangel mellan
För att hitta arean under den, hitta arean av en rektangel mellan  och
och  Detta är lätt att mäta, men det fungerar inte med vågiga linjer eftersom du inte enkelt kan konvertera dem till rektanglar.
Detta är lätt att mäta, men det fungerar inte med vågiga linjer eftersom du inte enkelt kan konvertera dem till rektanglar.
5. Vet att i integralkalkyl läggs många små rektanglar samman för att hitta arean av ett område. Om du förstorar en kurva enormt ser den ut som en rak linje. Du ser detta varje dag -- du kan inte se jordens krökning eftersom du är så nära jordens yta. Integration skapar ett oändligt antal små rektanglar under en kurva som är så små att de i princip är platta, vilket gör att du kan räkna dem. Alla dessa rektanglar adderade tillsammans bildar arean av området under en kurva.

6. Vet hur man läser och skriver integraler korrekt. Integraler består av 4 delar. En typisk integral ser ut så här:


 är symbolen för integration (detta är faktiskt ett sträckt S).
är symbolen för integration (detta är faktiskt ett sträckt S). är funktionen. Om det är inuti integralen kallas det de väsentlig.
är funktionen. Om det är inuti integralen kallas det de väsentlig. i slutet, som talar om vilken variabel du integrerar och till vilken. Eftersom funktionen
i slutet, som talar om vilken variabel du integrerar och till vilken. Eftersom funktionen  beroende på
beroende på  är det som man integrerar mot.
är det som man integrerar mot. kommer att vara, så var försiktig med vad du skriver ner.
kommer att vara, så var försiktig med vad du skriver ner.
7. Läs mer om att hitta integraler. Integralkalkyl finns i många former, och du måste lära dig många olika formler för att integrera varje funktion. Men de följer alla principerna ovan: integration är summan av ett oändligt antal saker.

8. Vet att integration är motsatsen till differentiering och vice versa. Detta är en tumregel för analys som är så viktig att den har fått ett eget namn: Integralkontots grundläggande sats. Eftersom integration och differentiering är så nära besläktade, kan en kombination av de två användas för att mäta förändringshastighet, acceleration, hastighet, plats, rörelse, etc. att avgöra, oavsett vilken information du har.

9. Vet att integration också låter dig kontrollera volymen på 3D-objekt. Att snurra en platt form är ett sätt att skapa 3D solids. Föreställ dig bara att ett mynt på bordet snurrar - lägg märke till hur myntet ser ut att ta formen av en sfär när det snurrar. Detta koncept låter dig bestämma volym genom en process som kallas "volym genom rotation".
Tips
- Övning ger färdighet, så gör övningsövningarna i din lärobok – även de som din lärare inte har angett – och kontrollera dina svar så att du bättre förstår begreppen.
- Om du inte kan komma på något, fråga din lärare.
Оцените, пожалуйста статью