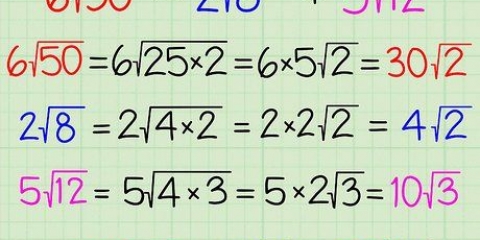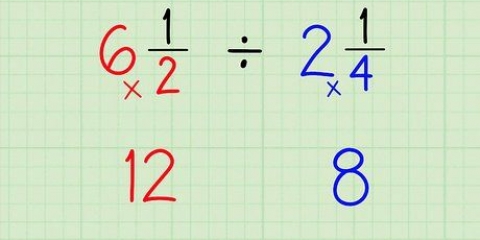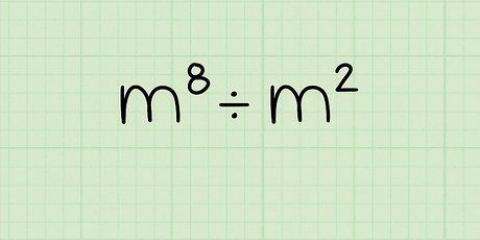Dela kvadratrötter

Steg
Tips
Varningar

Att dividera med kvadratrötter är i huvudsak en förenkling av en bråkdel. Naturligtvis gör närvaron av kvadratrötter processen lite mer komplicerad, men det finns regler som gör att vi kan arbeta med bråk på ett relativt enkelt sätt. Det viktigaste att komma ihåg är att du måste dividera koefficienter med koefficienter och rötter med rötter. Du ska heller aldrig lämna en kvadratrot i en nämnare.

Steg

Metod 1 av 4: Dela morötter

1. Ställ upp fraktionen. Om uttrycket inte redan är i form av ett bråk, skriv om det så här. Detta gör det lättare att följa alla nödvändiga steg för att dividera med en kvadratrot. Kom ihåg att ett divisionstecken är detsamma som ett bråkstapel.

Till exempel om du $\sqrt{144} \div \sqrt{36}$ ${sqrt{144}}div {sqrt{36}}$ beräknar och skriv sedan om problemet som: $\frac{\sqrt{144}}{\sqrt{36}}$ ${frac{{sqrt{144}}}{{sqrt{36}}}}$ .

Bild med titeln Divide Square Roots Steg 2

2. Använd ett radikalt tecken. Om ditt problem har en kvadratrot i täljaren och nämnaren kan du placera båda rötterna under en radikal. (En rot är talet under radikalen.) Detta gör det ännu enklare att förenkla.

Till exempel,

\frac{\sqrt{144}}{\sqrt{36}}

${frac{{sqrt{144}}}{{sqrt{36}}}}$ kan skrivas om som

\sqrt{\frac{144}{36}}

${sqrt{{frac{144}{36}}}}$ .

Bild med titeln Dela kvadratrötter Steg 3

3. Dela rötterna. Dela talen som du skulle göra med vilket heltal som helst. Se till att placera kvoten under en ny radikal.

Till exempel,

\frac{144}{36} = 4

${frac{144}{36}}=4$ , Så

\sqrt{\frac{144}{36}} = \sqrt{4}

${sqrt{{frac{144}{36}}}}={sqrt{4}}$ .

Bild med titeln Dela kvadratrötter Steg 4

4. Förenkla, Om nödvändigt. Om rotnumret är en kvadrat, eller om en av faktorerna är en perfekt kvadrat, måste du förenkla uttrycket. En kvadrat eller perfekt kvadrat är produkten av ett heltal multiplicerat med sig själv. Till exempel är 25 en perfekt kvadrat eftersom

5 \times 5 = 25

$5 gånger 5=25$ .

Till exempel är 4 en perfekt kvadrat eftersom

2 \times 2 = 4

$2 gånger 2=4$ . Således:

\sqrt{4}

${sqrt{4}}$

= \sqrt{2 \times 2}

$={sqrt{2times 2}}$

= 2

$=2$
så,

\frac{\sqrt{144}}{\sqrt{36}} = \sqrt{4} = 2

${frac{{sqrt{144}}}{{sqrt{36}}}}={sqrt{4}}=2$ .

Metod 2 av 4: Factoring roots

Bild med titeln Dela kvadratrötter Steg 5

1. Uttryck problemet som en bråkdel. Uttrycket är förmodligen redan skrivet så här. Om inte, ändra det. Att göra det till en bråkdel gör de nödvändiga stegen lättare att följa, särskilt när du faktorisera kvadratrötter. Kom ihåg att ett divisionstecken är detsamma som ett bråkstapel.

Till exempel vid beräkning $\sqrt{8} \div \sqrt{36}$ ${sqrt{8}}div {sqrt{36}}$ , skriv om uttrycket som: $\frac{\sqrt{8}}{\sqrt{36}}$ ${frac{{sqrt{8}}}{{sqrt{36}}}}$ .

Bild med titeln Dela kvadratrötter Steg 6

2. Faktorera varje morot i faktorer. Faktorisera talet som ett heltal. Lämna faktorerna under de radikala tecknen.

Till exempel:

\frac{\sqrt{8}}{\sqrt{36}} = \frac{\sqrt{2 \times 2 \times 2}}{\sqrt{6 \times 6}}

${frac{{sqrt{8}}}{{sqrt{36}}}}={frac{{sqrt{2 gånger 2 gånger 2}}}{{sqrt{6 gånger 6 }}}}$

Bild med titeln Dela kvadratrötter Steg 7

3. Förenkla bråkets täljare och nämnare. Till för att förenkla en kvadratrot, utesluter du alla faktorer där produkten är en kvadrat?. En kvadrat är resultatet av ett heltal multiplicerat med sig själv. Faktorn blir nu en koefficient utanför kvadratroten.

Till exempel:

\sqrt{} 2 \times 2 \times 2 \sqrt{6 \times 6}

${frac{{sqrt{{cancel{2times 2times }}2}}}{{sqrt{{cancel{6times 6}}}}}}}$

2 \sqrt{2} 6

${frac{2{sqrt{2}}}{6}}$
så,

\frac{\sqrt{8}}{\sqrt{36}} = 2 \sqrt{2} 6

${frac{{sqrt{8}}}{{sqrt{36}}}}={frac{2{sqrt{2}}}{6}}$

Bild med titeln Dela kvadratrötter Steg 8

4. Eliminera det radikala tecknet från nämnaren, om det behövs. Som regel kan ett uttryck inte ha en kvadratrot i nämnaren. Om din bråkdel har en kvadratrot i nämnaren måste du eliminera den. Detta innebär att man tar bort roten i nämnaren. För att göra detta, multiplicera täljaren och nämnaren för bråket med kvadratroten du behöver eliminera.

Anta till exempel att ditt uttryck är det

6 \sqrt{2} \sqrt{3}

${frac{6{sqrt{2}}}{{sqrt{3}}}}$ , då måste du multiplicera täljaren och nämnaren med

\sqrt{3}

${sqrt{3}}$ för att ta bort kvadratroten från nämnaren:

6 \sqrt{2} \sqrt{3} \times \frac{\sqrt{3}}{\sqrt{3}}

${frac{6{sqrt{2}}}{{sqrt{3}}}} gånger {frac{{sqrt{3}}}{{sqrt{3}}}}$

= 6 \sqrt{2} \times \sqrt{3} \sqrt{3} \times \sqrt{3}

$={frac{6{sqrt{2}}times {sqrt{3}}}{{sqrt{3}}times {sqrt{3}}}}$

= 6 \sqrt{6} \sqrt{9}

$={frac{6{sqrt{6}}}{{sqrt{9}}}}$

= 6 \sqrt{6} 3

$={frac{6{sqrt{6}}}{3}}$ .

Bild med titeln Divide Square Roots Steg 9

5. Förenkla ytterligare om det behövs. Ibland står man kvar med koefficienter som kan förenklas ytterligare, eller minska. Förenkla heltal i täljaren och nämnaren precis som du skulle förenkla ett bråk.

Till exempel,

\frac{2}{6}

${frac{2}{6}}$ kan reduceras till

\frac{1}{3}

${frac{1}{3}}$ , Så

2 \sqrt{2} 6

${frac{2{sqrt{2}}}{6}}$ kan reduceras till

1 \sqrt{2} 3

${frac{1{sqrt{2}}}{3}}$ , eller bara

\frac{\sqrt{2}}{3}

${frac{{sqrt{2}}}{3}}$ .

Metod 3 av 4: Dela kvadratrötter med koefficienter

Bild med titeln Divide Square Roots Steg 10

1. Förenkla koefficienterna. Det här är siffrorna utanför radikalen. För att förenkla dem, dela eller minska, ignorera kvadratrötterna för nu.

Till exempel om du $4 \sqrt{32} 6 \sqrt{16}$ ${frac{4{sqrt{32}}}{6{sqrt{16}}}}$ måste räkna, då förenklar du först $\frac{4}{6}$ ${frac{4}{6}}$ . Både täljaren och nämnaren kan delas med en faktor 2. Så du kan förenkla detta till: $\frac{4}{6} = \frac{2}{3}$ ${frac{4}{6}}={frac{2}{3}}$ .

Bild med titeln Divide Square Roots Steg 11

2. Förenkla kvadratrötterna. Om täljaren är delbar med nämnaren, dela bara talen under radikalerna. Om inte, förenkla varje kvadratrot på samma sätt som andra kvadratrötter.

Till exempel, eftersom 32 är delbart med 16, kan du dividera kvadratrötterna:

\sqrt{\frac{32}{16}} = \sqrt{2}

${sqrt{{frac{32}{16}}}}={sqrt{2}}$ .

Bild med titeln Dela kvadratrötter Steg 12

3. Multiplicera de förenklade koefficienterna med den förenklade kvadratroten. Kom ihåg att det inte kan finnas en kvadratrot i en nämnare, så när du multiplicerar ett bråk med en kvadratrot, sätter du kvadratroten i täljaren.

Till exempel,

\frac{2}{3} \times \sqrt{2} = 2 \sqrt{2} 3

${frac{2}{3}}times {sqrt{2}}={frac{2{sqrt{2}}}{3}}$ .

Bild med titeln Divide Square Roots Steg 13

4. Eliminera kvadratroten i nämnaren, om det behövs. Detta kallas rationalisering av nämnaren. Regeln är att ett uttryck inte kan ha en kvadratrot i nämnaren. För att subtrahera roten från nämnaren, multiplicera täljaren och nämnaren med kvadratroten du vill subtrahera.

Till exempel om du har ett uttryck som

4 \sqrt{3} 2 \sqrt{7}

${frac{4{sqrt{3}}}{2{sqrt{7}}}}$ , då måste du multiplicera täljaren och nämnaren med

\sqrt{7}

${sqrt{7}}$ för att eliminera kvadratroten i nämnaren:

4 \sqrt{3} \sqrt{7} \times \frac{\sqrt{7}}{\sqrt{7}}

${frac{4{sqrt{3}}}{{sqrt{7}}}} gånger {frac{{sqrt{7}}}{{sqrt{7}}}}$

= 4 \sqrt{3} \times \sqrt{7} \sqrt{7} \times \sqrt{7}

$={frac{4{sqrt{3}}times {sqrt{7}}}{{sqrt{7}}times {sqrt{7}}}}$

= 4 \sqrt{21} \sqrt{49}

$={frac{4{sqrt{21}}}{{sqrt{49}}}}$

= 4 \sqrt{21} 7

$={frac{4{sqrt{21}}}{7}}$

Metod 4 av 4: Dividera med ett binomial med kvadratrot

Bild med titeln Dela kvadratrötter Steg 14

1. Bestäm om du har ett binomial i nämnaren. Nämnaren är talet i problemet du dividerar med. Ett binomium är ett polynom med två termer. Denna metod gäller endast divisionen av kvadratrötter som involverar ett binomial.

Till exempel om du $1 5 + \sqrt{2}$ ${frac{1}{5+{sqrt{2}}}}$ Om du vill räkna har du ett binomial i nämnaren, eftersom $5 + \sqrt{2}$ $5+{sqrt{2}}$ är ett polynom med två termer.

Bild med titeln Dela kvadratrötter Steg 15

2. Bestäm konjunktionen för binomialet. Konjugerade par är binomialer med samma termer men motsatta operatorer. Med hjälp av ett konjunktivpar kan du eliminera kvadratroten från nämnaren.

Till exempel,

5 + \sqrt{2}

$5+{sqrt{2}}$ och

5 - \sqrt{2}

$5-{sqrt{2}}$ är konjunktivpar, eftersom de har samma termer, men motsatta operatorer.

Bild med titeln Dela kvadratrötter Steg 16

3. Multiplicera täljaren och nämnaren med nämnarens konjunktion. Detta gör att du kan eliminera kvadratroten, eftersom produkten av ett konjugat par är skillnaden mellan kvadraten för varje term i binomialet. Det är,

(a - b) (a + b) = a 2 - b^{2}

$(a-b)(a+b)=a^{{2}}-b^{{2}}$ .

Till exempel:

1 5 + \sqrt{2}

${frac{1}{5+{sqrt{2}}}}$

= 1 (5 - \sqrt{2}) (5 + \sqrt{2}) (5 - \sqrt{2})

$={frac{1(5-{sqrt{2}})}{(5+{sqrt{2}})(5-{sqrt{2}})}}$

= 5 - \sqrt{2} (5 2 - (\sqrt{2})^{2}

$={frac{5-{sqrt{2}}}{(5^{{2}}-({sqrt{2}})^{{2}}}}$

= 5 + \sqrt{2} 25 - 2

$={frac{5+{sqrt{2}}}{25-2}}$

= 5 + \sqrt{2} 23

$={frac{5+{sqrt{2}}}{23}}$
Således,

1 5 + \sqrt{2} = 5 + \sqrt{2} 23

${frac{1}{5+{sqrt{2}}}}={frac{5+{sqrt{2}}}{23}}$ .

Tips

Många miniräknare har speciella funktioner för bråk. Ange koefficienten för täljaren, tryck på bråkknappen, ange sedan koefficienten för nämnaren. När du trycker på likhetstecknet efteråt borde räknaren ha skrivit om koefficienterna i minsta möjliga utsträckning.
Till skillnad från addition och subtraktion av rötter, i en bråkdel, behöver inte rötterna förenklas först för att ta bort kvadraterna. Faktum är att det ofta är bättre att inte göra detta.
Om du arbetar med kvadratrötter är oegentliga bråk lättare att lösa än blandade tal.

Varningar

Sätt aldrig en decimal i ett bråk. Det skulle annars vara en bråkdel inom en bråkdel.
Lägg aldrig ett decimaltal eller ett blandat tal före en rot, konvertera det till ett bråktal och förenkla hela uttrycket.
Lämna aldrig en kvadratrot i nämnaren för ett bråk, utan förenkla bråket.
Om nämnaren innehåller någon form av addition eller subtraktion, använd konjugatparmetoden för att ta bort radikalen från nämnaren.

"Dela kvadratrötter"

Multiplicera kvadratrötter

Förenkla kvadratrötter

Dela logaritmer

Dela bråk med bråk

Оцените, пожалуйста статью