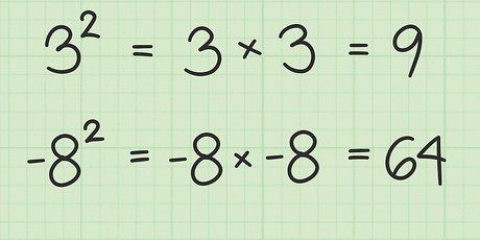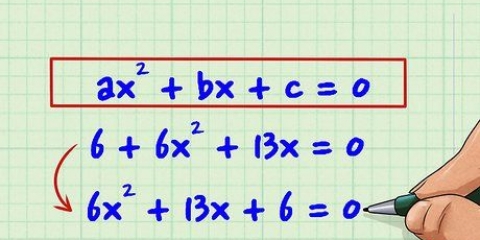Instrucțiuni gratuite pas cu pas 
Det enda undantaget från denna regel är själva talet 2, som, eftersom det är delbart med sig självt och 1, också är primtal. 2 är det enda jämna primtalet. 
Om vi till exempel vill använda den här metoden för att testa om 11 är primtal eller inte, måste vi dividera 11 med 3, 4, 5, 6, 7, 8, 9 och 10, varje gång vi letar efter ett heltalssvar utan rest. Eftersom inget av dessa tal passar helt in i 11 kan vi säga att 11 är a prime är. 
Låt oss undersöka faktorerna 100. 100 = 1 × 100, 2 × 50, 4 × 25, 5 × 20, 10 × 10, 20 × 5, 25 × 4, 50 × 2 och 100 × 1. Observera att efter 10 × 10 är faktorerna desamma som för 10 × 10, endast omvänt. I allmänhet kan vi ignorera faktorerna för n större än sqrt(n) eftersom de helt enkelt är en fortsättning på faktorer mindre än sqrt(n). Låt oss prova ett exempel. Om n = 37 behöver vi inte testa alla tal från 3 till 36 för att avgöra om n är primtal. Istället behöver vi bara titta på talen mellan 2 och sqrt(37) (avrundat uppåt). sqrt(37) = 6.08 – vi ska avrunda detta till 7. 37 är inte helt delbart med 3, 4, 5, 6 och 7 och så vi kan med säkerhet säga att det är en primtal är. 
Detta innebär att alla jämna faktorer, såväl som de som är multiplar av primtal, kan hoppas över. Låt oss till exempel försöka avgöra om 103 är primtal eller inte. Kvadratroten ur 103 är 11 (avrundat uppåt). Primtalen mellan 2 och 11 är 3, 5, 7 och 11. 4, 6, 8 och 10 är jämna och 9 är en multipel av 3, ett primtal, så vi kan hoppa över detta. Genom att göra detta minskade vi vår lista över möjliga faktorer till bara fyra siffror! 103 är inte helt delbart med 3, 5, 7 eller 11, så vi vet nu att 103 är en primtal är. 
Ett exempel: Är 100 ett primtal eller inte?. Anta att vi tar 3 som testvärde - detta är mellan 2 och n-1, så det räcker. 
En annan metod är att räkna ut a, och sedan dividera det med n, varefter du använder resten som ditt svar. Specialiserade miniräknare med en modulfunktion kan vara mycket användbara när man dividerar stora tal, eftersom de direkt kan beräkna resten av en division. Genom att använda en sådan kalkylator i vårt exempel kan vi se att 3/100 har en återstod av 1. Så, 3 (mod 100) är 1. 
I vårt exempel beräknar vi 3 med en modul på 100. 3 är ett väldigt, väldigt stort antal - 515,377,520,732,011,331,036,461,129,765,621,272,702,107,522,001 - så stort att det blir väldigt svårt att arbeta med. Istället för att använda det 48-siffriga svaret för 3, skulle vi hellre skriva det som en exponent, så ((((((3)*3))))*3)). Kom ihåg att att ta exponenten för en exponent ger effekten av att multiplicera exponenterna ((x) = x). Nu kan vi bestämma resten. Börja lösa för (((((((3)*3))))*3)) vid den inre uppsättningen av parenteser och arbeta dig utåt, dividera varje steg med 100. När vi har hittat resten använder vi det för nästa steg istället för som det faktiska svaret. Se nedan: ((((((9)*3))))*3)) - 9/100 har ingen rest, så vi kan fortsätta. (((((((27))))*3)) - 27/100 har ingen rest, så vi kan fortsätta. (((((729)))*3)) - 729/100 = 7 R 29. Vår återstod är 29. Vi går vidare till nästa steg, inte 729. ((((29=841))*3)) - 841/100 = 8 R 41. Vi använder återstoden 41 igen i nästa steg. (((41 = 1681)*3)) - 1681/100 = 16 R 81. Vi kommer att använda våra resterande 81 i nästa steg. ((81*3 = 243)) - 243/100 = 2 R 43. Vi använder våra resterande 43 i nästa steg. (43 = 1849) - 1849/100 = 18 R 49. Vi använder våra resterande 49 i nästa steg. 49 = 2401 - 2401/100 = 24 R 1. vår sista rest är 1. Med andra ord, 3 (mod 100) = 1. Observera att detta är samma svar som vi beräknade i föregående steg! 
I vårt exempel är 3 (mod 100) = 1 och 3 (mod 100) = 3. 1 ≠ 3, så vi kan säga att 100 är ett sammansatt tal. 
Anta att vi vill avgöra om n = 321 är ett primtal. 321 - 1 = 320, vilket vi kan uttrycka som 2×5. I detta fall är n = 321 ett lämpligt tal. Att bestämma n – 1 för n = 371 kan kräva ett stort värde för d, vilket gör hela processen svårare i ett senare skede. 371 - 1 = 370 = 2 × 185 
I vårt exempel med n = 321 väljer vi a = 100. 
I vårt exempel med n = 321, a (mod n) = 100 (mod 321). 100 = 10 000 000 000 (mod 321) = 313. Vi använder en speciell kalkylator, eller stenografimetoden med en exponent som beskrivits tidigare, för att hitta resten av 100/321. Eftersom vi inte fick 1 eller -1 kan vi inte med säkerhet säga att n är primtal. Men det finns mer vi behöver göra – läs vidare. 
Som en påminnelse, i vårt exempel är värdet på a lika med 100, värdet på s är 6 och på d5. Vi kommer att fortsätta med testning enligt nedan: 100 = 1×10. 1×10 (mod 321) = 64. 64 ` 1 eller -1. Håll dig lugn. 100 = 1×10. 1×10 (mod 321) = 244. 244 ≠ 1 eller -1. Vid det här laget kan vi sluta. s - 1 = 6 - 1 = 5. Vi har nu nått 4d = 2, och det finns inga potenser på 2 gånger d under 5d. Eftersom ingen av våra beräkningar gav en 1 eller -1 som svar, kan vi säga att n = 321 a sammansatt nummer är. 
Data1 = 1 Data2 = 2 
Beräkna MMI MMI1 = Test Number2 ^ -1 Mod Test Number1 MMI2 = Test Number1 ^ -1 Mod Test Number2 Endast för primtal (det kommer att finnas ett resultat för icke-primtal, men det är inte MMI): MMI1 = (TestNumber2 ^ (TestNumber1-2)) %TestNumber1 MMI2 = (Testnummer1 ^ (Testnummer-2)) % Testnummer2 Så: MMI1 = (97^33) %35 MMI2 = (35^95) %97 
För MMI1 F(1) = Testnummer2 % Testnummer1 = 97 % 35 = 27 F(2) = F(1) * F(1) % Testnummer1 = 27 * 27 % 35 = 29 F(4) = F(2) * F(2) % Testnummer1 = 29 * 29 % 35 = 1 F(8) = F(4) * F(4) % Testnummer1 = 1 * 1 % 35 = 1 F(16) =F(8) * F(8) % Testnummer1 = 1 * 1 % 35 = 1 F(32) = F(16) * F(16) % Testnummer1 = 1 * 1 % 35 = 1 Beräkna den binära logaritmen för Testnummer1 - 2 35 -2 = 33 (10001) bas 2 MMI1 = F(33) = F(32) * F(1) mod 35 MMI1 = F(33) = 1 * 27 Mod 35 MMI1 = 27 För MMI2 F(1) = Testnummer1 % Testnummer2 = 35 % 97 = 35 F(2) = F(1) * F(1) % Testnummer2 = 35 * 35 mod 97 = 61 F(4) = F(2) * F(2) % Testnummer2 = 61 * 61 mod 97 = 35 F(8)= F(4) * F(4) % Test Number2 = 35 * 35 mod 97 = 61 F(16) = F(8) * F(8) % Testnummer2 = 61 * 61 mod 97 = 35 F(32)= F(16) * F(16) % Testnummer2 = 35 * 35 mod 97 = 61 F(64)= F(32) * F(32) % Test Number2 = 61 * 61 mod 97 = 35 F(128) = F(64) * F(64) % Testnummer2 = 35 * 35 mod 97 = 61 Beräkna den binära logaritmen för TestNumber2 - 2 97 - 2 = 95 = (1011111) bas 2 MMI2 = (((((F(64) * F(16) % 97) * F(8) % 97) * F(4) % 97) * F(2) % 97) * F(1) % 97 ) MMI2 = ((((((35 * 35) %97) * 61) % 97) * 35% 97) * 61% 97) * 35% 97) MMI2 = 61 
Svar = (1 * 97 * 27 + 2 * 35 * 61) % (97 * 35) Svar = (2619 + 4270) % 3395 Svar = 99 
Beräkna (Svar - Data1) % Testnummer1 99 -1 % 35 = 28 Eftersom 28 är större än 0 är 35 inte primtal 
Beräkna (Svar - Data2) % Testnummer2 99 - 2 % 97 = 0 Eftersom 0 är lika med 0, är 97 ett potentiellt primtal 
Om steg 7 är lika med 0: Använd en annan "test nummer 1" om TestNumber1 inte är primtal. Använd ett annat TestNumber1 där ett TestNumber1 faktiskt är ett primtal.I det här fallet är steg 6 och 7 lika med 0. Använd olika datapunkter för data1 och data2. Om steg 7 alltid är lika med 0, är sannolikheten att tal2 är primtal mycket hög. Steg 1 till 7 är kända för att vara felaktiga i vissa fall när det första talet inte är primtal och det andra är en primtalsfaktor av icke-primtal "test nummer 1".Det fungerar i alla scenarier där båda talen är primtal. Anledningen till att steg 1 till 7 upprepas beror på att det finns några scenarier där, även om TestNumber1 inte är primtal och TestNumber2 inte är primtal, är något av talen från steg 7 fortfarande noll.Dessa tillstånd är sällsynta.Genom att ändra TestNumber1 till ett annat icke-primtal, om TestNumber2 inte är primtal, kommer TestNumber2 inte längre att vara lika med noll, i steg 7. Med undantag för det fall där "test nummer 1" är en faktor av TestNumber2, kommer primtal alltid att vara noll i steg 7.
Kontrollera om ett tal är primtal
Primtal är tal som bara är delbara med sig själva och kallas 1 – andra tal förening tal. När det gäller att testa om ett tal är primtal finns det flera alternativ. Vissa av dessa metoder är relativt enkla men definitivt inte praktiska för större antal. Andra tester som ofta används är faktiskt kompletta algoritmer baserade på en sannolikhet som ibland av misstag klassificerar ett tal som primtal. Läs vidare i steg 1 för att lära dig hur du testar dig själv om du har att göra med ett primtal.
Steg
Metod 1 av 4: Prova genom att dividera
Att försöka genom att dividera är det absolut enklaste sättet att testa ett tal. För små nummer är det vanligtvis också det snabbaste sättet. Testet baseras på definitionen av ett primtal: ett tal är primtal om det bara är delbart med sig självt och 1.
1. Par n är numret du vill testa. Dividera talet n med alla möjliga delbara heltal. För större tal som n=101 är det extremt opraktiskt att dividera med alla möjliga heltal mindre än n. Lyckligtvis finns det flera knep för att minska antalet faktorer som ska testas.
2. Bestämma huruvida n till och med är. Alla jämna tal är helt delbara med 2. Därför, om n är jämnt, kan du säga det n är ett sammansatt tal (och därför inte ett primtal). För att snabbt avgöra om ett tal är jämnt behöver du bara vara uppmärksam på den sista siffran. Om den sista siffran är 2, 4, 6, 8 eller 0, är talet jämnt och inte primtal.
3. Del n med valfritt tal mellan 2 och n-1. Eftersom ett primtal inte har några andra faktorer än sig själv och 1 och eftersom heltalsfaktorer är mindre än deras produkt, kommer en kontroll av delbarheten för ett heltal mindre än n och större än 2 att avgöra om n är primtal. Vi börjar efter 2 eftersom jämna tal (multiplar av 2) inte kan vara primtal. Detta är långt ifrån ett effektivt sätt att testa, som du kommer att se nedan.
4. För att spara tid testa endast upp till sqrt(n), avrundat uppåt. Att testa ett nummer n genom att kontrollera alla siffror mellan 2 och n-1 kan snabbt bli väldigt tidskrävande. Om vi till exempel vill kontrollera om 103 är primtal med den här metoden, måste vi dividera med 3, 4, 5, 6, 7 ... etc., ända till 102! Lyckligtvis är det inte nödvändigt att testa så här. I praktiken är det bara nödvändigt att testa med faktorerna mellan 2 och kvadratroten ur n. Om kvadratroten ur n inte är ett tal, avrunda det till närmaste heltal och testa till detta tal. Se nedan för en förklaring:
5. För att spara ännu mer tid använder vi bara primtal factors. Det är möjligt att göra processen att testa genom division ännu kortare genom att inte inkludera de faktorer som inte är primtal. Per definition kan vilket sammansatt tal som helst uttryckas som produkten av två eller flera primtal. Så att dividera talet n med ett sammansatt tal är onödigt - det motsvarar att dividera med primtal flera gånger. Så vi kan ytterligare begränsa listan över möjliga faktorer till endast primtal mindre än sqrt(n).
Metod 2 av 4: Använder Fermat .s lilla teorem
År 1640 ställde den franske matematikern Pierre de Fermat först en sats (som nu är uppkallad efter honom) som kan vara till stor hjälp för att avgöra om ett tal är primtal eller inte. Tekniskt sett är Fermats test tänkt att kontrollera om ett tal är sammansatt, snarare än primtal. Detta beror på att testet med "absolut säkerhet" kan visa att ett tal är sammansatt, men bara en "sannolikhet" om ett tal är primtal. Fermats lilla sats är användbar i situationer där det inte är praktiskt att försöka dividera med och när en lista med tal finns tillgänglig som är undantag från satsen.
1. Anta n numret är för testning. Du använder detta test för att avgöra om ett givet tal n är primtal. Men som nämnts ovan kan denna sats ibland felaktigt karakterisera vissa kompositer som primtal. Det är viktigt att ta hänsyn till detta och kontrollera ditt svar, som kommer att förklaras senare.
2. Välj ett heltal a mellan 2 och n-1 (inklusive). Det exakta heltal du väljer är inte viktigt. Eftersom parametrarna för a är inklusive 2 och n-1 kan du även använda dessa.
3. Beräkna a (mod n). Att arbeta fram detta uttryck kräver viss kunskap om ett matematiskt system som kallas modulär matematik. I modulär matematik återgår siffror till noll när de når ett visst värde, känt som modul. Du kan tänka på det här som en klocka: så småningom kommer klockvisaren att skjuta tillbaka till klockan 1 efter klockan 12, inte till klockan 1. Modulen är noterad som (mod n). Så i detta steg räknar du med en modul på n.
4. Om vi räknar ut detta för hand använder vi exponenten som kort notation. Om du inte har en miniräknare med en modulfunktion, använd exponentiell notation för att göra proceduren för att bestämma resten enklare. Se nedan:
5. Kolla om a (mod n) = a (mod n). Om inte, är n sammansatt. Om sant är n förmodligen, (men inte säker) ett primtal. Att upprepa testet med olika värden för a kan göra resultatet säkrare, men det finns sällsynta sammansatta tal som uppfyller Fermats teorem för Allt värden på a. Dessa kallas Carmichael-talen - det minsta av dessa nummer är 561.
6. Använd Carmichael-siffrorna för att vara säker på ditt resultat. Att veta vilka siffror som uppfyller Carmichael-sekvensen innan du fortsätter kan spara dig mycket huvudvärk om huruvida ett tal är primtal eller inte. I allmänhet är Carmichael-tal produkten av individuella primtal, där det för alla primtal gäller att om p är en divisor av n, så är p-1 också en divisor av n-1. Onlinelistan över Carmichael-tal kan vara mycket användbar för att avgöra om ett tal är primtal med hjälp av Fermats lilla teorem.
Metod 3 av 4: Användning av Miller-Rabin-testet
Miller-Rabin-testet fungerar på samma sätt som Fermats lilla teorem, men hanterar anomala tal som Carmichael-tal på ett bättre sätt.
1. Par n är ett udda tal som vi vill testa för primalitet. Liksom i de ovan angivna metoderna är n den variabel vi vill bestämma primaliteten för.
2. Upptagen n-1 rabatt i formen 2 × d varigenom d är udda. Talet n är primtal om det är udda. Så n - 1 måste vara jämnt. Eftersom n - 1 är jämnt kan det skrivas som en potens av 2 gånger ett udda tal . Så,4 = 2 × 1; 80 = 2 x 5; och så vidare.
3. Välj valfritt nummer a mellan 2 och n-1. Det exakta antalet du väljer spelar ingen roll - bara att det måste vara mindre än n och större än 1.
4. Beräkna a (mod n). om a = 1 eller -1 (mod n), sedan motstårn Miller-Rabin-testet och är förmodligen ett primtal. Precis som med Fermats lilla sats kan detta test inte bestämma primaliteten för ett tal med absolut säkerhet, utan behöver ytterligare tester för att göra det.
5. Eftersom resultatet inte är lika med 1 eller -1, beräknaa, a,... och så vidare, upp till ad. Beräkna a till makten av d gånger, upp till 2. Om en av dessa är lika med 1 eller -1 (mod n), sedan motstår n Miller-Rabin-testet och är förmodligen prime. När du har fastställt att n klarar testet, kontrollera sedan ditt svar (se steget nedan). Om n inte klarar något av dessa prov är det a sammansatt siffra.
6. om n uppfyller Miller-Rabin-testet, upprepa sedan för de andra värdena av a. Om du har upptäckt att värdet på n mycket väl kan vara primtal, försök igen med ett annat slumpmässigt värde för a för att bekräfta resultatet av testet. Om n faktiskt är primtal, kommer detta att gälla för vilket värde som helst av a. Om n är ett sammansatt tal, kommer det att misslyckas under tre fjärdedelar av värdena på a. Detta ger dig mer säkerhet än med Fermats lilla teorem, där vissa sammansatta tal (Carmichael-talen) klarar testet för varje värde av en.
Metod 4 av 4: Använd den kinesiska restsatsen
1. Välj två nummer. Ett av talen är inte primtal och det andra är talet som testas för primalitet.
- "test nummer 1" = 35
- Test nummer2 = 97
2. Välj två datapunkter större än noll och mindre än TestNumber1, respektive TestNumber2. De kan inte vara likadana.
3. Beräkna MMI (Mathematical Multiplicative Inverse) för TestNumber1 och TestNumber2
4. Skapa en binär tabell för varje MMI upp till Log2 av modulen
5. Beräkna (Data1 * TestNumber2 * MMI1 + Data2 *TestNumber1 * MMI2) % (TestNumber1 * TestNumber)
6. Kolla om "test nummer 1" är inte prime 1
7. Kontrollera om TestNumber2 är ett primtal
8. Upprepa steg 1 till 7 minst två gånger till.
Tips
- De 168 primtal under 1000 är: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79 , 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157. , 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 314, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 7 , 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461. , 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619. , 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 812, 8, 812, 8, 8, 3 , 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 913, 9
- När man försöker dividera är långsammare än de mer sofistikerade metoderna, är det fortfarande effektivt för mindre tal. Även när man testar större siffror är det inte ovanligt att man kontrollerar de små siffrorna först innan man byter till de mer avancerade metoderna.
Förnödenheter
- Papper, penna, penna och/eller en miniräknare för att träna
"Kontrollera om ett tal är primtal"
Оцените, пожалуйста статью
