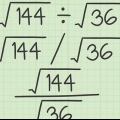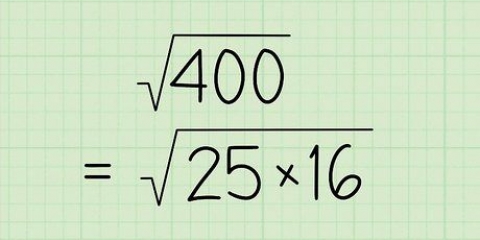Ett annat exempel: Vi vill hitta kvadratroten ur 25 (√(25)). Det betyder att vi måste hitta talet som multiplicerat med sig självt har 25 som produkt. Eftersom 5 = 5 × 5 = 25, kan vi säga att √(25) = 5. Du kan också tänka på detta som att "ångra" en kvadrat (eller potensnummer). Om vi till exempel vill hitta kvadratroten ur 64 (√64), betrakta 64 som 8 . först. Eftersom en radikal i princip `eliminerar` en kvadrat kan vi säga att √(64) = √(8) = 8. 
Å andra sidan kallas tal som inte ger heltal efter kvadratrot, ofullkomlig kvadrat. När du tar kvadratroten ur ett av dessa tal får du vanligtvis en decimal eller bråktal. Ibland kan de inblandade decimalerna bli riktigt röriga. Till exempel, √(13) = 3,605551275464.. 
1 = 1 × 1 = 1 2 = 2 × 2 = 4 3 = 3 × 3 = 9 4 = 4 × 4 = 16 5 = 5 × 5 = 25 6 = 6 × 6 = 36 7 = 7 × 7 = 49 8 = 8 × 8 = 64 9 = 9 × 9 = 81 10 = 10 × 10 = 100 11 = 11 × 11 = 121 12 = 12 × 12 = 144 
Anta att du vill beräkna kvadratroten av 900. Vid första anblicken ser detta väldigt svårt ut! Det är dock inte svårt om vi räknar in 900. "Faktorer" är de siffror som kan multiplicera tillsammans för att göra ett annat tal. Till exempel, eftersom 6 är produkten av 1 × 6 och 2 × 3, är faktorerna för 6 talen 1, 2, 3 och 6. Istället för att räkna med talet 900, vilket är lite obekvämt, skriver vi det som 9 × 100. Nu, eftersom 9 är en perfekt kvadrat och skild från 100, kan vi ta dess kvadratrot. √(9 × 100) = √(9) × √(100) = 3 × √(100). Med andra ord, √(900) = 3√(100). Vi kan förenkla dessa två steg ytterligare genom att dela upp 100 i faktorerna 25 och 4. √(100) = √(25 × 4) = √(25) × √(4) = 5 × 2 = 10. Så vi kan säga att √(900) = 3(10) = 30. 
Obs: Även om imaginära tal inte kan representeras med vanliga tal, kan de fortfarande behandlas som vanliga tal på många sätt. Till exempel kan rötterna av negativa tal kvadreras för att ge dessa negativa tal precis som vilken annan kvadratrot som helst. Till exempel: i = -1. 

I vårt exempel delar vi 6,45 i par så här: 6-,45-00. Observera att det finns ett "återstående" nummer till vänster &mdash det är poängen. 
I vårt exempel är den första gruppen i 6-,45-00 6:an. Det största antalet mindre än eller lika med 6 är 2 — 2 = 4. Skriv en `2` ovanför 6:an under radikalen. 
I vårt exempel börjar vi med det dubbla av 2, den första siffran i vårt svar. 2 × 2 = 4. Sedan subtraherar vi 4 från 6 (vår första `grupp`) och vi får 2 som svar. Sedan flyttar vi nästa grupp (45) ner en rad för att få 245. Slutligen skriver vi ytterligare 4 till vänster, och lämnar lite utrymme att lägga till i slutet, så här: 4_. 
I vårt exempel letar vi efter numret för att fylla i det tomma fältet 4_ × _; det gör svaret så stort som möjligt, men ändå mindre än eller lika med 245. I det här fallet är svaret 5. 45 × 5 = 225, medan 46 × 6 = 276. 
Vi fortsätter med vårt exempel och fortsätter med 225 - 245 = 20. Sedan tar vi ner nästa siffror, 00, för att bli 2000. Om vi dubblar talet ovanför radikalen får vi 25 × 2 = 50. Vi löser det okända i 50_ × _ =/< 2000, då får vi 3 som ett svar. Vid denna tidpunkt har vi `253` ovanför radikalen — upprepar vi detta igen, 9 är nästa siffra. 
I vårt exempel är siffran under det radikala tecknet 6,45, så vi flyttar helt enkelt decimalkomma uppåt och placerar den mellan 2 och 5 av vårt svar, vilket ger oss 2,539 ger. 

I vårt exempelproblem är en rimlig uppskattning för kvadratroten av 40 kanske 6.4, eftersom vi från ovanstående vet att svaret förmodligen är något närmare 6 än 7. 
Multiplicera 6,4 med sig själv, så 6,4 × 6,4 = 40,96, som är något större än det ursprungliga antalet. Sedan multiplicerar vi talet med en tiondel mindre än vår uppskattning ovan (eftersom vårt svar var för högt), och vi får 6,3 × 6,3 = 39,69. Detta är något lägre än vårt ursprungliga antal. Det betyder att kvadratroten ur 40 är någonstans mellan 6,3 och 6,4 lögner. Dessutom, eftersom 39,69 är närmare 40 än 40,96, vet du att kvadratroten är närmare 6,3 än 6,4. 
I vårt exempel, låt oss välja 6,33 för vår gissning med två decimaler. Kvadratur 6,33 och du får 6,33 × 6,33 = 40,0689. Eftersom detta är något över vårt ursprungliga nummer kommer vi att prova ett något lägre nummer, till exempel 6,32. 6,32 × 6,32 = 39,9424. Detta är något under vårt ursprungliga antal, så vi vet att den exakta kvadratroten mellan 6.33 och 6.32 lögner. Om vi ville gå längre kan vi fortsätta använda samma tillvägagångssätt för att få ett svar som blir mer och mer korrekt.
Lös kvadratrötter
Även om den skrämmande synen av en kvadratrotssymbol kan få människor med matematikångest att krypa, är kvadratrotproblem inte så svåra att lösa som de verkar vid första anblicken. Enkla kvadratrotsproblem kan ofta lösas lika enkelt som enkla multiplikations- och divisionsproblem. Mer komplexa kvadratrotsproblem å andra sidan kan kräva lite mer arbete, men med rätt tillvägagångssätt kan även dessa problem lösas enkelt. Börja öva kvadratrotsproblem idag för att lära dig den här matematiska färdigheten som kan vara ny för dig!
Steg
Del 1 av 3: Förstå krafter och rötter

1. Kvadra ett tal genom att multiplicera det med sig självt. För att förstå rötter är det bäst att börja med rutorna. Kvadrater är lätta - att kvadrera ett tal motsvarar att multiplicera det med sig självt. Till exempel: 3 i kvadrat är detsamma som 3 × 3 = 9, och 9 i kvadrat är samma som 9 × 9 = 81. Kvadrater indikeras med en liten "2" ovanför och till höger om talet i kvadrat - så här: 3, 9, 100, etc.
- Prova att kvadrera några siffror själv för att testa detta koncept. Kom ihåg att att kvadrera ett tal inte är något annat än att multiplicera det talet med sig självt. Du kan göra detta även med negativa tal. I alla fall kommer svaret alltid att vara positivt. Till exempel: -8 = -8 × -8 = 64.

2. För att hitta roten till ett tal, hitta "inversen av" en kvadrat. Symbolen för kvadratroten (√, även känd som "radikaltecknet") är i princip "motsatsen" till kvadratsymbolen (). Om du ser ett radikalt tecken kan du fråga dig själv: `Vilket tal kan jag multiplicera med sig själv så att jag får talet under det radikala tecknet??` Till exempel: om du ser kvadratroten √(9), så letar du efter talet som multiplicerat med sig självt har nio som produkt. I det här fallet alltså tre, eftersom 3 = 9.

3. Vet skillnaden mellan perfekta och imperfekta rutor. Fram till nu var svaren på kvadratrotsproblemen fina, runda tal. Detta är inte alltid fallet - i själva verket finns det svar på kvadratrötter som är mycket långa, besvärliga decimaltal. Rottal som är heltal (med andra ord tal som inte är bråktal eller decimaler) kallas rutor. Alla ovanstående exempel (9, 25 och 64) är kvadrater (även kallade perfekta kvadrater), för genom att ta kvadratrötter får vi heltal (3, 5 och 8) som ett resultat.

4. Memorera de första 10-12 rutorna. Som du säkert har märkt är kvadratrötter eller kvadrater ofta väldigt lätta! Eftersom dessa matematiska problem är så enkla, är det värt din tid att lära dig rötterna till de första 12 eller fler kvadraterna. Du kommer att stöta på dessa siffror mycket, så du kan spara mycket tid i det långa loppet genom att lära dig dem tidigt. De första 12 rutorna är:

5. Förenkla rötter genom att ta bort rutor där det är möjligt. Att hitta rötterna till ofullkomliga rutor kan ibland vara knepigt - speciellt om du inte använder en miniräknare (styckena nedan ger dig knep för att göra processen enklare). Det är dock ofta möjligt att förenkla siffrorna under det radikala tecknet, för att underlätta arbetet med dem. För att göra detta behöver du bara faktorisera talet under radikalen, sedan ta kvadratroten av faktorer som är kvadrater och skriva svaret utanför radikalen. Det här är enklare än det låter – läs vidare för att lära dig mer!

6. Använd imaginära tal för rötterna till negativa tal. Vilken kvadrat är -16? Det är inte 4 eller -4 — att kvadrera båda ger 16 (positivt). Vet du inte? Det finns faktiskt inget sätt att skriva kvadratroten ur -16 eller något negativt tal med vanliga tal. I dessa fall måste vi använda imaginära siffror (vanligtvis i form av bokstäver eller symboler) för att ersätta kvadratroten av det negativa talet. Till exempel, variabeln `i` används vanligtvis för kvadratroten av -1. Som en allmän regel kommer kvadratroten ur ett negativt tal alltid att vara ett imaginärt tal (eller innehålla ett).
Del 2 av 3: Använda långdivisionsalgoritmer

1. Beställ ditt kvadratrotsproblem som lång division. Även om det kan vara lite tidskrävande, är det möjligt att beräkna rötterna till svåra imperfekta kvadrater utan en miniräknare. För att göra detta använder vi en lösningsmetod (eller algoritm) som liknar - men inte exakt samma som - en lång division.
- Skriv först ner kvadratroten på samma sätt som lång division. Låt oss till exempel säga att vi vill beräkna kvadratroten ur 6,45, vilket verkligen inte är en lämplig perfekt kvadrat. Först skriver vi en vanlig radikalsymbol (√), sedan skriver vi talet under den. Därefter ritar vi en linje ovanför numret så att det är i en liten "låda" - precis som lång division. När vi är klara noterade vi ett avlångt `√` med 6,45 under.
- Vi skriver siffror ovanför problemet, så lämna lite utrymme.

2. Gruppera siffrorna i par. För att lösa ditt problem, gruppera siffrorna i numret under det radikala tecknet i par, med början från decimalkomma. Du kan lägga till små markeringar (som punkter, snedstreck, kommatecken osv.) mellan dina par för att skilja dem åt.

3. Hitta det största talet vars kvadrat är mindre än eller lika med den första `gruppen`. Börja med det första numret eller paret till vänster. Välj det största talet med en kvadrat som är mindre än eller lika med "gruppen". Till exempel, om gruppen är 37, skulle du välja 6, eftersom 6 = 36 (mindre än 37), men 7 = 49 (större än 37). Skriv detta nummer ovanför den första gruppen. Detta är den första siffran i ditt svar.

4. Dubbla talet du nyss skrev ner, skriv det under den första gruppen och subtrahera det. Ta den första siffran i ditt svar (numret du just hittade) och dubbla det. Skriv detta under din första grupp och subtrahera det för att hitta skillnaden. Placera nästa nummerpar bredvid svaret nedan. Skriv slutligen den sista siffran av dubbelt den första siffran i ditt svar till vänster, lämna lite utrymme bredvid den.

5. Fyll det tomma utrymmet. Därefter är avsikten att lägga till en siffra till höger om numret som du har skrivit till vänster. Välj ett tal som multipliceras med ditt nya tal ger den största möjliga produkten, men ändå är mindre än eller lika med det "neddragna" talet. Till exempel, om ditt "neddragna" tal är 1700 och siffran till vänster är 40_, skulle du fylla i det tomma med "404" eftersom 404 × 4 = 1616 (mindre än 1700), medan 405 × 5 = 2025. Numret du hittar i det här steget är den andra siffran i ditt svar, så du kan lägga till det ovanför radikalen.

6. Fortsätt att använda dina "tomma" siffror för ditt svar. Fortsätt med den här modifierade långa divisionen tills du får nollor när du subtraherar "draw down"-talet, eller så har du uppnått önskad noggrannhet. När du är klar är siffrorna du använde för att fylla de tomma fälten i varje steg (plus den allra första siffran du använde) siffrorna i ditt svar.

7. Flytta decimaltecknet för din ursprungliga "divisor" uppåt. För att avrunda ditt svar måste du sätta kommatecken (decimaltecknet) på rätt plats. Lyckligtvis är detta enkelt - allt du behöver göra är att justera det med decimaltecknet i ditt ursprungliga nummer. Om talet under radikalen är 49,8 flyttar du decimalkomma upp mellan de två talen över 9 och 8.
Del 3 av 3: Uppskatta imperfekta rutor snabbt

1. Hitta ofullkomliga rutor genom att uppskatta. När du har memorerat dina rutor blir det mycket lättare att hitta rötterna till ofullkomliga rutor. Eftersom du redan kan ett dussin rutor, kan alla tal som faller mellan två av dessa perfekta kvadrater hittas genom att uppskatta mellan dessa värden. För att börja, hitta de två rutor som ditt nummer hamnar mellan. Bestäm sedan vilken av dessa två rutor som är närmast talet.
- Anta till exempel att vi behöver hitta kvadratroten ur 40. Eftersom vi har memorerat våra rutor kan vi säga att 40 hamnar mellan 6 och 7, eller 36 och 49. Eftersom 40 är större än 6 kommer dess kvadratrot att vara större än 6, och eftersom den är mindre än 7 kommer dess kvadratrot att vara mindre än 7. Siffran 40 är lite närmare 36 än 49, så svaret kommer förmodligen att vara lite närmare 6. I nästa steg kommer vi att göra vårt svar mer exakt.

2. Beräkna kvadratroten till en decimal. När du väl har valt två rutor som ditt nummer ligger mellan är det bara att uppskatta tills du hittar ett svar du är nöjd med. Ju längre du kommer, desto mer exakt är ditt svar. För att börja, välj en tio för ditt svar - det behöver inte vara korrekt, men du sparar tid om du använder sunt förnuft genom att välja en siffra som är nära det korrekta svaret.

3. Multiplicera uppskattningen med sig själv. Sedan kvadrerar du uppskattningen. Om du inte har tur kommer du förmodligen inte att få ditt ursprungliga nummer - du kommer antingen att hamna något högre eller lägre. Om ditt svar är för högt, försök igen med en lite mindre uppskattning (och vice versa om det är för lågt).

4. Fortsätt att uppskatta om det behövs. Om du är nöjd med dina svar kanske du bara vill använda en av dina första gissningar. Men om du vill ha ett mer exakt svar behöver du bara välja en uppskattning för din "hundring" som placerar denna uppskattning mellan dina två första. Om du fortsätter med det här mönstret kan du få ett svar med tre, fyra eller fler decimaler — det beror bara på hur långt du vill gå.
Tips
- Använd en miniräknare för snabba lösningar. De flesta moderna miniräknare kan beräkna kvadratrötter direkt. Vanligtvis behöver du bara ange ditt nummer och sedan trycka på knappen med radikalen i andra potensen (kvadratroten). Till exempel, för att hitta kvadratroten av 841, tryck på följande tangenter: 8, 4, 1, (√) och gör rätt 29 på som svar.
Оцените, пожалуйста статью