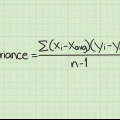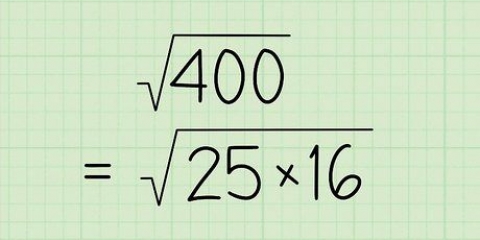Hur man beräknar Spearmans rankkorrelationskoefficient

Steg
Tips
Varningar

Med Spearmans rangkorrelationskoefficient kan du se om två variabler är relaterade av en monoton funktion (d.w.z. att om ett nummer ökar så ökar också det andra talet eller vice versa). För att beräkna Spearmans rankkorrelationskoefficient måste du beställa och jämföra datamängder för att hitta Σd och sedan ange det värdet i standardversionen eller den förenklade versionen av Spearmans rankkorrelationskoefficientformel. Du kan också beräkna denna koefficient med Excel-formler eller R-kommandon.

Steg

Metod 1 av 3: Manuellt

1. Rita din datatabell. Ordnar informationen du behöver för att beräkna Spearmans rankkorrelationskoefficient. Du behöver:

6 kolumner med rubriker, som visas ovan.
Så många rader som du har datapar.

2. Fyll de två första kolumnerna med dina datapar.

3. Ordna datapunkterna i den första kolumnen i den tredje kolumnen, från 1 till n (det totala antalet datapunkter du har). Ge den lägsta siffran position 1, nästa nummer position 2, och så vidare.

4. Gör samma sak med den fjärde kolumnen som i steg 3, men ordna nu den andra kolumnen.

Om du har två (eller fler) datapunkter med samma värde i en kolumn, ta medelvärdet av positionerna som dessa datapunkter normalt skulle ha och ge datapunkterna detta medelvärde som deras nya position.
I exemplet till höger finns två femmor som normalt skulle vara i position 2 och 3. Det är två samma låtar, alltså ta genomsnittet av sina positioner. Medelvärdet av 2 och 3 är 2,5, så ge båda femmorna position 2,5.

5. I kolumnen `d` beräknar du skillnaden mellan de två positionerna i varje datapar. Med andra ord, om den ena har position 1 och den andra har position 3, är skillnaden 2. (Positiv eller negativ spelar ingen roll, eftersom vi kommer att räta upp denna skillnad i nästa steg.)

6. Kvadratera värdena i d-kolumnen och skriv dessa värden i d-kolumnen.

7. Lägg ihop alla datapunkter i kolumnen d. Detta värde är Σd.

8. Välj en av formlerna nedan:

Om inga lika datapunkter inträffade i de föregående stegen, skriv in Σd i den enkla formeln för Spearmans rangkorrelationskoefficient

och ange antalet datapar för `n` för att hitta ditt svar.

Om liknande datapunkter förekom i de föregående stegen, använd standardformeln för Spearmans rangkorrelationskoefficient:

9. Tolka resultatet. Detta kan variera mellan -1 och 1.

Nära -1 – Negativ korrelation.

Nära 0 – Ingen linjär korrelation.

Nära 1 – Positiv korrelation.

Metod 2 av 3: I Excel

1. Skapa nya kolumner med positionerna för de befintliga kolumnerna. Till exempel, om du har dina data i kolumn A2:A11, skulle du använda formeln `=RANK(A2,A$2:A$11)` och utöka intervallet över alla dina rader och kolumner.

2. Behandla lika datapunkter enligt beskrivningen i steg 3 och 4 i metod 1.

3. I en ny cell gör du en korrelationsberäkning mellan de två kolumnerna med en formel som `=CORREL(C2:C11,D2:D11)`. I detta fall är C och D positionskolumnerna. Spearmans rangkorrelationskoefficient visas i korrelationscellen.

Metod 3 av 3: Med R

1. Installera R om du inte redan har det. (Ser https://www.r-projekt.org/.)

2. Spara dina data som en CSV-fil, med de data du vill korrelera i de två första kolumnerna. Du kan göra detta med menyn `Spara som`.

3. Öppna R-editorn. Om du arbetar i terminalen, kör bara R. När du är på skrivbordet klickar du på R-logotypen.

4. Skriv följande kommandon:

d <- läsa.csv("NAME_OF_YOU_CSV.csv") och tryck på enter

cor(rank(d[,1]),rank(d[,2]))

Tips

För de flesta datamängder behöver du minst fem datapar för att fastställa en trend (endast tre par användes i exemplet för att göra exemplet enklare).

Varningar

Spearmans rankkorrelationskoefficient visar bara korrelationsstyrkan om datapunkterna kontinuerligt ökar eller minskar. Om spridningsdiagrammet för datapunkterna visar en annan trend, kommer Spearmans rangkorrelationskoefficient att öka korrelationen inte visas korrekt.
Denna formel är baserad på antagandet att det inte finns lika datapunkter. Om det finns lika datapunkter, som i exemplet ovan, använd följande definition: produkt-moment-korrelationskoefficienten för leden.