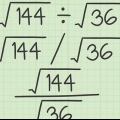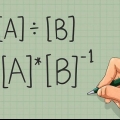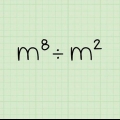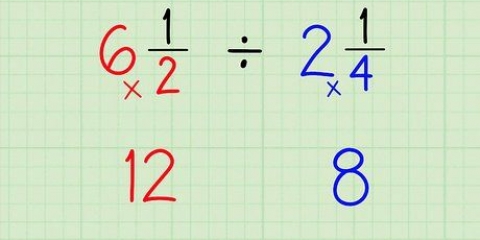Exempel 1: Lös:  .
.
Börja med att konvertera detta till en logaritm med formeln ovan: .
. Denna formel är "förändring av bas"-formeln, härledd från de grundläggande logaritmiska egenskaperna. 
Exempel 1 (forts.): Skriva om  om
om  . Värdet av `?` är svaret på problemet. Du kanske måste prova några för att hitta den:
. Värdet av `?` är svaret på problemet. Du kanske måste prova några för att hitta den:



16 är vad du letade efter, så = 4.
= 4. 
Exempel 2: Vad är  ?
? Konvertera detta till en logaritm::  .(Observera att 3 försvinner i alla inledande loggar -- detta gäller alla baser).
.(Observera att 3 försvinner i alla inledande loggar -- detta gäller alla baser). Skriv om som  och testa möjliga värden på ?:
och testa möjliga värden på ?:


Eftersom 58 hamnar mellan dessa två siffror har inget heltal som svar.
inget heltal som svar. Lämna ditt svar som:  .
. 

Om antingen x eller y är negativ, det finns ingen lösning på problemet. om både x om y är negativ, ta bort de negativa tecknen med hjälp av egenskapen 
Det finns inga logaritmer för negativa tal i exemplet, så du kan gå vidare till nästa steg. 
Använd detta för att expandera den vänstra sidan av exempelproblemet:

Byt tillbaka detta till den ursprungliga ekvationen:

→


Exempelproblemet har en ny term:  . Eftersom 3 = 27, förenkla
. Eftersom 3 = 27, förenkla  otäck 3.
otäck 3. Den fullständiga jämförelsen är nu:




 .
.
I exemplet problemet n fortfarande fångad i termen  .
.
Runt n för att isolera, använd produktregeln för logaritmer:

Byt tillbaka detta till hela ekvationen:





Sedan 3 = 19683, n =19683
Dela logaritmer
Logaritmer kan se svåra att använda, men precis som exponenter eller polynom måste du bara lära dig rätt tekniker. Du behöver bara känna till några grundläggande egenskaper för att dela två logaritmer med samma bas, eller för att utöka en logaritm med en kvot.
Steg
Metod 1 av 2: Dela logaritmer för hand

1. Kontrollera om det finns negativa siffror och ettor. Denna metod hanterar problem i formuläret  . Det fungerar dock inte för några speciella fall:
. Det fungerar dock inte för några speciella fall:
 . Det fungerar dock inte för några speciella fall:
. Det fungerar dock inte för några speciella fall: - Logaritmen för ett negativt tal är inte definierad för alla baser (som t.ex
eller
). Skriv sedan "Ingen lösning".
- Logaritmen för noll är också odefinierad för alla baser. Om du ser en term som
, skriv sedan även "Ingen lösning".
- Logaritmen för en i valfri bas (
) är alltid lika med noll, eftersom
för alla värden av X. Ersätt den logaritmen med 1 istället för att använda metoden nedan.
- Om de två logaritmerna har olika baser, som t.ex
, och du kan inte förenkla någon av dem till ett heltal, då kan problemet inte lösas för hand.

2. Redigera uttrycket i en logaritm. Förutsatt att du inte hittade något av ovanstående undantag, kan du nu förenkla problemet till en logaritm. För att göra detta, använd formeln .
.
 .
. .
.Börja med att konvertera detta till en logaritm med formeln ovan:
 .
.
3. Beräkna detta för hand om möjligt. Kom ihåg: om  att lösa, tänker du på `
att lösa, tänker du på ` ` eller `Vilken exponent kan jag använda a höja till X att få?` Det är inte alltid möjligt att lösa detta utan en miniräknare, men om du har tur kommer du att få en lätt förenklad logaritm.
` eller `Vilken exponent kan jag använda a höja till X att få?` Det är inte alltid möjligt att lösa detta utan en miniräknare, men om du har tur kommer du att få en lätt förenklad logaritm.
 att lösa, tänker du på `
att lösa, tänker du på ` ` eller `Vilken exponent kan jag använda a höja till X att få?` Det är inte alltid möjligt att lösa detta utan en miniräknare, men om du har tur kommer du att få en lätt förenklad logaritm.
` eller `Vilken exponent kan jag använda a höja till X att få?` Det är inte alltid möjligt att lösa detta utan en miniräknare, men om du har tur kommer du att få en lätt förenklad logaritm. om
om  . Värdet av `?` är svaret på problemet. Du kanske måste prova några för att hitta den:
. Värdet av `?` är svaret på problemet. Du kanske måste prova några för att hitta den:


16 är vad du letade efter, så
 = 4.
= 4.
4. Lämna svaret i logaritmform om du inte kan förenkla det. Vissa logaritmer är mycket svåra att lösa för hand. Du behöver en miniräknare om du behöver svaret i ett praktiskt syfte. När du löser problem i mattelektionen förväntar sig din lärare förmodligen att du lämnar svaret som logaritm. Här är ett annat exempel som använder den här metoden för ett svårare problem:
 ?
? .(Observera att 3 försvinner i alla inledande loggar -- detta gäller alla baser).
.(Observera att 3 försvinner i alla inledande loggar -- detta gäller alla baser). och testa möjliga värden på ?:
och testa möjliga värden på ?:

Eftersom 58 hamnar mellan dessa två siffror har
 inget heltal som svar.
inget heltal som svar. .
.Metod 2 av 2: Arbeta med logaritmen för en kvot

1. Börja med ett divisionsproblem i en logaritm. Det här avsnittet hjälper dig att lösa problem med uttryck i formuläret  .
.
 .
. - Börja till exempel med det här problemet:
`Lös för n if.`

2. Kontrollera om det finns negativa siffror. Logaritmen för ett negativt tal är odefinierad. Om x eller y är ett negativt tal, kontrollera om problemet har en lösning innan du fortsätter:


3. Dela upp kvoten i två logaritmer. En användbar egenskap hos logaritmer beskrivs med formeln:  . Med andra ord, logaritmen för en kvot är alltid lika med täljarens logaritm, minus nämnarens logaritm.
. Med andra ord, logaritmen för en kvot är alltid lika med täljarens logaritm, minus nämnarens logaritm.
 . Med andra ord, logaritmen för en kvot är alltid lika med täljarens logaritm, minus nämnarens logaritm.
. Med andra ord, logaritmen för en kvot är alltid lika med täljarens logaritm, minus nämnarens logaritm.

→


4. Förenkla logaritmerna om möjligt. Om någon av de nya logaritmerna i uttrycket är ett heltal, förenkla dem nu.
 . Eftersom 3 = 27, förenkla
. Eftersom 3 = 27, förenkla  otäck 3.
otäck 3.

5. Isolera variabeln. Som alla matematiska problem hjälper det att isolera termen med variabeln på ena sidan av ekvationen. Eliminera liknande termer där det är möjligt för att förenkla ekvationen.


 .
.
6. Använd ytterligare egenskaper för logaritmer vid behov. För att isolera variabeln från andra termer inom samma logaritm, skriv om termen med olika logaritmiska egenskaper.
 .
.Runt n för att isolera, använd produktregeln för logaritmer:





7. Fortsätt att förenkla tills du hittar lösningen. Upprepa samma algebraiska och logaritmiska tekniker för att lösa problemet. Om det inte finns någon heltalslösning, använd en kalkylator och avrunda till närmaste signifikanta tal.


Sedan 3 = 19683, n =19683
"Dela logaritmer"
Оцените, пожалуйста статью