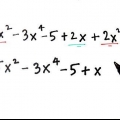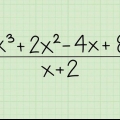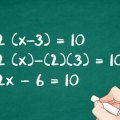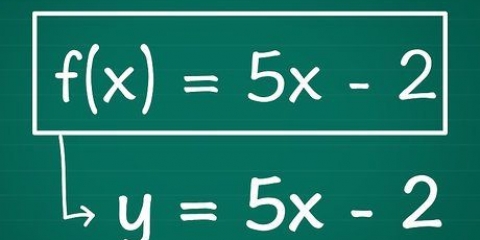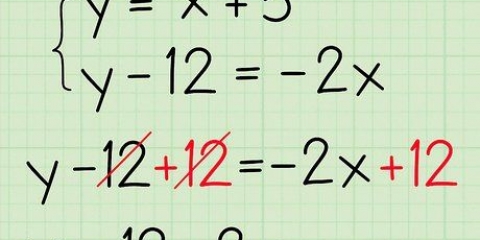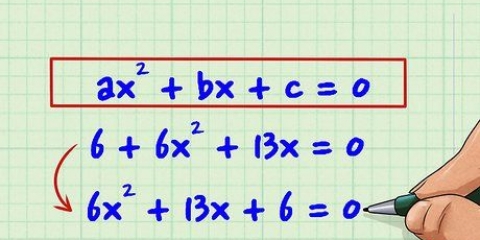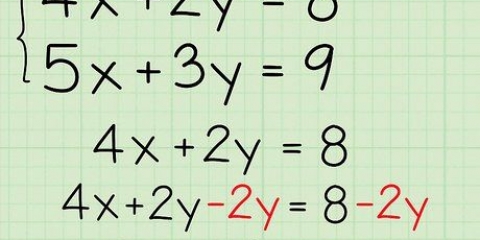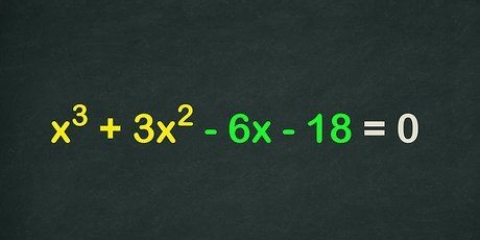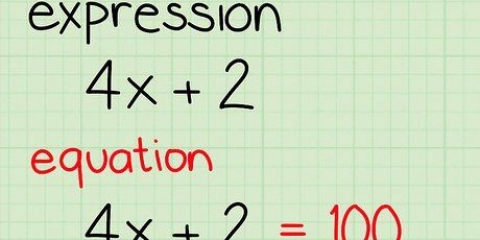Till exempel, 

Till exempel att  i
i  för att isolera, drar du
för att isolera, drar du  från båda sidor av ekvationen:
från båda sidor av ekvationen:




Till exempel att  att lösas i
att lösas i  , dividera varje sida av ekvationen med
, dividera varje sida av ekvationen med  :
:



Så lösningen på är är
är  .
. 

Till exempel, skriva om  så om
så om  .
. 
Till exempel,  .
. 
Till exempel för andragradspolynomet  , du måste hitta två siffror (
, du måste hitta två siffror ( och
och  ), Sann
), Sann  och
och  .
. För att du  du vet att ett av siffrorna kommer att vara negativt.
du vet att ett av siffrorna kommer att vara negativt. Det borde du se  och
och  . Så du splittrades
. Så du splittrades  på in
på in  och skriv om det andragradspolynomet:
och skriv om det andragradspolynomet:  .
. 
Till exempel de två första termerna i polynomet  är
är  . En term som förekommer i båda är
. En term som förekommer i båda är  . Detta blir den upplösta gruppen
. Detta blir den upplösta gruppen  .
. 
Till exempel de två andra termerna i polynomet  är
är  . En term som förekommer i båda är
. En term som förekommer i båda är  . Så är den upplösta gruppen
. Så är den upplösta gruppen  .
. 
Till exempel, efter faktorisering genom gruppering, blir  lika med
lika med  .
. Den första binomialen är  .
. Den andra binomialen är  .
. Så det ursprungliga andragradspolynomet,  kan skrivas som det faktoriserade uttrycket
kan skrivas som det faktoriserade uttrycket  .
. 
Till exempel att hitta den första lösningen på  , sätt det första binomialuttrycket lika med
, sätt det första binomialuttrycket lika med  och släppa dig
och släppa dig  på. Således:
på. Således:



Så, den första lösningen av det kvadratiska polynomet är
är  .
. 
Till exempel för att hitta den andra lösningen för  , sätt det andra binomialuttrycket lika med
, sätt det andra binomialuttrycket lika med  och släppa dig
och släppa dig  på. Således:
på. Således:



Så den andra lösningen av andragradspolynomet är lika med
lika med  .
.
Lös polynom
Ett polynom är ett uttryck som består av addition och subtraktion av termer. En term kan bestå av variabler, konstanter och koefficienter. När man löser polynom försöker man vanligtvis ta reda på vilka punkter x = 0. Lägsta gradspolynom har en eller två lösningar, beroende på om de är linjära polynom eller kvadratiska polynom. Dessa typer av polynom kan enkelt lösas med hjälp av elementär algebra och factoring. För att lösa högre grad av polynom kan du läsa artiklar på wikiHow.
Steg
Metod 1 av 2: Lösa ett linjärt polynom

1. Bestäm om du har att göra med ett linjärt polynom. Ett linjärt polynom är ett polynom av första graden. Detta betyder att ingen variabel kommer att ha en exponent (eller en exponent större än 1). Eftersom detta är ett förstagradspolynom har det exakt en lösning.
- Till exempel,
är ett linjärt polynom (eller polynom), eftersom variabeln
har ingen exponent (vilket är detsamma som en exponent för 1).

2. Gör ekvationen lika med noll. Detta är ett nödvändigt steg för att lösa alla polynom.


3. Flytta variabeltermen åt sidan. Gör detta genom att addera eller subtrahera konstanten från båda sidor av ekvationen. En konstant är en term utan variabel.
 i
i  för att isolera, drar du
för att isolera, drar du  från båda sidor av ekvationen:
från båda sidor av ekvationen:



4. Lös variabeln. Vanligtvis måste du dividera varje sida av ekvationen med konstanten. Detta ger dig lösningen av polynomet.
 att lösas i
att lösas i  , dividera varje sida av ekvationen med
, dividera varje sida av ekvationen med  :
:


Så lösningen på är
 är
är  .
.Metod 2 av 2: Lösa ett andragradspolynom

1. Bestäm om du har att göra med ett kvadratiskt polynom. Ett andragradspolynom är en andragradsekvation. Det betyder att ingen variabel har en exponent som är större än 2. Eftersom detta är ett andragradspolynom finns det två lösningar.
- Till exempel,
är ett kvadratiskt polynom, eftersom variabeln
a
har som exponent.

2. Se till att polynomet är skrivet i gradordning. Det betyder att termen med exponent  listas först följt av förstagradstermen, sedan konstanten.
listas först följt av förstagradstermen, sedan konstanten.
 listas först följt av förstagradstermen, sedan konstanten.
listas först följt av förstagradstermen, sedan konstanten. så om
så om  .
.
3. Gör ekvationen lika med noll. Detta är ett nödvändigt steg för att lösa alla polynom.
 .
.
4. Skriv om uttrycket som ett fyrtermsuttryck. Du gör detta genom att dividera förstagradstermen (de  termin). Du letar efter två tal vars summa är lika med förstagradskoefficienten och vars produkt är lika med konstanten.
termin). Du letar efter två tal vars summa är lika med förstagradskoefficienten och vars produkt är lika med konstanten.
 termin). Du letar efter två tal vars summa är lika med förstagradskoefficienten och vars produkt är lika med konstanten.
termin). Du letar efter två tal vars summa är lika med förstagradskoefficienten och vars produkt är lika med konstanten. , du måste hitta två siffror (
, du måste hitta två siffror ( och
och  ), Sann
), Sann  och
och  .
. du vet att ett av siffrorna kommer att vara negativt.
du vet att ett av siffrorna kommer att vara negativt. och
och  . Så du splittrades
. Så du splittrades  på in
på in  och skriv om det andragradspolynomet:
och skriv om det andragradspolynomet:  .
.
5. Faktor för gruppering. Det gör du genom att faktorisera en term som matchar de två första villkoren i polynomet.
 är
är  . En term som förekommer i båda är
. En term som förekommer i båda är  . Detta blir den upplösta gruppen
. Detta blir den upplösta gruppen  .
.
6. Faktorera den andra gruppen. Du gör detta genom att faktorisera en term som förekommer i polynomets andra två termer.
 är
är  . En term som förekommer i båda är
. En term som förekommer i båda är  . Så är den upplösta gruppen
. Så är den upplösta gruppen  .
.
7. Skriv om polynomet som två binomialer. Ett binomial är ett uttryck med två termer. Du har redan ett binomial, uttrycket inom parentes för varje grupp. Detta uttryck måste vara detsamma för alla grupper. Den andra binomialen görs genom att kombinera de två termerna som räknas in från varje grupp.
 lika med
lika med  .
. .
. .
. kan skrivas som det faktoriserade uttrycket
kan skrivas som det faktoriserade uttrycket  .
.
8. Hitta lösningen först. Det gör du genom att lösa  i den första binomialen.
i den första binomialen.
 i den första binomialen.
i den första binomialen. , sätt det första binomialuttrycket lika med
, sätt det första binomialuttrycket lika med  och släppa dig
och släppa dig  på. Således:
på. Således:


Så, den första lösningen av det kvadratiska polynomet
 är
är  .
.
9. Bestäm den andra lösningen. Du gör detta genom att  att lösa i den andra binomialen.
att lösa i den andra binomialen.
 att lösa i den andra binomialen.
att lösa i den andra binomialen. , sätt det andra binomialuttrycket lika med
, sätt det andra binomialuttrycket lika med  och släppa dig
och släppa dig  på. Således:
på. Således:


Så den andra lösningen av andragradspolynomet är
 lika med
lika med  .
.Tips
- Oroa dig inte för variabler, som t, eller om du har en ekvation som motsvarar f(x) istället för 0. Om frågan vill se rötter, nollor eller faktorer, behandla den som alla andra problem.
- Kom ihåg operationsordningen när du arbetar - rensa först parenteserna, gör sedan multiplikation och division, och slutligen addition och subtraktion.
Оцените, пожалуйста статью