Gungbrädans mitt=4 meter från nollpunkten. Barn 1=1 meter från nollpunkten Barn 2=5 meter från nollpunkten 



430 m*kg ÷ 130 kilo=3,31 m Tyngdpunkten är 3,31 meter från nollpunkten, eller mätt från nollpunkten är den 3,31 meter från änden av gungbrädans vänstra sida där nollpunkten placerades. 



Som vi löste det är nollan på vänster sida av gungbrädan. Vårt svar är 3,31 m, så vårt massacentrum är 3,31 m från nollan till vänster. Väljer du en ny nollpunkt, 1 m från vänster, får du som svar 2,31 m från massans centrum. Massans centrum är 2,31 m från den nya nollpunkten, dvs 1 m från vänster. Massans centrum är 2,31 + 1=3,31 m från vänster, och därför samma svar som vi beräknat tidigare. (Obs: När du mäter avstånd, kom ihåg att avstånd vänster från nollpunkten är negativa, och avstånd höger av det positivt.) 
I gungbrädaproblem är allt som spelar roll var tyngdpunkten är från vänster till höger längs gungbrädans linje. Senare kan du lära dig mer avancerade sätt att beräkna tyngdpunkten i två dimensioner.
Beräkna tyngdpunkten
Tyngdpunkten (massacentrum) är centrum för ett objekts viktfördelning - punkten där tyngdkraften verkar på objektet. Detta är den punkt där objektet är i perfekt balans, oavsett hur objektet vrids eller roteras runt den punkten. Om du vill veta hur man beräknar ett föremåls tyngdpunkt behöver du vikten av föremålet och alla föremål på det. Sedan bestämmer du en nolla och bearbetar de kända storheterna i ekvationen, för att beräkna tyngdpunkten för ett objekt eller system. Om du vill veta hur man beräknar tyngdpunkten, följ stegen nedan.
Steg
Metod 1 av 4: Bestäm vikten

1. Beräkna vikten på föremålet. När du beräknar tyngdpunkten måste du först ta reda på föremålets vikt. Låt oss säga att du vill beräkna vikten av en gungbräda med en massa på 30 kilo. Eftersom det är ett symmetriskt föremål kommer dess tyngdpunkt att vara exakt i mitten (om ingen sitter på det). Men om det finns människor med olika massa på gungbrädan, så blir problemet lite mer komplicerat.

2. Beräkna de extra vikterna. För att bestämma tyngdpunkten för gungbrädan med två barn på den, måste du bestämma den individuella vikten för varje barn. Det första barnet väger 40 kilo och det andra barnet väger 60 kilo.
Metod 2 av 4: Bestäm nollpunkten

1. Välj en nollpunkt. Nollpunkten är vilken startpunkt som helst på ena sidan av gungbrädan. Du kan placera nollan på ena sidan av gungbrädan eller på andra sidan. Låt oss säga att gungbrädan är 6 meter lång. Låt oss sätta nollan på vänster sida av gungbrädan, nära det första barnet.

2. Mät avståndet från nollpunkten till mitten av huvudobjektet samt till de två extra vikterna. Låt oss säga att barnen är vardera 1 meter från varje ände av gungbrädan. Gungbrädans mitt är gungbrädans mitt, eller 3 meter, eftersom 6 meter dividerat med 2 är lika med 3. Här är avstånden från mitten av det största föremålet och de två extra vikterna bildar nollpunkten:
Metod 3 av 4: Bestäm tyngdpunkten

1. Multiplicera avståndet för varje objekt till nollpunkten med dess vikt för att hitta ögonblicket. Detta ger dig ögonblicket för varje objekt. Så här multiplicerar du avståndet för varje objekt från nollpunkten med dess vikt:
- Gungbrädan: 30 kilo x 3 m=90 m*kg.
- Barn 1=40 kilo x 1 m=40 m*kg.
- Barn 2=60 kilo x 5 m=300 m*kg.

2. Lägg ihop de tre ögonblicken. Räkna bara ut följande: 90 m*kg + 40 m*kg + 300 m*kg=430 m*kg. Det totala momentet är 430 m*kg.

3. Lägg ihop vikterna av alla föremål. Hitta summan av vikterna för gungbrädan och de två barnen. Gör så här: 30 kilo + 40 kilo + 60 kilo = 130 kilo.

4. Dela det totala momentet med den totala vikten. Får avståndet från nollpunkten till objektets tyngdpunkt. Detta genom att dividera 430 m * kg med 130 kilo.
Metod 4 av 4: Kontrollera ditt svar

1. Hitta tyngdpunkten i diagrammet. Om tyngdpunkten du har hittat ligger utanför objektsystemet, då har du hittat fel svar. Kanske har du räknat ut avståndet från mer än en punkt. Försök igen med bara en nollpunkt.
- Till exempel, för personer som sitter på gungbrädan, bör tyngdpunkten vara någonstans på gungbrädan, inte till vänster eller höger om gungbrädan. Det behöver inte vara på en person.
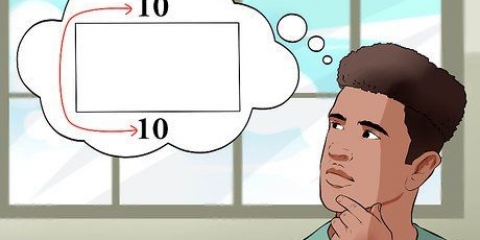
- Detta gäller även problem i två dimensioner. Rita en fyrkant precis stor nog att passa alla objekt i ditt problem. Tyngdpunkten måste vara inom denna ruta.

2. Kontrollera dina beräkningar om ditt svar är för litet. Om du väljer ena änden av systemet som din nolla, placerar ett litet svar tyngdpunkten bredvid ena änden. Detta kan vara det rätta svaret, men det är ofta en indikation på att något har gått fel. Har ni vikten och avståndet med varandra i beräkningen multiplicerat? Det är rätt sätt att hitta det här ögonblicket. Om du av misstag läggas ihop, då får du nog ett mycket mindre svar.

3. Kontrollera din beräkning om du har hittat mer än en tyngdpunkt. Varje system har bara en enda tyngdpunkt. Om det finns fler kan du ha hoppat över steget där du var tvungen att lägga ihop alla ögonblick. Tyngdpunkten är den total moment dividerat med total vikt. Du behöver inte varje ögonblick att dela med sig av varje vikt, vilket bara ger dig positionen för varje objekt.

4. Markera nollan om ditt svar är ett heltal av. Svaret i vårt exempel är 3,31 m Antag att du fick 2,31 m, 4,31 m eller något annat tal som slutar på `.31.Det beror förmodligen på att vi valde den vänstra änden av gungbrädan som nolla, medan du valde den högra änden eller en annan punkt ett heltalsavstånd från vår nolla. Ditt svar är korrekt, oavsett vilken nolla du väljer! Du behöver bara komma ihåg det nollan står alltid för x=0. Här är ett exempel:

5. Se till att alla dina mått är raka linjer. Anta att du ser ett annat exempel med "barn på gungbräda", men det ena barnet är mycket större än det andra, eller så hänger en pojke under gungbrädan istället för att sitta på den. Ignorera skillnaden och ta alla dina mått längs gungbrädans raka linje. Att mäta avstånd i en vinkel kommer att ge svar som är nära, men något annorlunda.
Tips
- För att bestämma avståndet en person måste röra sig för att balansera gungbrädan på stödet, använd denna formel: (flyttar vikt) / (totalvikt)=(avstånd över vilken tyngdpunkten har rört sig) / (sträcka över vilken vikten har flyttats). Denna formel kan skrivas om för att visa att avståndet som vikten (personen) måste förflyttas är lika med avståndet mellan tyngdpunkten och stödpunkten, gånger personens vikt dividerat med totalvikten. Det måste det första barnet också -1,31 m *40 kilo / 130 kilo=-0.flytta 40 m (till slutet av gungbrädan). Eller borde det andra barnet -1.08 m *130 kilo / 60 kilo=-2.flytta 84 m. (till mitten av gungbrädan).
- För att hitta tyngdpunkten för ett tvådimensionellt objekt, använd formeln Xcg=∑xW/∑W för att hitta tyngdpunkten längs x-axeln och Ycg=∑yW/∑W för att hitta tyngdpunkten längs y-axeln. Den punkt där de skär varandra är tyngdpunkten.
- Definitionen av tyngdpunkten för en allmän massfördelning är (∫ r dW/∫ dW) där dW är lika med derivatan av vikten, r är positionsvektorn och där integralerna ska tolkas som Stieltjes-integraler över helheten kropp. De kan dock uttryckas som mer konventionella Riemann- eller Lebesgue-volymintegraler för distributioner med en sannolikhetstäthetsfunktion. Från och med denna definition kan alla egenskaper hos tyngdpunkten, inklusive de som används i denna artikel, härledas från egenskaperna hos Stieltjes-integraler.
Varningar
- Försök inte blint att tillämpa dessa mekaniker utan att förstå teorin, vilket kan leda till fel. Försök först förstå de bakomliggande lagarna/teorierna.
"Beräkna tyngdpunkten"
Оцените, пожалуйста статью