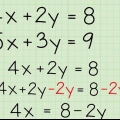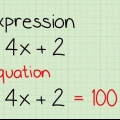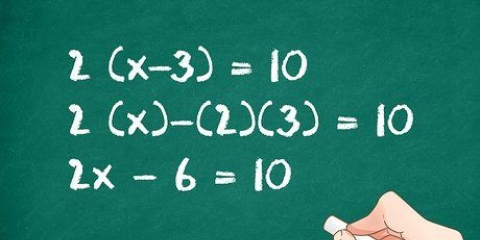2x - 2x = 0 4y - 2y = 2y 8 - 2 = 6 2x + 4y = 8-(2x + 2y = 2)=0 +2y = 6 
2y = 6 Dividera 2y och 6 med 2 och få y = 3 
Infoga y = 3 i ekvationen 2x + 2y = 2 och lös x. 2x + 2(3) = 2 2x + 6 = 2 2x = -4 x = - 2 Du har löst ekvationssystemet genom subtraktion. (x, y) = (-2, 3) 
Fyll i (-2, 3) för (x, y) i ekvationen 2x + 4y = 8. 2(-2) + 4(3) = 8 -4 + 12 = 8 8 = 8 Fyll i (-2, 3) för (x, y) i ekvationen 2x + 2y = 2. 2(-2) + 2(3) = 2 -4 + 6 = 2 2 = 2 

3x + x = 4x 6y + -6y = 0 8 + 4 = 12 Om du kombinerar detta får du en ny produkt: 3x + 6y = 8 +(x - 6y = 4) = 4x + 0 = 12 
4x + 0 = 12 4x = 12 Dividera 4x och 12 med 3 för att få x = 3 
Koppla in x = 3 i ekvationen x - 6y = 4 för att hitta y. 3 - 6 år = 4 -6y = 1 Dela -6y och 1 med -6 för att få y = -1/6. Du har löst ekvationssystemet med addition. (x, y) = (3, -1/6) 
Fyll i (3, -1/6) för (x, y) i ekvationen 3x + 6y = 8. 3(3) + 6(-1/6) = 8 9 - 1 = 8 8 = 8 Fyll i (3, -1/6) för (x, y) i ekvationen x - 6y = 4. 3 - (6 * -1/6) =4 3 - - 1 = 4 3 + 1 = 4 4 = 4 

2 (2x - y = 2) 4x - 2y = 4 
3x + 2y = 10 + 4x - 2y = 4 7x + 0 = 14 7x = 14 

x = 2 ---> 2x - y = 2 4 - y = 2 -y = -2 y = 2 Du har löst ekvationssystemet med multiplikation. (x, y) = (2, 2) 
Fyll i (2, 2) för (x, y) i ekvationen 3x + 2y = 10. 3(2) + 2(2) = 10 6 + 4 = 10 10 = 10 Fyll i (2, 2) för (x, y) i ekvationen 2x - y = 2. 2(2) - 2 = 2 4 - 2 = 2 2 = 2 

x = 2 - 4y --> 2x + 3y = 9 2(2 - 4y) + 3y = 9 4 - 8y + 3y = 9 4 - 5 år = 9 -5y = 9 - 4 -5y = 5 -y = 1 y = - 1 
y = -1 --> x = 2 - 4y x = 2 - 4(-1) x = 2 - -4 x = 2 + 4 x = 6 Du löste ekvationssystemet med hjälp av substitution. (x, y) = (6, -1) 
Fyll i (6, -1) för (x, y) i ekvationen 2x + 3y = 9. 2(6) + 3(-1) = 9 12 - 3 = 9 9 = 9 Fyll i (6, -1) för (x, y) i ekvationen x + 4y = 2. 6 + 4(-1) = 2 6 - 4 = 2 2 = 2
Lösa ett ekvationssystem
Att lösa ett ekvationssystem kräver att man hittar värdet av flera variabler i flera ekvationer. Du kan lösa ett ekvationssystem med hjälp av addition, subtraktion, multiplikation eller substitution. Om du vill lära dig hur man löser ett ekvationssystem behöver du bara följa dessa steg.
Steg
Metod 1 av 4: Lös genom subtraktion

1. Skriv den ena ekvationen över den andra. Att lösa dessa ekvationer med subtraktion är en idealisk metod om du ser att båda ekvationerna har samma variabel med samma koefficient och tecken. Till exempel, om båda ekvationerna har variabeln -2x, kan du använda subtraktion för att hitta värdet på båda variablerna.
- Skriv en ekvation ovanför den andra så att variablerna x och y i båda ekvationerna och talen ligger under varandra. Placera minustecknet bredvid det nedre numret.
- Till exempel: Om du har följande två ekvationer: 2x + 4y = 8 och 2x + 2y = 2, skulle det se ut så här:
- 2x + 4y = 8
- -(2x + 2y = 2)

2. Subtrahera liknande termer. Nu när de två ekvationerna är justerade, är allt du behöver göra att subtrahera liknande termer. Gör detta med en term i taget:

3. Lös för den återstående terminen. Ta bort eventuella nollor från ekvationen som har skapats, den ändrar inte värdet och lös den återstående ekvationen.

4. Ange det hittade värdet för variabeln i en av ekvationerna. Nu när du vet att y = 3 kan du koppla in detta värde till den ursprungliga ekvationen för att lösa x. Oavsett vilken ekvation du väljer är svaret detsamma. Så använd den enklaste ekvationen!

5. Kontrollera ditt svar. För att vara säker på att ditt svar är korrekt, skriv in båda svaren i båda ekvationerna. Så här gör du det:
Metod 2 av 4: Lös genom tillägg

1. Skriv den ena ekvationen över den andra. Att lösa ett ekvationssystem genom addition är den bästa metoden, om du märker att båda ekvationerna har en variabel med samma koefficient, men med olika tecken; till exempel, om en ekvation innehåller variabeln 3x och den andra variabeln -3x.
- Skriv en ekvation ovanför den andra så att variablerna x och y i båda ekvationerna och talen ligger under varandra. Placera plustecknet bredvid det nedre numret.
- T.ex.: Du har följande två ekvationer 3x + 6y = 8 och x - 6y = 4, skriv sedan den första ekvationen ovanför den andra som visas nedan:
- 3x + 6y = 8
- +(x - 6y = 4)

2. Lägg till liknande termer tillsammans. Nu när de två ekvationerna är inriktade ovanför varandra behöver du bara lägga till termerna med samma variabel:

3. Lös för den återstående terminen. Ta bort eventuella nollor från ekvationen som har uppstått, det ändrar inte värdet. Lös den återstående ekvationen.

4. Ange det funna värdet för denna variabel i en av ekvationerna. Nu när du vet att x = 3 kan du koppla in detta värde till den ursprungliga ekvationen för att lösa y. Oavsett vilken ekvation du väljer är svaret detsamma. Så använd den enklaste ekvationen!

5. Kontrollera ditt svar. För att vara säker på att ditt svar är korrekt, skriv in båda svaren i båda ekvationerna. Så här gör du det:
Metod 3 av 4: Lös genom multiplikation

1. Skriv den ena ekvationen över den andra. Skriv en ekvation ovanför den andra så att variablerna x och y i båda ekvationerna och talen ligger under varandra. Om du använder multiplikation gör du det eftersom ingen av variablerna har lika koefficienter - just nu.
- 3x + 2y = 10
- 2x - y = 2

2. Säkerställ lika koefficienter. Multiplicera sedan en eller båda ekvationerna med ett tal, så att en av variablerna har samma koefficient. I det här fallet kan du multiplicera hela den andra ekvationen med 2 så att -y är lika med -2y och därmed den första y-koefficienten. Så här gör du det:

3. Addera eller subtrahera ekvationerna. Nu behöver du bara eliminera lika termer genom att lägga till eller subtrahera. Eftersom du har att göra med 2y och -2y här, är det vettigt att använda additionsmetoden eftersom den är lika med 0. Om du har att göra med 2y + 2y, använd subtraktionsmetoden. Här är ett exempel på hur man använder additionsmetoden för att eliminera variabler:

4. Lös detta för den återstående terminen. Detta löses enkelt genom att hitta värdet på termen som du ännu inte har eliminerat. Om 7x = 14, då är x = 2.

5. Ange det hittade värdet i en av ekvationerna. Skriv in termen i en av de ursprungliga ekvationerna för att lösa den andra termen. Välj den enklaste ekvationen för detta, detta är den snabbaste.

6. Kontrollera ditt svar. För att vara säker på att ditt svar är korrekt, skriv in båda svaren i båda ekvationerna. Så här gör du det:
Metod 4 av 4: Lös genom substitution

1. Isolera en variabel. Substitution är idealisk när en av koefficienterna i en av ekvationerna är lika med 1. Sedan är allt du behöver göra att isolera denna variabel på ena sidan av ekvationen för att hitta dess värde.
- Om du arbetar med ekvationerna 2x + 3y = 9 och x + 4y = 2, måste du isolera x i den andra ekvationen.
- x + 4y = 2
- x = 2 - 4y

2. Fyll i värdet på variabeln du isolerade i den andra ekvationen. Ta värdet på den isolerade variabeln och koppla in den i den andra ekvationen. Naturligtvis inte i samma ekvation annars löser du ingenting. Här är ett exempel på hur man gör det:

3. Lös för den återstående variabeln. Nu när du vet att y = - 1, koppla in detta värde till den enklare ekvationen för att hitta värdet på x. Här är ett exempel på hur du gör det:

4. Kontrollera ditt svar. För att vara säker på att ditt svar är korrekt, skriv in båda svaren i båda ekvationerna. Så här gör du det:
Tips
- Du bör nu kunna lösa vilket linjärt ekvationssystem som helst med hjälp av addition, subtraktion, multiplikation eller substitution, men en metod är vanligtvis den mest lämpliga beroende på ekvationerna.
"Lösa ett ekvationssystem"
Оцените, пожалуйста статью