För små former kan du använda centimeter, medan meter eller kilometer är mer lämpliga för större omkretsar. När de motsatta sidorna av rektanglar är lika behöver du bara mäta en av de motsatta sidorna. 
Fortsätt med exemplet: föreställ dig att förutom en längd på 3 cm är bredden på din rektangel 5 cm. 

Så i det här exemplet beräknar du 3 + 3 + 5 + 5 = 16 (omkretsen). Du kan också använda formeln 2 x (längd + bredd) för rektanglar, eftersom längden och bredden på de motsatta sidorna är lika och därmed fördubblas. Så i vårt exempel är detta: 2 x 8 = 16. 
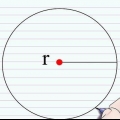
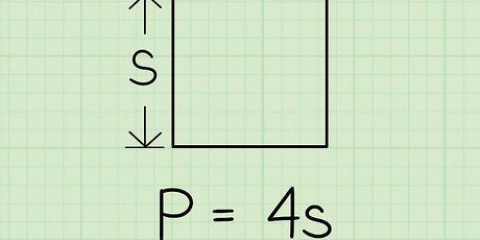
Fyrkant: längd på varje sida x 4 Triangel: lägg ihop alla sidor Oregelbunden polygon: lägg ihop alla sidor Cirkel: 2 x π x radie eller π x diameter. π-symbolen står för Pi (uttalas paj). Om du har en π-knapp på din räknare kan du använda den för att vara mer exakt när du använder den här formeln. Om inte kan du avrunda värdet på π till 3,14. Termen "radie" avser avståndet mellan centrum av en cirkel och dess yttre gräns (omkrets), medan "diameter" avser längden av en tänkt linje mellan två motsatta punkter på omkretsen av en cirkel som går genom centrum av en cirkel. cirkeln, cirkeln går. 

Du kan dela upp formen i vertikala och horisontella segment av en enhet (cm, m) om du vill visualisera hur ytmåttet kommer att se ut. 
Du kan skriva "kvadratenheter/enheter i kvadrat" som: cm² m² km² 
Parallelogram: bas x höjd Fyrkant: sida 1 x sida 2 Triangel: ½ x bas x höjd. Vissa matematiker använder notationen: A=½bh. Cirkel: π x r² (där r = radie) Termen "radie" syftar på avståndet mellan centrum av en cirkel och dess yttre gräns (omkrets), och de små två i upphöjd (kvadraten) indikerar att värdet de två tillhör multipliceras med sig själv.
Bestäm area och omkrets
Omkretsen är längden på hela den yttre gränsen för en plan (tvådimensionell) figur, och arean är måttet på dess storlek. Yta och omkrets är extremt användbara mått som kan användas i hushållsprojekt, konstruktion, gör-det-själv-projekt och när du uppskattar mängden material du kan behöva. Om du till exempel vill måla ett rum måste du veta hur mycket färg du behöver eller med andra ord hur mycket yta färgen kan täcka. Detsamma kan sägas när man gör i ordning en trädgård, bygger ett staket eller gör olika andra sysslor hemma. I dessa situationer kan du använda yta och omkrets för att spara tid och pengar när du köper material.
Steg
Del 1 av 2: Bestämma omkrets

1. Bestäm formen du vill mäta. Omkretsen är den yttre gränsen runt en sluten geometrisk figur, och olika former kräver olika tillvägagångssätt. Om formen vars omkrets du vill hitta inte är en sluten form, kan omkretsen inte bestämmas.
- Om det är första gången du beräknar omkretsen, prova en rektangel eller en kvadrat. Dessa regelbundna former gör det lättare att bestämma omkretsen.

2. Rita en rektangel på ett papper. Du använder den här rektangeln som en övningsform och bestämmer dess omkrets. Se till att de motsatta sidorna av din rektangel är lika långa.

3. Bestäm längden på ena sidan av din rektangel. Det kan du göra med linjal, måttband eller genom att hitta på ett eget exempel. Skriv denna siffra bredvid sidan den representerar, så att du inte glömmer längden. Anta att längden på ena sidan av din rektangel är 3 cm.

4. Bestäm bredden på ena sidan av din rektangel. Du kan mäta bredden med linjal, måttband eller genom att göra ett eget exempel. Skriv värdet för din bredd bredvid den horisontella sidan av din rektangel som den representerar.

5. Skriv de korrekta måtten på motsatta sidor av din rektangel. Rektanglar har fyra sidor, men längden på de motsatta sidorna kommer att vara densamma. Detta gäller även bredden på din rektangel. Skriv längden och bredden som används i exemplet (3 respektive 5 cm) på motsatta sidor av din rektangel.

6. Lägg ihop alla sidor. Under exemplet du gjorde eller skrev ner, skriv följande: längd + längd + bredd + bredd.

7. Justera ditt tillvägagångssätt för olika former. Tyvärr kommer olika former att kräva olika formler för omkretsen. I verkliga exempel kan du mäta den yttre gränsen för valfri sluten geometrisk form för att bestämma dess omkrets. Men du kan också använda följande formler för att hitta omkretsen av andra vanliga former:
Del 2 av 2: Fastställande av område

1. Bestäm dimensionerna på din form. Rita en rektangel eller använd samma rektangel som du ritade när du bestämmer omkretsen. I det här exemplet beräknar du arean av en rektangel med hjälp av dess höjd och bredd.
- Du kan arbeta med linjal eller måttband, eller komma med ett eget exempel. I det här exemplet är längden och bredden lika med föregående exempel som användes för att hitta omkretsen: 3 respektive 5 .

2. Förstå den sanna innebörden av ytan. Att bestämma arean inom en omkrets är som att dela det tomma utrymmet i din form i 1 gånger 1. rutor. Ytan kan vara mindre eller större än omkretsen, beroende på formen.

3. Multiplicera längden på din rektangel med bredden. I exemplet: area = 3 x 5, vilket är 15 kvadratmeter. Måttenheten för området ska alltid skrivas i kvadratenheter (kvadratkilometer, kvadratmeter etc.).).

4. Ändra din formel beroende på formen. Olika geometriska former kommer tyvärr att kräva ett annat tillvägagångssätt för att beräkna arean. Du kan använda följande formler för att hitta arean av några vanliga former:
Tips
- Dessa area- och omkretsformler fungerar bara för arean (volymen) av en platt form. Om du behöver hitta innehållet i en tredimensionell form (volymen) måste du leta efter formler för volym, till exempel för koner, kuber, cylindrar, prismor och pyramider.
Förnödenheter
- Papper
- Penna
- Miniräknare (valfritt)
- Måttband (valfritt)
- Linjal (valfritt)
Оцените, пожалуйста статью