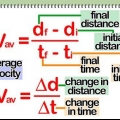
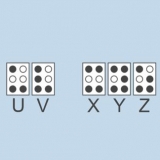
Förskjutning = d Förskjutning är den sträcka som ett givet föremål har tillryggalagt. Vanligtvis noteras enheten för förskjutning i meter. Tid = t Hastighet = v Vektoriell hastighet är hastigheten för ett föremål i en viss riktning. När vi beräknar momentan hastighet letar vi efter ett objekts hastighet vid ett givet ögonblick t (tid). Hastigheten noteras vanligtvis i meter per sekund (m/s). Lutning (eller "backe") = m Här kan det vara användbart att visa ett objekts rörelse i en enkel x-y-graf med tiden plottad längs x-axeln och förskjutning längs y-axeln. Då är linjens lutning vid en viss punkt objektets hastighet. 
Hastigheten (v) vid en given tidpunkt (t) är lika med lutningen (förändringshastigheten) för ovanstående ekvation, där förskjutningen (d) plottas mot tiden (t). 
En allmän regel för att hitta derivatan: Om y = a*x, så är derivatan a*n*x. Denna regel tillämpas på vilken term som helst i polynomet. Konstanten (talet utan en variabel bredvid) kommer att försvinna eftersom den multipliceras med 0. 






För att beräkna momentan hastighet är det nödvändigt att beräkna lutningen på en graf för en given punkt. 




Värdet till vilket lutningen rör sig när H närmar sig 0 är gränsen. Detta är lika med lutningen av tangenten till kurvan. Tangenten är en rät linje definierad som en parallell till parabeln över ett oändligt kort avstånd. Tangentlinjens lutning är därför parabelns/kurvans lutning om H blir ett oändligt litet avstånd på linjen. Ekvationen för att hitta tangenten är derivatan av ekvationen för förskjutningsfunktionen, som i del ett. 
Beräkna momentan hastighet
Vektoriell hastighet (hastighet på engelska) definieras som hastigheten för ett objekt i en viss riktning. För allmänna ändamål är det så enkelt att hitta ett föremåls hastighet som att dividera den tillryggalagda sträckan med den tid det tar att resa den sträckan. Men detta ger bara medelhastigheten längs en given bana. Med hjälp av matematiska ekvationer och derivator är det möjligt att beräkna objektets hastighet vid varje given tidpunkt längs vägen. Det här kallas momentan hastighet. För bekvämlighetens och läsbarhetens skull kommer vi att hänvisa till hastighet i det följande, både när vi menar "normal" hastighet och vektoriell hastighet.
Steg
Metod 1 av 2: Beräkna den momentana hastigheten

1. Vad är "momentan hastighet". Objekt som rör sig kan göra det med en konstant hastighet – som rör sig med konstant hastighet under hela resan. En löpare som joggar längs en fotbollsplan håller ungefär samma hastighet över hela planens längd. Objekt kan också röra sig med en varierande hastighet. Till exempel kommer en bil som kör längs en väg med många kurvor inte att ha samma hastighet hela tiden – i kurvorna minskar hastigheten för att sedan öka igen på raksträckorna.
- Omedelbar hastighet är ett mått på ett föremåls hastighet vid vilken tidpunkt som helst. Till exempel är den momentana hastigheten för en raket exakt en sekund efter antändning av drivmedlet mycket lägre än dess momentana hastighet 30 sekunder efter start, om raketen har hunnit få fart.

2. Känn till dina variabler. När du har att göra med momentana hastighetsberäkningar kommer du nästan alltid att stöta på vissa variabler någon gång. Dessa variabler är:

3. Ett exempel. Låt oss säga att förskjutningen av ett föremål kan representeras av en ekvation: förskjutning(er) = 3t + 4t + 7. Grafen för denna funktion är en krökt linje eller parabel, där x-axeln representerar tid och y-axeln representerar förskjutning.

4. För att beräkna den momentana hastigheten för ett föremål med en förskjutning enligt ovanstående funktion behöver vi derivatan av denna funktion. En funktions derivata är lika med lutningen för funktionen vid vilken punkt som helst på grafen. För att hitta derivatan differentierar vi funktionen enligt denna formel:

5. Använd den här formeln för att beräkna derivatan av funktionen. Om vi skriver detta som y = 3x + 4x + 7, så är derivatan (3*2)*x+(4*1)*x+(7*0)*x

6. Förenkla ekvationen. Att multiplicera alla termer inom parentes ger 6x+ 4x+ 0x

7. Fortsätt att förenkla. Denna ekvation kan skrivas som 6x + 4. De "0x" termen blir då lika med 0, medan den "4x" termen förenklas till 4 (n = 1.)

8. Gör denna nya funktion lika med lutningen m. Vi använder denna derivata funktion för att hitta lutningen av den ursprungliga ekvationen y = 3x + 4x + 7 för ett givet värde på x (tid). Den ursprungliga lutningen av ekvationen vid varje given tidpunkt är den momentana hastigheten.

9. Hitta objektets momentana hastighet under t=4 sekunder. Allt du behöver göra är att ange tidsvärdet i variabeln x för ekvationens derivata. Detta ger följande ekvation y = 6(4) + 4 . Detta är förenklat till 28. Objektets momentana hastighet under t=4 sekunder är 28 m/s.
Metod 2 av 2: Förstå en derivata

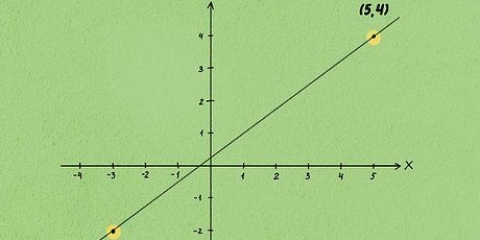
1. Rita ett vanligt x-y koordinatsystem. För att korrekt förstå hur en derivata kan hjälpa till att hitta ett objekts momentana hastighet, är en grafisk representation mycket användbar. Y-axeln representerar objektets förskjutning, medan x-axeln representerar tid.
- Grafen kan fortsätta under x-axeln. Om linjen som representerar objektets rörelse faller under x-axeln betyder det att objektet rör sig i motsatt riktning och före startpunkten. Vanligtvis kommer grafen inte att sträcka sig utanför y-axeln. Hastighet mäts inte för objekt som rör sig bakåt i tiden!
- Om du inte är säker på hur man ritar en graf eller exakt vad x-axeln och y-axeln representerar, lär dig hur du kan rita en graf över en funktion.

2. Rita en krökt linje, med början från punkten på linjen x=0, i x-axelns riktning. Linjens lutning är den hastighet med vilken y ändras dividerat med den hastighet med vilken x ändras. Så, om y är lika med förskjutning och x är lika med tid, så är lutning lika med hastighet.

3. För att hitta lutningen på en linje för en viss punkt använder vi ett trick där vi hittar gränsen för ekvationen. För att hitta gränsen krävs två punkter P och Q på en krökt linje och att hitta lutningen på linjen genom båda punkterna när avståndet mellan de två punkterna blir mindre och mindre.

4. Välj en punkt P på linjen. Placera till exempel P på x=1. Den exakta platsen spelar ingen roll. Välj ett värde som är bekvämt.

5. Välj en andra punkt Q på linjen. Q bör vara ett kort avstånd från P. I vårt exempel är Q i punkten med x=3, medan P är i punkten med x=1.

6. Hitta lutningen mellan P och Q. Lutningen mellan P och Q blir då (skillnaden i y-värde för P och Q)/(skillnaden i x-värde P och Q). Vi hänvisar till denna skillnad i x-värden för P och Q som H. I detta fall är H lika med 3-1=2.

7. Gör värdet på H mindre. Med andra ord, för Q närmare P på x-axeln och beräkna sedan lutningen igen mellan P och Q. Gör detta upprepade gånger, varje gång minska avståndet mellan P och Q. Efter att ha beräknat detta några gånger bör det stå klart att lutningen närmar sig ett visst värde. Så länge H>0 kommer lutningen aldrig att nå detta värde, utan bara närma sig. Vi säger då att lutningen gränsen närmar sig.

8. Använd derivator för att hitta lutningen om H representerar ett oändligt litet intervall på linjen. Derivatan av en ekvation hittas av "x, är N*x" att tillämpa på vilken term som helst i den ursprungliga ekvationen.
Tips
- Förskjutning är som avstånd, men i en viss riktning, så förskjutning är en vektor och hastighet är en skalär storhet. Förskjutning kan vara negativ medan avstånd bara kan vara positivt.
- För att hitta accelerationen (hastighetsförändringen över tid), använd metoden i del ett för att hitta derivatan av din förskjutningsfunktion. Ta sedan derivatan av det. Detta ger dig sedan ekvationen för att hitta accelerationen vid en given tidpunkt - allt du behöver göra är att ange tidsvärdet i denna andraderivata.
- Ekvationen som relaterar y (förskjutning) till x (tid) kan vara mycket enkel, som t.ex. y= 6x + 3. I detta fall är lutningen konstant och det är inte nödvändigt att hitta en derivata av lutningen. Det är lika med 6, enligt den linjära ekvationen y = mx + b.
"Beräkna momentan hastighet"
Оцените, пожалуйста статью