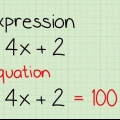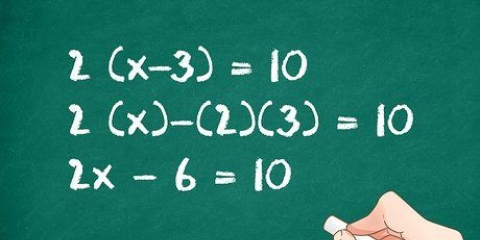4x = 8 - 2y (4x)/4 = (8/4) - (2y/4) x = 2 - y 
Du vet nu att: x = 2 - y. Den andra ekvationen, som du inte har ändrat ännu, är: 5x + 3x = 9. I den andra ekvationen, ersätt x med `2 - ½y`: 5(2 - ½y) + 3y = 9. 
5(2 - ½y) + 3y = 9 10 – (5/2)y + 3y = 9 10 – (5/2)y + (6/2)y = 9 (Om du inte förstår det här steget, lär dig hur man lägger till bråk. Detta är ofta, men inte alltid, nödvändigt med denna metod). 10 + y = 9 y = -1 y = -2 
Du vet nu att: y = -2 En av de ursprungliga ekvationerna är: 4x + 2y = 8. (Båda ekvationerna kan användas för detta steg). Koppla in -2 istället för y: 4x + 2(-2) = 8. 4x - 4 = 8 4x = 12 x = 3 
Om du slutar med en ekvation utan variabler och som inte är sann (till exempel 3 = 5), så har problemet ingen lösning. (Om du har ritat ut ekvationerna kommer du att se att de är parallella och aldrig skär varandra). Om du slutar med en ekvation utan variabler, men de väl är sant (till exempel 3 = 3), så har problemet ett oändligt antal lösningar. De två ekvationerna är exakt lika med varandra. (Om du ritar de två ekvationerna kommer du att se att de överlappar varandra exakt). 

Anta att du har ekvationssystemet 3x - y = 3 och -x + 2y = 4. Låt oss modifiera den första ekvationen så att variabeln y håller på att elimineras. (Du kan också göra detta för X gör och få samma svar). De - y` av den första ekvationen bör elimineras med+ 2 år ` i den andra ekvationen. Vi kan göra detta genom att - y att multiplicera med 2. Vi multiplicerar båda sidor av den första ekvationen med 2, enligt följande: 2(3x - y)=2(3), och sålunda 6x - 2y = 6. Nu ska - 2 år falla bort mot +2 år i den andra ekvationen. 
Dina ekvationer är: 6x - 2y = 6 och -x + 2y = 4. Kombinera vänster sidor: 6x - 2y - x + 2y = ? Kombinera de högra sidorna: 6x - 2y - x + 2y = 6 + 4. 
Du har: 6x - 2y - x + 2y = 6 + 4. Gruppera variablerna X och y med varandra: 6x - x - 2y + 2y = 6 + 4. Förenkla: 5x = 10 Lös för x: (5x)/5 = 10/5, så att x = 2. 
Du vet det x = 2, och den där av dina ursprungliga ekvationer 3x - y = 3 är. Koppla in 2 istället för x: 3(2) - y = 3. Lös för y i ekvationen: 6 - y = 3 6 - y + y = 3 + y, så 6 = 3 + y 3 = y 
Om din kombinerade ekvation inte har några variabler och inte är sann (som 2 = 7), så finns det ingen lösning vilket gäller för båda ekvationerna. (Om du ritar båda ekvationerna ser du att de är parallella och aldrig skär varandra). Om din kombinerade ekvation inte har några variabler och är sann (som 0 = 0), så finns det ett oändligt antal lösningar. De två ekvationerna är faktiskt identiska. (Om du sätter dessa på en graf ser du att de helt överlappar varandra). 

Den första ekvationen är: 2x + y = 5. Ändra detta till: y = -2x + 5. Den andra ekvationen är: -3x + 6y = 0. Ändra detta till 6y = 3x + 0, och förenkla tilly = ½x + 0. Är båda ekvationerna identiska, då blir hela linjen en "korsning". Skriva: oändliga lösningar. 
Om du inte har millimeterpapper, använd en linjal för att se till att siffrorna är jämnt fördelade. Om du använder stora siffror eller decimaler kan du behöva skala diagrammet. (Till exempel 10, 20, 30 eller 0.1, 0.2.0.3 istället för 1, 2, 3). 
I de tidigare nämnda exemplen, en rad (y = -2x + 5) i y-axeln 5. Den andra raden (y = ½x + 0) går genom nollpunkten 0. (Detta är punkterna (0,5) och (0,0) i grafen). Markera var och en av linjerna med en annan färg, om möjligt. 
I vårt exempel, regeln y = -2x + 5 en lutning av -2. Vid x = 1 sjunker linjen 2 nerfrån punkten x = 0. Rita linjesegmentet mellan (0,5) och (1,3). Regeln y = ½x + 0har en lutning på ½. Vid x = 1 går linjen ½ upp från punkten x = 0. Rita linjesegmentet mellan (0,0) och (1,½). Om linjerna har samma lutning linjerna kommer aldrig att skära varandra, så det finns ingen lösning för ekvationssystemet. Skriva: ingen lösning. 
Om linjerna rör sig mot varandra kommer du att fortsätta att rita punkter i den riktningen. Om linjerna rör sig bort från varandra, gå tillbaka och rita punkter åt andra hållet, med början på x = -1. Om linjerna inte är i närheten av varandra, hoppa framåt och rita punkter som ligger längre bort, till exempel x = 10. 
Lösa ekvationssystem med två variabler
I ett "ekvationssystem" uppmanas du att lösa två eller flera ekvationer samtidigt. När dessa två innehåller olika variabler, som x och y, eller a och b, kan det vid första anblicken vara svårt att se hur man löser dem. Lyckligtvis, när du väl vet vad du ska göra, behöver du bara några grundläggande matematiska färdigheter (och ibland lite kunskap om bråk) för att lösa problemet. Om det krävs, eller om du är en visuell elev, lär dig också hur man ritar ekvationerna. Att rita (plotta) en graf kan vara användbart för att "se vad som händer", eller för att kontrollera ditt arbete, men det kan också vara långsammare än de andra metoderna och fungerar inte med alla ekvationssystem.
Steg
Metod 1 av 3: Använder substitutionsmetoden

1. Flytta variablerna till olika sidor av ekvationen. Denna `substitution`-metod börjar med att `lösa för x` (eller någon annan variabel) i en av ekvationerna. Till exempel har vi följande ekvationer: 4x + 2y = 8 och 5x + 3x = 9. Låt oss först titta på den första ekvationen. Ordna om genom att subtrahera 2y från varje sida, och du får: 4x = 8 - 2y.
- Denna metod använder ofta fraktioner i ett senare skede. Du kan också använda elimineringsmetoden nedan om du föredrar att inte arbeta med bråk.

2. Dela båda sidor av ekvationen för att `lösa för x`. När du har termen x (eller vilken variabel du använder) på ena sidan av ekvationen, dela båda sidorna av ekvationen för att isolera variabeln. Till exempel:

3. Koppla tillbaka detta till den andra ekvationen. Se till att återvända till Andra jämförelse, inte den du redan har använt. I den ekvationen byter du ut variabeln du löste så att bara en variabel finns kvar. Till exempel:

4. Lös för den återstående variabeln. Du har nu en ekvation med bara en variabel. Använd vanliga algebratekniker för att lösa den variabeln. Om variablerna tar bort varandra, fortsätt till det sista steget. Annars kommer du att få ett svar på en av dina variabler:

5. Använd svaret för att lösa den andra variabeln. Gör inte misstaget att avsluta problemet halvvägs. Du måste ange svaret du fick på nytt i en av de ursprungliga ekvationerna så att du kan lösa den andra variabeln:

6. Vet vad du ska göra när båda variablerna tar bort varandra. När du x = 3y + 2 eller får ett liknande svar i den andra ekvationen, då försöker du få en ekvation med bara en variabel. Ibland får man en ekvation istället utan variabler. Dubbelkolla ditt arbete och se till att ersätta den (omarrangerade) första ekvationen med den andra ekvationen, inte den första ekvationen. När du är säker på att du inte har gjort några misstag får du ett av följande resultat:
Metod 2 av 3: Använder elimineringsmetoden
1. Bestämmer variabeln som ska elimineras. Ibland kommer ekvationerna att "eliminera" varandra i en variabel så snart du adderar dem. Till exempel när du gör ekvationerna 3x + 2y = 11 och 5x - 2y = 13 kombinerar, kommer `+2y` och `-2y` att eliminera varandra, med alla `ys tas bort från ekvationen. Titta på ekvationerna i ditt problem för att ta reda på om någon av variablerna kommer att elimineras på detta sätt. Om ingen av variablerna elimineras, läs vidare till nästa steg för råd.


2. Multiplicera en ekvation för att eliminera en variabel. (Hoppa över detta steg om variablerna redan har eliminerat varandra). Om ingen av variablerna i ekvationerna elimineras av sig själva, måste du modifiera en av ekvationerna så att de gör det. Detta är lättast att förstå med ett exempel:

3. Kombinera de två ekvationerna. För att kombinera två ekvationer, lägg ihop vänster och höger sida. Om du skrev ekvationen rätt, bör en av variablerna ta bort mot den andra. Här är ett exempel som använder samma ekvationer som det sista steget:

4. Lös för den sista variabeln. Förenkla den kombinerade ekvationen och använd sedan grundläggande algebra för att lösa den sista variabeln. Om det inte finns några variabler kvar efter förenklingen, hoppa till det sista steget i detta avsnitt. Annars bör du sluta med ett enkelt svar på en av dina variabler. Till exempel:

5. Lös för de andra variablerna. Du har hittat en variabel, men du är inte riktigt klar än. Ersätt ditt svar med en av de ursprungliga ekvationerna så att du kan lösa den andra variabeln. Till exempel:

6. Vet vad du ska göra om båda variablerna tar bort varandra. Ibland resulterar en kombination av två ekvationer i en ekvation som inte är meningsfull, eller som inte hjälper dig att lösa problemet. Dubbelkolla ditt arbete från början, men om du inte gjorde ett misstag, skriv något av följande svar:
Metod 3 av 3: Rita grafen för ekvationerna

1. Använd endast den här metoden när den är specificerad. Såvida du inte använder en dator eller en grafräknare kan många ekvationssystem endast lösas ungefär med den här metoden. Din lärare eller mattebok kanske ber dig att använda den här metoden, så du är förmodligen bekant med grafiska ekvationer som linjer. Du kan också använda den här metoden för att kontrollera om dina svar från någon av de andra metoderna är korrekta.
- Grundtanken är att man ritar båda ekvationerna och bestämmer punkten där de skär varandra. x- och y-värdena vid denna tidpunkt ger värdet på x och värdet på y i ekvationssystemet.

2. Lös båda ekvationerna för y. Håll de två ekvationerna åtskilda, använd algebra för att omvandla varje ekvation till formen `y = __x + __`. Till exempel:

3. Rita ett koordinatsystem. Rita en vertikal "y-axel" och en horisontell "x-axel" på ett rutpapper. Börja vid den punkt där linjerna skär varandra och märk siffrorna 1, 2, 3, 4 osv. upp längs y-axeln och höger igen längs x-axeln. Märk siffrorna -1, -2 osv. ner längs y-axeln och vänster längs x-axeln.

4. Rita y-skärningen för varje linje. När du har en ekvation i formuläret y = __x + __ du kan börja rita grafen och rita upp en punkt där linjen skär y-axeln. Detta är alltid vid ett y-värde, lika med det sista talet i denna ekvation.

5. Använd lutningen för att fortsätta rita linjerna. I formuläret y = __x + __, är talet för x de backe utanför linjen. Varje gång x ökas med ett, kommer y-värdet att öka med värdet på lutningen. Använd denna information för att hitta punkten på grafen för varje linje, när x = 1. (Alternativt, ersätt x = 1 för valfri ekvation och lös för y).

6. Fortsätt rita linjerna tills de skär varandra. Stanna upp och titta på ditt diagram. Om linjerna redan har korsat varandra, fortsätt till nästa steg. Annars fattar du ett beslut baserat på vad raderna gör:

7. Hitta svaret i skärningspunkten mellan linjerna. När de två linjerna skär varandra är x- och y-värdena vid den punkten lösningen på problemet. Om du har tur blir svaret ett heltal. Till exempel, i våra exempel, skär de två linjerna (2.1) så är ditt svar x = 2 och y = 1. I vissa ekvationssystem kommer linjerna att skära varandra vid ett värde mellan två heltal, och om inte din graf är extremt exakt kommer det att vara svårt att avgöra var detta är. Om så är fallet kan du ge ett svar som: `x är mellan 1 och 2`. Du kan också använda ersättningsmetoden eller elimineringsmetoden för att hitta det exakta svaret.
Tips
- Du kan kontrollera ditt arbete genom att mata tillbaka svaren i de ursprungliga ekvationerna. Om ekvationerna är sanna (till exempel 3 = 3), är ditt svar korrekt.
- I elimineringsmetoden måste man ibland multiplicera en ekvation med ett negativt tal för att eliminera en variabel.
Varningar
- Dessa metoder kan inte användas när det handlar om ett potenstal, såsom x. För mer information om ekvationer av denna typ behöver du en guide till faktorisering av kvadrater med två variabler.
"Lösa ekvationssystem med två variabler"
Оцените, пожалуйста статью