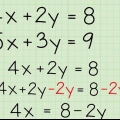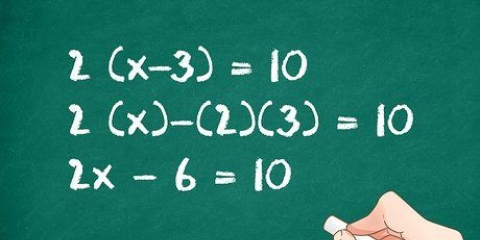3x + 5 + 4x - x + 2x + 9 = 3x - x + 4x + 2x + 5 + 9 = 2x + 6x + 14 
3x + 15 = 9x + 30 Du ser att varje koefficient är delbar med 3. Eliminera talet 3 genom att dividera varje term med 3 för att förenkla ekvationen. 3x/3 + 15/3 = 9x/3 + 30/3 = x + 5 = 3x + 10 
(3 + 5) x 10 + 4 Först operationerna inom parentes: = (8) x 10 + 4 Sedan ska vi höja makten: = 64 x 10 + 4 Sedan multiplikationen: = 640 + 4 Och slutligen lägger vi till: = 644 
5x + 15 = 65 = 5x/5 + 15/5 = 65/5 = x + 3 = 13 = x = 10 

2x + 12 = 44 Subtrahera först 12 från båda sidor. 2x + 12 -12 = 44 -12 = 2x = 32 Dela nu båda sidor med 2. 2x/2 = 32/2 = x = 16 Lös genom att ta kvadratroten från båda sidorna, eftersom det gör x lika med x. √x = √16 = Ge båda svaren: x = 4, -4 
(x + 3)/6 = 2/3 Först ska du multiplicera korsvis för att bli av med bråket. Multiplicera täljaren för ett bråk med nämnaren för det andra bråket. (x + 3) x 3 = 2 x 6 = 3x + 9 = 12 Sedan kombinerar man lika termer. Kombinera de konstanta termerna 9 och 12 genom att subtrahera 9 från båda sidor. 3x + 9 - 9 = 12 - 9 = 3x = 3 Isolera variabeln, x, genom att dividera båda sidor med 3 och du har svaret. 3x/3 = 3/3 = x = 1 
√(2x+9) - 5 = 0 Flytta först allt som inte ligger under radikalen till andra sidan av ekvationen: √(2x+9) = 5 Kvadra sedan båda sidorna för att ta bort radikalen: (√(2x+9)) = 5 = 2x + 9 = 25 Nu kan du lösa ekvationen som vanligt, genom att kombinera konstanterna och isolera variabeln: 2x = 25 - 9 = 2x = 16 x = 8 
Så här räknar du ut detta för det absoluta värdet genom att isolera det absoluta värdet och sedan ta bort det: |4x +2| - 6 = 8 = |4x +2| = 8 + 6 = |4x +2| = 14 = 4x + 2 = 14 = 4x = 12 x = 3 Lös detta igen genom att invertera termens tecken på andra sidan av ekvationen, efter att du har isolerat det absoluta värdet: |4x +2| = 14 = 4x + 2 = -14 4x = -14 -2 4x = -16 4x/4 = -16/4 = x = -4 Ge nu båda svaren: x = -4, 3
Lösa ett algebraiskt uttryck
Ett algebraiskt uttryck är ett matematiskt uttryck som innehåller tal och/eller variabler. Även om det inte går att lösa eftersom det inte innehåller ett likhetstecken (=), kan det förenklas. Däremot kan du lösa matematiska ekvationer, som innehåller algebraiska uttryck åtskilda av ett likhetstecken. Om du vill bemästra detta matematiska koncept, läs vidare till steg 1 för att komma igång.
Steg
Del 1 av 2: Förstå grunderna

1. Förstå skillnaden mellan ett algebraiskt uttryck och en algebraisk ekvation. Ett algebraiskt uttryck är ett matematiskt uttryck som innehåller tal och/eller variabler. Det innehåller inget likhetstecken och kan inte lösas. Men en algebraisk ekvation kan lösas och involverar en serie algebraiska uttryck åtskilda av ett likhetstecken. Här är några exempel:
- Algebraiska uttryck: 4x + 2
- Algebraisk ekvation: 4x + 2 = 100

2. Lär dig hur du kombinerar liknande termer. Att kombinera liknande termer betyder helt enkelt att man adderar (eller subtraherar) termerna av samma grad. Detta innebär att alla x-termer kan kombineras med andra x-termer, alla x-termer kan kombineras med x-termer och alla konstanter (tal som inte är kopplade till variabler, som 8 eller 5) kan också läggas ihop, eller kombineras med varandra. Här är ett exempel:

3. Lär dig hur du faktorisera ett tal. Om du har att göra med en algebraisk ekvation, vilket betyder att det finns ett uttryck på vardera sidan av ett likhetstecken, kan du förenkla detta genom att eliminera den vanliga termen. Titta på koefficienterna för alla villkor (talen före variablerna eller konstanterna) och se om det finns ett tal du kan "arbeta bort" genom att dividera varje term med det talet. Om du kan göra detta, då har du förenklat ekvationen och du är på väg att lösa den. Så här fungerar det här:

4. Känn till ordningen på operationerna. Operationsordningen, även känd som mnemoniken "How To Get Rid Of Die Insufficients", anger i vilken ordning du ska utföra de olika matematiska operationerna. Ordningen är: parentes, exponentiering, rotning, multiplikation, division, addition och subtraktion. Här är ett exempel på hur operationsordningen fungerar:

5. Lär dig att isolera en variabel. Om du vill lösa en algebraisk ekvation är ditt mål att få variabeln, ofta känd som x, på ena sidan av ekvationen och de konstanta termerna på den andra sidan av ekvationen. Du kan isolera x genom att dividera, multiplicera, addera, subtrahera, bestämma kvadratroten eller andra operationer. När du har isolerat x kan du börja lösa det. Så här gör du:
Del 2 av 2: Lösa en algebraisk ekvation

1. Lös en enkel linjär algebraisk ekvation. En linjär algebraisk ekvation är trevlig och enkel, med endast första gradens konstanter och variabler (inga potenser eller annan komplexitet). För att lösa detta behöver du bara multiplicera, dividera, addera eller subtrahera vid behov, isolera variabeln och lösa för `x`. Så här gör du:
- 4x + 16 = 25 -3x =
- 4x = 25 -16 - 3x
- 4x + 3x = 25 -16 =
- 7x = 9
- 7x/7 = 9/7 =
- x = 9/7

2. Lös en algebraisk ekvation med potenser (exponenter). Om ekvationen har potenser är allt du behöver göra att hitta ett sätt att isolera potensen på ena sidan av ekvationen och sedan lösa det genom att "ta bort" potensen genom att hitta kvadratroten av både potensen och konstant på andra sidan av ekvationen. Så här gör du:

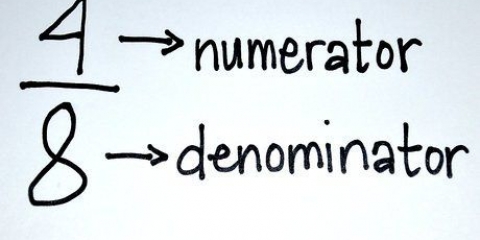
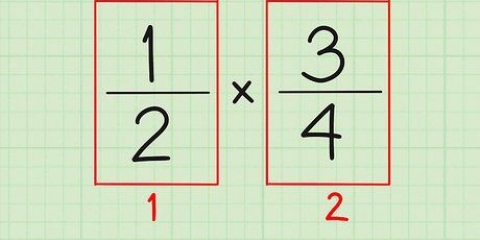
3. Lös ett algebraiskt uttryck med bråk. För att lösa ett algebraiskt uttryck som innehåller bråk, måste du korsmultiplicera bråken, kombinera liknande termer och sedan isolera variabeln. Så här gör du:

4. Lös ett algebraiskt uttryck. Om du har att göra med ett algebraiskt uttryck med radikaler, är allt du behöver göra att hitta ett sätt att kvadrera båda sidorna så att du kan eliminera radikalen för att lösa variabeln. Så här gör du:

5. Lös ett algebraiskt uttryck som innehåller ett absolut värde. Ett tals absoluta värde representerar dess värde oavsett om det är positivt eller negativt; det absoluta värdet är alltid positivt. Så till exempel är absolutvärdet av -3 (även känd som |3|) bara 3. För att hitta det absoluta värdet, isolera det absoluta värdet och lös sedan x två gånger (både för x där absolutvärdet helt enkelt tas bort, och för x där termerna på andra sidan likhetstecknet har ändrat tecken, från positivt till negativt och vice versa). Det här går så här:
Tips
- För att dubbelkolla ditt svar kan du gå till wolfram-alpha.com gå. Där kan du få svaret, ofta visas i de två stegen.
- När du är klar byter du ut variabeln med svaret och löser sedan summan för att se om den är korrekt. Om så är fallet, grattis, du är klar! Du har precis löst en algebraisk ekvation!
- Graden av ett polynom är den högsta potensen inom termerna.
"Lösa ett algebraiskt uttryck"
Оцените, пожалуйста статью