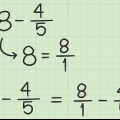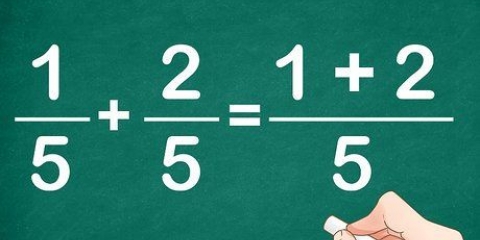18 ÷ 3 = 6, alltså 2/3 = (2x6)/(3x6)=12/18 18 ÷ 6 = 3, alltså 5/6 = (5x3)/(6x3)=15/18 18 ÷ 3 = 6, så 1/3 = (1x6)/(3x6)=6/18 

6/18 = (6 6)/(18 ÷ 6) = 1/3 12/18 = (12 6)/(18 ÷ 6) = 2/3 15/18 = (15 3)/(18 ÷ 3) = 5/6 Svaret är "1/3, 2/3, 5/6" 

Detta kallas korsmultiplikation, eftersom du multiplicerar siffror diagonalt. 



Kom ihåg att alltid placera produkten av multiplikationen bredvid bråket vars täljare du använde. 
3/5=(3x3)/(5x3)=9/15 2/3=(2x5)/(3x5)=10/15 9/15 är mindre än 10/15 Så 3/5 är mindre än 2/3 

8/3 = 2 + 2/3 9/9 = 1 19/4 = 4 + 3/4 13/6 = 2 + 1/6 
1 är den minsta 2 + 2/3 och 2 + 1/6 (vi vet inte vilken som är större än den andra ännu) 4 + 3/4 är störst 
2/3 = (2x2)/(3x2) = 4/6 1/6 = 1/6 4/6 är större än 1/6 2 + 4/6 är större än 2 + 1/6 2 + 2/3 är större än 2 + 1/6 

Sortera fraktioner efter storlek
Även om det är lätt att ordna heltal som 1, 3 och 8 efter storlek, är det inte alltid självklart med bråk. Om varje nämnare är lika kan du beställa dem precis som heltal, t.ex. 1/5, 3/5 och 8/5. I andra fall kan du konvertera bråken så att de får samma nämnare, utan att ändra värdet på bråket. Detta blir lättare med övning och du kan använda några praktiska knep, både när du jämför två bråk eller när du beställer bråk där täljaren är större än nämnaren, de oegentliga bråken som 7/3.
Steg
Metod 1 av 3: Ordna valfritt antal bråk

1. Hitta en lika stor nämnare för alla bråk. Använd en av följande metoder för att hitta en nämnare, eller minska antalet av ett bråk, som du kan använda för att skriva om varje bråk i listan för enkel jämförelse. Detta är vad du kallar a gemensam nämnare, eller den minsta gemensamma nämnare om detta är minsta möjliga:
- Multiplicera varje nämnare tillsammans. Om du till exempel jämför 2/3, 5/6 och 1/3, multiplicera dessa nämnare: 3 x 6 = 18. Detta är en enkel metod men en som ofta resulterar i ett mycket större antal än de andra metoderna, som är lite knepigare.
- Eller lista multiplar av varje nämnare i en separat kolumn, tills ett tal som förekommer oftare sticker ut. Till exempel, vid 2/3, 5/6 och 1/3 har du listmultiplar av 3:3, 6, 9, 12, 15, 18. Sedan en lista med multiplar av 6: 6, 12, 18. Eftersom 18 förekommer i båda listorna, använd det numret (Du kan också använda 12, men exemplen nedan förutsätter att du använder 18).

2. Konvertera varje bråk så att de får en lika stor nämnare. Kom ihåg att om du multiplicerar täljaren och nämnaren för ett bråk med samma tal, förblir värdet på bråket detsamma. Använd denna teknik med varje bråk, en i taget, så att varje bråk har samma nämnare. Prova detta för 2/3, 5/6 och 1/3, med nämnaren 18:

3. Ordna bråken efter täljare. Nu när alla bråk har samma nämnare är de lätta att jämföra. Beställ dem från minsta till största enligt disken. Detta ger oss följande lista: 18/6, 18/12, 15/18.

4. Återställ varje bråk till sin ursprungliga form. Lämna bråken i denna ordning, men konvertera dem tillbaka till den ursprungliga bråkdelen. Du gör detta genom att helt enkelt komma ihåg vilket bråk som hör till vilket eller genom att dela bråkets översta och nedersta nummer igen:
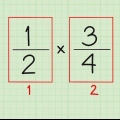
Metod 2 av 3: Ordna två bråk med korsmultiplikation

1. Skriv de två bråken sida vid sida. Jämför till exempel bråket 3/5 och bråket 2/3. Skriv dessa sida vid sida: 3/5 till vänster och 2/3 till höger.

2. Multiplicera täljaren för det första bråket med nämnaren för det andra. Alltså: 3 x 3 = 9.

3. Skriv ditt svar bredvid den första bråkdelen. Skriv produkten av 3 x 3 = 9, bredvid det första bråket.

4. Multiplicera täljaren för andra bråkdel med nämnaren av först. För att se vilken som är störst jämför vi svaret med en annan multiplikation. Multiplicera dessa två tal tillsammans. I det här exemplet (vi jämför 3/5 och 2/3) multiplicerar vi 2 x 5.

5. Skriv svaret bredvid den andra bråkdelen. Skriv resultatet av 2 x 5 =10 bredvid den andra bråkdelen.

6. Jämför värdena på resultaten. Om det ena värdet är större än det andra är andelen bredvid resultatet också störst. Så eftersom 9 är mindre än 10, är 3/5 mindre än 2/3.

7. Hur exakt fungerar detta? Det du gör är att konvertera bråken så att de båda har samma nämnare. Så detta är vad korsmultiplikation faktiskt gör! Det hoppar faktiskt över att skriva ner nämnare eftersom du bara behöver jämföra täljarna vid liknande nämnare. Så som följer, utan den korta vägen för korsmultiplikation:
Metod 3 av 3: Ordna bråk större än en

1. Använd den här metoden för bråk där täljaren är större än nämnaren. Om täljaren är större än nämnaren är denna bråkdel större än 1. 8/3 är ett exempel på detta. Du kan också använda detta för bråk med samma täljare och nämnare, till exempel 9/9. Dessa är båda exempel på "felaktig" fraktioner.
- Du kan fortfarande använda de andra metoderna för dessa fraktioner. Denna metod hjälper dig att förstå dessa bråk bättre och kan vara lite snabbare.

2. Konvertera en oegentlig fraktion till en blandad fraktion. Gör det till en kombination av ett heltal och ett bråk. Ibland kan du enkelt göra detta utantill. Till exempel, 9/9 = 1. I de svårare fallen, använd lång division för att ta reda på hur många gånger nämnaren är delbar med täljaren. Den möjliga återstoden av den långa divisionen finns kvar som en bråkdel. Till exempel:

3. Sortera de blandade talen efter hela talet. Nu när det inte finns fler felaktiga bråk, har du en bättre uppfattning om storleken på varje nummer. Ignorera bråken först och sortera varje blandat tal efter heltal:

4. Jämför bråken i varje grupp om det behövs. Om du har flera blandade tal med samma heltal, till exempel 2 + 2/3 och 2 + 1/6, jämför bråkdelen av båda talen för att ta reda på vilket som är störst. I exemplet jämför vi 2 + 2/3 och 2 + 1/6 och omvandlar bråken till samma nämnare:

5. Använd resultatet för att ytterligare sortera listan med blandade nummer. Ordningen på hela listan blir nu: 1, 2 + 1/6, 2 + 2/3, 4 + 3/4.

6. Konvertera de blandade talen tillbaka till de ursprungliga bråken. Behåll ordningen densamma, men ångra alla ändringar och skriv om bråken som de ursprungliga oegentliga bråken: 9/9, 8/3, 13/6, 19/4.
Tips
- Vid sekvensering av ett stort antal fraktioner kan det vara användbart att jämföra små grupper om 2, 3 eller 4 fraktioner.
- Även om det kan vara till hjälp att hitta den minsta gemensamma nämnaren, fungerar vilken gemensam nämnare som helst. Försök att ranka 2/3, 5/6 och 1/3 med en gemensam nämnare på 36 och se om du får samma resultat.
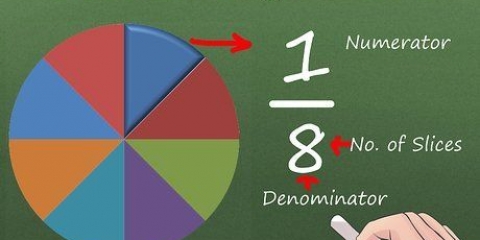
- Om täljarna är lika kan du också snabbt beställa bråken. Till exempel 1/8 < 1/7 < 1/6 < 1/5. Tänk på det här som om det vore en pizza: om du går från 1/2 till 1/8 skär du pizzan i 8 bitar istället för 2 och bitarna blir mindre.
"Sortera fraktioner efter storlek"
Оцените, пожалуйста статью