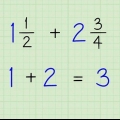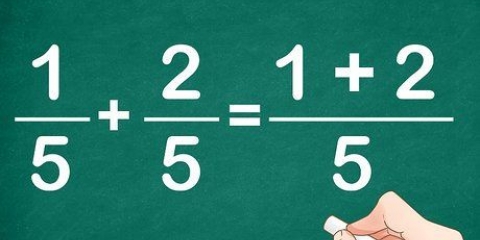Ex. 1: 1/4 + 2/4
Ex. 2: 3/8 + 2/8 + 4/8
Ex. 1: 1/4 + 2/4 är vår ekvation. "1" och"2" är räknarna. Det betyder 1 + 2 = 3.
Ex. 2: 3/8 + 2/8 + 4/8 är vår ekvation. "3" och"2" och"4" är räknarna. Det betyder 3 + 2 + 4 = 9.
Ex. 1: 3 är vår nya täljare och 4 är den "nya" nämnaren. Detta ger svaret: 3/4. 1/4 + 2/4 = 3/4.
Ex. 2: 9 är vår nya täljare och 8 är den "nya" nämnaren. Detta ger svaret: 9/8. 3/8 + 2/8 + 4/8 = 9/8.
Om täljaren är större än nämnaren, som i t.ex. 2, då kan åtminstone ett heltal tas bort från bråket. Dividera täljaren med nämnaren. Om vi dividerar 9 med 8 får vi 1 heltal och resten av 1. Sätt hela talet före bråket och resten som täljare för det nya bråket, håll nämnaren oförändrad.9/8 = 1 1/8.

Ex. 3: 1/3 + 3/5
Ex. 4: 2/7 + 2/14
Ex. 3: 3 x 5 = 15. Båda bråken har 8 som nämnare.
Ex. 4: 14 är en multipel av 7. Så vi behöver bara multiplicera 7 med 2 för att få 14. Båda bråken har då nämnaren 14.
Ex. 3: 1/3 x 5/5 = 5/15.
Ex. 4: För det här bråket behöver vi bara multiplicera det första bråket med 2, för på så sätt kan vi få den gemensamma nämnaren.
2/7 x 2/2 = 4/14. Ex. 3: 3/5 x 3/3 = 9/15.
Ex. 4: Det andra bråket behöver inte multipliceras eftersom båda bråken redan har samma nämnare. Ex. 3: istället för 1/3 + 3/5 har vi 5/15 + 9/15
Ex. 4: istället för 2/7 + 2/14 har vi 4/14 + 2/14
Ex. 3: 5 + 9 = 14. 14 blir den nya räknaren.
Ex. 4: 4 + 2 = 6. 6 blir den nya räknaren.
Ex. 3: 15 blir vår nya nämnare.
Ex. 4: 14 blir vår nya nämnare.
Ex. 3: 14/15 är vårt nya svar på 1/3 + 3/5 = ?
Ex. 4: 6/14 är vårt svar på 2/7 + 2/14 = ?
Ex. 3: 14/15 kan inte förenklas.
Ex. 4: 6/14 kan reduceras till 3/7 genom att dividera både täljaren och nämnaren med 2, den största gemensamma divisorn.
Lägg ihop fraktioner
Att kunna lägga till bråk är en mycket användbar färdighet. Inte bara för grundskolan och gymnasiet, det är bara en mycket praktisk färdighet. Läs mer om att lägga till bråk här. Du kommer att bli förvånad över vad du kan lära dig på några minuter.
Steg
Metod 1 av 2: Del ett: Lägga till bråk med samma nämnare

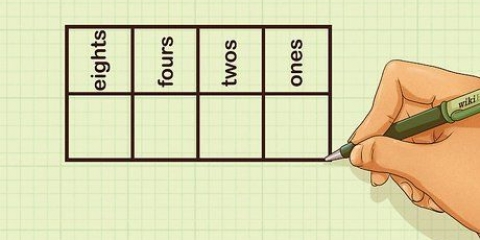
1. Kontrollera nämnarna (talen under linjen) för varje bråkdel. Om de har samma nummer, så har du att göra med bråk med lika nämnare. Om inte, hoppa över nästa avsnitt.
2. Här är två exempel på frågor som vi kommer att arbeta med i det här avsnittet. När du kommer till det sista steget bör du förstå hur addition fungerar.


3. Ta de två täljarna (siffrorna ovanför linjen) och lägg ihop dem. Det spelar ingen roll hur många bråk du har, om de har samma nämnare kan du bara lägga ihop alla täljare.


4. Konstruera den nya fraktionen. Ta summan av täljarna du fick i steg 2; denna summa blir den nya disken. Använd nämnaren för bråken från föregående steg. Detta kommer att vara den nya nämnaren; denna nämnare förblir alltid densamma när du lägger till bråk med samma nämnare


5. Förenkla om du kan. Förenkla den nya bråkdelen för att se till att siffrorna är så små som möjligt.

Metod 2 av 2: Del två: Lägga till bråk med ojämna nämnare

1. Kontrollera nämnare (tal under bråklinjen) för varje bråk. Om nämnarna är ojämlika måste du hitta ett sätt att göra dem lika. Läs vidare för att lära dig hur.
2. Här är två exempel på problem som vi kommer att arbeta med i det här avsnittet. När vi kommer till det sista steget vet du hur man lägger ihop bråk med olika nämnare.


3. Hitta en lämplig nämnare. Du kan göra detta genom att leta efter den gemensamma multipeln av nämnarna. Ett enkelt sätt att hitta det är att helt enkelt multiplicera båda nämnarna. Om en av nämnarna är en multipel av den andra, behöver du bara multiplicera den andra bråkdelen.


4. Multiplicera båda talen i det första bråket med nämnaren i det andra bråket. Det finns ingen förändring i bråkets värde; vi ändrar bara hur bråket ser ut. Det är fortfarande samma bråkdel.


5. Multiplicera båda talen i det andra bråket med nämnaren i det första bråket. Återigen, vi ändrar inte värdet på bråket, bara hur det ser ut. Det är fortfarande samma bråkdel.

6. Placera båda bråken bredvid varandra med sina nya tal. De har inte lagts ihop än, bara lite tålamod! Det vi har gjort är att multiplicera varje bråkdel med ett lämpligt tal, med målet att göra båda nämnarna lika.


7. Lägg ihop täljarna för båda bråken.


8. Ta den lika nämnaren du beräknade i steg 2 och använd den som nämnaren för det nya bråket. Detta är förresten givetvis samma nämnare som du redan ser i det ändrade bråket.




9. Förenkla bråket. Förenkla bråket genom att dividera både täljaren och nämnaren med den största gemensamma divisorn.


Tips
Оцените, пожалуйста статью