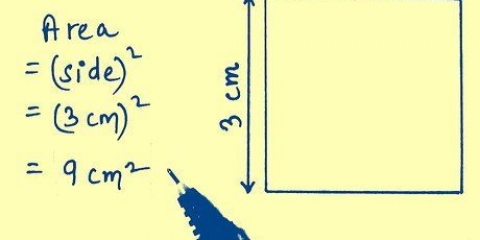
(Z = √(60² + 60²)). Så om du anger det i din vetenskapliga kalkylator blir svaret 84,85Ω. (Z = 84,85Ω). 
Du har då en ekvation som: (60/60 = 1) 




Detta kan också uttryckas i procent, så du multiplicerar 0,460 med 100, vilket ger en effektfaktor på 46 %.
Beräkna effektfaktorkorrigeringen
Genom effektfaktorkorrigeringen kan du beräkna skenbar effekt, effekt, reaktiv effekt och fasvinkel. Betrakta ekvationen för en rätvinklig triangel. För att beräkna en vinkel måste du veta vad cosinus, sinus och tangent är. Du måste också använda Pythagoras sats (c² = a² + b² ) för att beräkna dimensionerna på triangelns sidor. Du måste också veta vilka enheter varje typ av förmåga har. Skenbar effekt mäts i Volt-Ampère. Effekt mäts i Watt och reaktiv effekt uttrycks i Volt-Amp Reactive (VAR) enheter. Det finns flera ekvationer för att beräkna dessa och alla kommer att behandlas i den här artikeln. Du har nu grunden för vad du försöker beräkna.
Steg

1. Beräkna impedansen. (Låtsasimpedansen är på samma plats som den skenbara kraften i bilden ovan). För att bestämma impedansen använder du Pythagoras sats, c² = √ (a² + b²).

2. Den totala impedansen (representerad som `Z`) är alltså lika med effekten i kvadrat plus den reaktiva effekten i kvadrat, då tar du kvadratroten av svaret.

3. Bestäm fasvinkeln. Så nu har du hypotenusan, som är impedansen. Du har också en intilliggande sida, kraften, och du har den motsatta sidan, den reaktiva effekten. Så för att hitta vinkeln kan du använda en av formlerna som nämnts tidigare. Till exempel använder vi tangentformeln, d.v.s. motsatt sida dividerad med intilliggande (reaktiv/effekt).

4. Ta det reciproka av tangenten för fasvinkeln. Den omvända tangenten är en knapp på din miniräknare. Så ta nu den inversa tangenten av ekvationen i föregående steg och du får fasvinkeln. Din ekvation bör se ut ungefär så här: tan ‾ ¹ (1) = fasvinkel. ditt svar blir då 45°.

5. Beräkna den totala strömmen (Ampere). Strömmen visas också som ett `A` i enheten Ampere. Formeln som används för att beräkna strömmen är spänningen dividerad med impedansen, så detta är: 120V/84,85Ω. Du har nu ett svar på cirka 1,141A. (120V/84,84Ω = 1,141A).

6. Du måste nu beräkna den skenbara effekten som visas som `S`. Du behöver inte använda Pythagoras sats för att beräkna skenbar kraft eftersom din hypotenusa anses vara din impedans. Kom ihåg att skenbar effekt använder enheten Volt-Ampere: vi kan beräkna den skenbara effekten med formeln: Spänning i kvadrat dividerat med den totala impedansen. Din ekvation bör se ut så här: 120V²/84,85Ω. Nu bör du få ett svar som: 169.71VA. (120²/84,85 = 169,71).

7. Du måste nu beräkna effekten som visas som `P`. För att beräkna effekten behöver du strömmen som du gjorde i steg fyra. Effekten är i watt och beräknas genom att multiplicera strömmen i kvadrat (1,141²) med motståndet (60Ω) i din krets. Du bör få ett svar på 78,11 watt. Ekvationen ska se ut så här: 1,141² x 60 = 78,11.

8. Beräkna effekt eller effektfaktor! För att beräkna effektfaktorn behöver du följande information: Watt och Volt-Amp. Du beräknade denna information i de föregående stegen. Effekten är lika med 78,11W och Volt-Ampère är 169,71VA. Formeln för effektfaktorn, även representerad som Pf, är watt dividerat med Volt-Amp. Din ekvation ser nu ut så här: 78.11/169.71 = 0.460.
Varningar
- När du beräknar impedans använder du den inversa tangentfunktionen och inte bara den vanliga tangentfunktionen på din miniräknare. Annars får du en felaktig fasvinkel.
- Detta var bara ett mycket enkelt exempel på att beräkna en fasvinkel och effektfaktor. Det finns mycket mer komplicerade kretsar, inklusive kapacitanseffekt och högre resistanser och impedans.
Förnödenheter
- Vetenskaplig kalkylator
- Penna
- Suddgummi
- Papper
"Beräkna effektfaktorkorrigeringen"
Оцените, пожалуйста статью