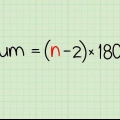Om du till exempel vill beräkna summan av serierna 10, 15, 20, 25, 30,  , eftersom det finns fem nummer i sekvensen.
, eftersom det finns fem nummer i sekvensen. 
Till exempel i sekvensen 10, 15, 20, 25, 30  , och
, och  .
. 

Till exempel, om det finns fem siffror i din sekvens, där 10 är den första siffran och 30 är den sista siffran, kommer din formel att se ut så här:  .
. 
Till exempel:



Till exempel:


Så summan av serien (10, 15, 20, 25, 30) är lika med 100. 

Bestäm antalet siffror ( ) i serien. Eftersom du börjar med tre, slutar med 24 och lägger till sju varje gång, är talföljden 3, 10, 17, 24. (Skillnadsfaktorn är skillnaden mellan varje nummer i serien.) Detta innebär att
) i serien. Eftersom du börjar med tre, slutar med 24 och lägger till sju varje gång, är talföljden 3, 10, 17, 24. (Skillnadsfaktorn är skillnaden mellan varje nummer i serien.) Detta innebär att 
Bestäm den första ( ) och sist (
) och sist ( ) nummer i sekvensen. Eftersom sekvensen är 3 till 24,
) nummer i sekvensen. Eftersom sekvensen är 3 till 24,  och
och  .
. Hitta medelvärdet av  och
och  :
:  .
. Multiplicera medelvärdet med  :
:  .
. 
Bestäm antalet termer ( ) i serien. Eftersom Mara sparar i 52 veckor, (1 år),
) i serien. Eftersom Mara sparar i 52 veckor, (1 år),  .
. Bestäm den första ( ) och sist (
) och sist ( ) nummer i sekvensen. Det första beloppet hon sparar är fem euro, alltså
) nummer i sekvensen. Det första beloppet hon sparar är fem euro, alltså  . För att beräkna det totala beloppet som sparats under årets sista vecka, räknar vi
. För att beräkna det totala beloppet som sparats under årets sista vecka, räknar vi  . så
. så  .
. Bestämmer medelvärdet av  och
och  :
:  .
. Multiplicera medelvärdet med  :
:  . Så hon sparade €6890 i slutet av året.
. Så hon sparade €6890 i slutet av året.
Hitta summan av en aritmetisk sekvens
En aritmetisk sekvens är en talföljd där varje tal ökar med ett konstant värde. För summan av en aritmetisk sekvens kan du lägga till alla siffror tillsammans. Detta är dock inte riktigt praktiskt när sekvensen innehåller ett stort antal termer. Istället kan du snabbt hitta summan av varje aritmetisk sekvens genom att multiplicera medelvärdet av det första och sista talet med antalet termer i sekvensen.
Steg
Del 1 av 3: Analysera din sekvens

1. Se till att du har en aritmetisk sekvens. En aritmetisk sekvens är en ordnad lista med tal, där förändringen av talen är konstant. Den här metoden fungerar bara om din uppsättning siffror är en aritmetisk sekvens.
- För att avgöra om du har att göra med en aritmetisk sekvens, hitta skillnaden mellan det första eller sista paret av tal. Se till att skillnaden alltid är densamma.
- Till exempel är talföljden 10, 15, 20, 25, 30 en aritmetisk följd, eftersom skillnaden mellan varje nummer konstant är fem.

2. Bestäm antalet termer i din sekvens. Varje tal är en term. Om bara ett nummer nämns kan du räkna dem. Om du känner till den första siffran, den sista siffran och skillnadsfaktorn (skillnaden mellan varje nummer), kan du använda en formel för att bestämma antalet siffror. Detta nummer presenteras av variabeln  .
.
 .
. , eftersom det finns fem nummer i sekvensen.
, eftersom det finns fem nummer i sekvensen.
3. Hitta den första och sista siffran i sekvensen. Du måste känna till båda siffrorna för att beräkna summan av den aritmetiska sekvensen. Ofta är den första siffran ett, men inte alltid. Ställ in variabeln  lika med det första talet i sekvensen, och
lika med det första talet i sekvensen, och  lika med den sista siffran i sekvensen.
lika med den sista siffran i sekvensen.
 lika med det första talet i sekvensen, och
lika med det första talet i sekvensen, och  lika med den sista siffran i sekvensen.
lika med den sista siffran i sekvensen. , och
, och  .
.Del 2 av 3: Beräkna summan

1. Skriv formeln för att hitta summan av en aritmetisk följd. Formeln är  , varigenom
, varigenom  är lika med summan av serien.
är lika med summan av serien.
 , varigenom
, varigenom  är lika med summan av serien.
är lika med summan av serien. - Observera att denna formel indikerar att summan av den aritmetiska sekvensen är lika med medelvärdet av det första och sista talet multiplicerat med antalet siffror.

2. Ange värdena n  ,
, a 1  och
och a n  i formeln i. Se till att du byter ut rätt.
i formeln i. Se till att du byter ut rätt.
 ,
,  och
och  i formeln i. Se till att du byter ut rätt.
i formeln i. Se till att du byter ut rätt. .
.
3. Beräkna medelvärdet av det första och andra talet. Det gör du genom att lägga ihop de två talen och dividera med två.



4. Multiplicera medelvärdet med antalet tal i serien. Detta ger dig summan av den aritmetiska sekvensen.


Så summan av serien (10, 15, 20, 25, 30) är lika med 100.
Del 3 av 3: Slutföra provproblemen

1. Hitta summan av talen från 1 till 500. Inkludera alla på varandra följande heltal i beräkningen.
- Bestäm antalet termer (
) i serien. Eftersom du räknar alla på varandra följande heltal upp till och med 500,
.
- Bestäm den första (
) och sist (
) nummer i sekvensen. Eftersom vi antar serien 1 till 500, så gäller det
och
.
- Hitta medelvärdet av
och
:
.
- Multiplicera medelvärdet med
:
.

2. Hitta summan av den angivna aritmetiska sekvensen. Den första siffran i sekvensen är tre. Den sista siffran i sekvensen är 24. Skillnadsfaktorn är sju.
 ) i serien. Eftersom du börjar med tre, slutar med 24 och lägger till sju varje gång, är talföljden 3, 10, 17, 24. (Skillnadsfaktorn är skillnaden mellan varje nummer i serien.) Detta innebär att
) i serien. Eftersom du börjar med tre, slutar med 24 och lägger till sju varje gång, är talföljden 3, 10, 17, 24. (Skillnadsfaktorn är skillnaden mellan varje nummer i serien.) Detta innebär att 
 ) och sist (
) och sist ( ) nummer i sekvensen. Eftersom sekvensen är 3 till 24,
) nummer i sekvensen. Eftersom sekvensen är 3 till 24,  och
och  .
. och
och  :
:  .
. :
:  .
.
3. Lös följande problem. Mara sparar 5 euro första veckan på året. Resten av året ökar hon sitt sparande med 5 euro varje vecka. Hur mycket pengar sparade Mara i slutet av året?
 ) i serien. Eftersom Mara sparar i 52 veckor, (1 år),
) i serien. Eftersom Mara sparar i 52 veckor, (1 år),  .
. ) och sist (
) och sist ( ) nummer i sekvensen. Det första beloppet hon sparar är fem euro, alltså
) nummer i sekvensen. Det första beloppet hon sparar är fem euro, alltså  . För att beräkna det totala beloppet som sparats under årets sista vecka, räknar vi
. För att beräkna det totala beloppet som sparats under årets sista vecka, räknar vi  . så
. så  .
. och
och  :
:  .
. :
:  . Så hon sparade €6890 i slutet av året.
. Så hon sparade €6890 i slutet av året. "Hitta summan av en aritmetisk sekvens"
Оцените, пожалуйста статью