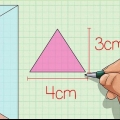
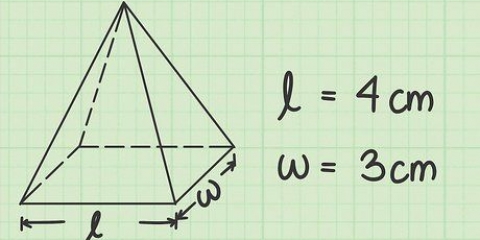Ex: om höjden på den triangulära basen är 5 cm och basen på det triangulära prismat är 4 cm, då är basens yta 1/2 x 5 cm x 4 cm, lika med 10 cm. 

Ex: 10 cm x 7 cm = 70 cm 


Ex: Längd = 3 cm. 
Ex: 3 cm = 3 cm. * 3 cm. * 3 cm. = 27 cm. 


Ex: Längd = 10 cm. 
Ex: Bredd = 8 cm. 
Ex: Höjd = 5 cm. 
Ex: 10 cm. *8 cm. * 5cm = 400cm. 


Anta att bas 1 = 8 cm, bas 2 = 6 cm och höjd = 10 cm. Ex: 1/2 x (6 + 8) x 10 = 1/2 x 14 cm x 10 cm = 80 cm. 

80cm x 12cm = 960cm. 


A = 1/2 x 5 x sida x apotem A = 1/2 x 5 x 6 cm x 7 cm = 105 cm 

105 cm x 10 cm = 1050 cm 
Beräkna volymen av ett prisma
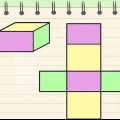
Ett prisma är en geometrisk figur med två identiska ändar och plana sidor. Prismat är uppkallat efter formen på dess bas, så ett prisma med en triangulär bas kallas för a "trekantsprisma." För att beräkna volymen av ett prisma behöver du bara beräkna basens area och multiplicera den med höjden - att beräkna basens area kan vara den svåra delen. Så här beräknar du volymen av olika prismor.
Steg
Metod 1 av 5: Beräkna volymen av ett triangulärt prisma

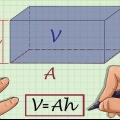
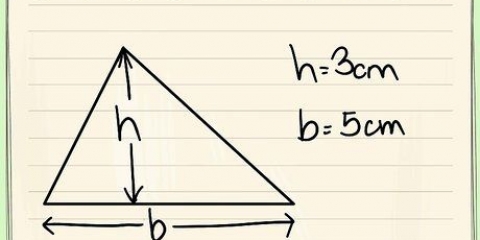
1. Skriv formeln för att hitta volymen av ett triangulärt prisma. Formeln är V = 1/2 x längd x bredd x höjd. Men vi bryter ner den här formeln ytterligare för att få formeln V = area eller bas x höjd att använda. Du kan beräkna arean av basen med hjälp av formeln för att hitta arean av en triangel - multiplicera 1/2 med basens längd och bredd.

2. Bestäm arean av basplanet. För att hitta volymen av ett triangulärt prisma måste du först bestämma arean av den triangulära basen. Hitta arean av prismats bas genom att multiplicera 1/2 gånger triangelns bas gånger höjden.

3. Bestäm höjden. Antag att höjden på detta triangulära prisma är 7 cm.

4. Multiplicera arean av den triangulära basen gånger höjden. Multiplicera arean av basen gånger höjden. Multiplicera basen med höjden och du får volymen av det triangulära prismat.

5. Ge ditt svar i kubikenheter. Du bör alltid använda kubikenheter när du beräknar en volym eftersom du arbetar med tredimensionella objekt. Slutsvaret är 70 cm.
Metod 2 av 5: Beräkna volymen av en kub

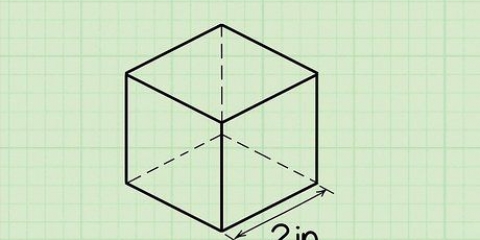
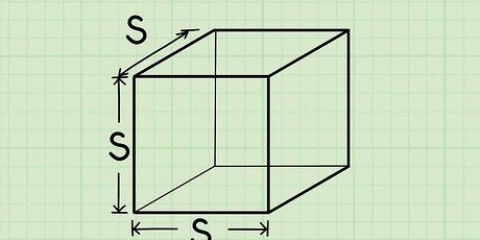
1. Skriv formeln för att hitta volymen av en kub. Formeln är V = sida. En kub är ett prisma med 3 lika sidor.

2. Bestäm längden på 1 sida av kuben. Alla sidor är lika, så det spelar ingen roll vilken du väljer.

3. Kraften i tre. Multiplicera talet med sig själv två gånger för att få kubiktalet. Ett exempel är "a x a x a". Eftersom alla längder på sidorna är lika, multiplicera två sidor för arean av basen och en tredje sida för höjden. Du kan tänka på detta som en multiplikation av längden, bredden och höjden, som alla är desamma.

4. Ge ditt svar i kubikenheter.. Slutsvaret är 27 cm.
Metod 3 av 5: Beräkna volymen av ett rektangulärt prisma

1. Skriv formeln för att hitta volymen av ett rektangulärt prisma. Formeln är V = längd * bredd * höjd. Ett rektangulärt prisma är ett prisma med en rektangulär bas.

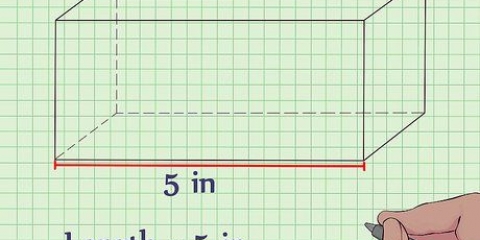
2. Bestäm längden. Längden är den längsta sidan av rektangelns plana yta, ovanför eller under det rektangulära prismat.

3. Bestäm bredden. Bredden på det rektangulära prismat är den kortare sidan av den plana ytan av en rektangel, längst upp eller längst ner på formen.

4. Bestäm höjden. Höjden är den del av det rektangulära prismat som är upprätt. Du kan föreställa dig höjden på det rektangulära prismat som den del som sträcker sig från en rektangel och gör en tredimensionell figur av den.

5. Multiplicera längden, bredden och höjden. Multiplicera dessa i valfri ordning för produkten. Använd den här metoden för att hitta arean av den rektangulära basen (10 x 8) och sedan volymen genom att multiplicera den med höjden, 5. Men för att hitta volymen på detta prisma kan du multiplicera längderna på arena i valfri ordning.

6. Ge ditt svar i kubikenheter. Slutsvaret är 400 cm.
Metod 4 av 5: Beräkna volymen av ett trapetsformat prisma

1. Skriv formeln för att beräkna volymen av en trapets. Formeln är: V = [1/2 x (bas1 + bas2) x höjd] x prismats höjd. Använd den första delen för arean av prismats bas innan du fortsätter.

2. Hitta arean av basen. För att göra detta, skriv in området för toppen och botten i formeln, tillsammans med höjden.

3. Bestäm prismats höjd. Antag att prismats höjd är 12 cm.

4. Multiplicera arean av basen gånger höjden. För att beräkna volymen på trapetsen, multiplicera arean av basen med höjden.

5. Ge ditt svar i kubikenheter. Slutsvaret är 960 cm
Metod 5 av 5: Beräkna volymen av ett vanligt femkantigt prisma

1. Skriv ner formeln för att hitta volymen av ett vanligt femkantigt prisma. Formeln är V = [1/2 x 5 x sida x apotem] x prismats höjd. Du kan använda den första delen av formeln för att hitta arean av den femkantiga basen. Tänk på detta som att bestämma arean av de 5 trianglarna som tillsammans bildar en vanlig polygon. Sidan är bredden på en triangel, och apotem är höjden på en av trianglarna.Du multiplicerar nu med 1/2 eftersom det är en del av att hitta arean av en triangel och sedan multiplicerar du detta med 5 eftersom det finns 5 trianglar i en femhörning.
- För mer information om att bestämma apotem, se här.

2. Hitta arean för den femkantiga basen. Antag att längden på en sida är 6 cm och längden på apotem är 7 cm. Ange siffrorna i formeln:

3. Bestäm höjden. Ställ in höjden på formen är 10 cm.

4. Multiplicera arean av den femkantiga basen gånger höjden. Multiplicera arean av den femkantiga basen, 105 cm, gånger höjden, 10 cm, för att hitta volymen av det vanliga femkantiga prismat.

5. Ge ditt svar i kubikenheter. Slutsvaret är 1050 cm.
Tips
- Prova "bas" inte att förväxla med "basplan".Ett basplan hänvisar till den tvådimensionella form som är basen av prismat (vanligtvis toppen och botten).Men det basplanet kan ha sin egen bas --- en av sidorna av planets form, som används för att hitta arean av den formen.
"Beräkna volymen av ett prisma"
Оцените, пожалуйста статью