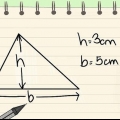
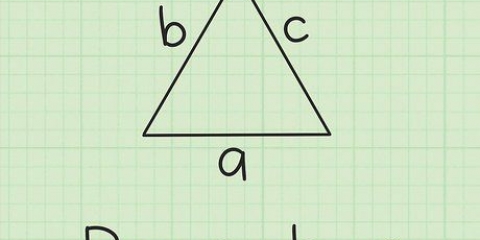
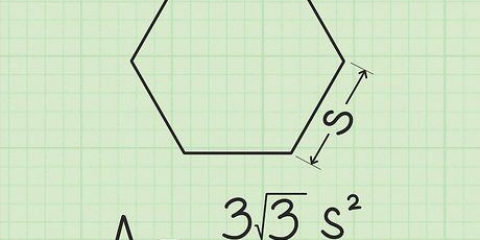
Till exempel, om en likbent triangel har sidor på 5 cm, 5 cm och 6 cm, är sidan på 6 cm basen. Om en triangel har tre lika sidor (och därför är liksidig), kan du välja vilken sida som helst som bas. En liksidig triangel är en speciell sorts likbent triangel, men du kan hitta dess area på samma sätt. 
I en likbent triangel vidrör denna linje alltid basen i dess exakta centrum. 
En av kortsidorna är lika med hälften av basen:  .
. Den andra kortsidan är höjden h. Hypotenusan (hypotenusan) i den räta triangeln är en av de två lika sidorna av den likbenta triangeln. Låt oss ta det här s att nämna. 
Du lärde dig förmodligen Pythagoras sats om  . Genom att skriva detta som "sidor" och "hypotenusa" förhindrar du att du förväxlar dessa med variablerna i triangeln.
. Genom att skriva detta som "sidor" och "hypotenusa" förhindrar du att du förväxlar dessa med variablerna i triangeln. 


 .
.
Till exempel har du en likbent triangel med sidorna 5 cm, 5 cm och 6 cm. b = 6 och s = 5. Använd dessa värden i din formel:





 centimeter.
centimeter. 
För att fortsätta med exemplet: triangeln 5-5-6 har en bas på 6 cm och en höjd på 4 cm. A = bh
A = ½(6cm)(4cm)
A = 12 cm. 
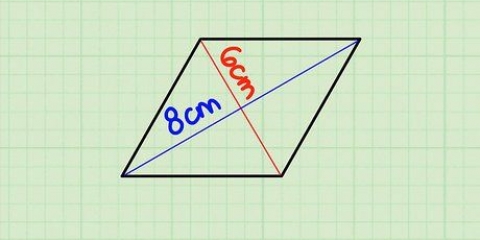
Vad är arean av en triangel med sidorna 8 cm, 8 cm och 4 cm? Den ojämna sidan är 4 cm, och basen b. Höjden 


Förenkla kvadratroten genom att faktorisera: 
Yta 


Lämna svaret som angett, eller använd en miniräknare för en decimaluppskattning (cirka 15,49 cm2). 

Denna linje delar θ perfekt på mitten. Varje rätvinklig triangel har en vinkel på ½θ, eller i detta fall (½)(120) = 60 grader. 
cos(θ/2) = h/s cos(60º) = h / 10 h = 10cos(60º) 
sin(θ/2) = x/s sin(60º) = x / 10 x = 10sin(60º) 





Med hjälp av en miniräknare (inställd på grader) får du cirka 43,3 cm2 som svar. Alternativt kan du använda egenskaperna för trigonometri för att förenkla dem till A = 50sin(1200). 

s är längden på en av de två lika sidorna. Θ är vinkeln mellan de två lika sidorna.
Beräkna arean av en likbent triangel
En likbent triangel är en triangel med två sidor av samma längd. Dessa två lika sidor har alltid samma vinkel mot basen (den tredje sidan), och möts direkt ovanför basens mitt. Du kan testa detta själv med en linjal och två lika långa pennor: om du försöker luta triangeln åt ena hållet kommer ändarna på pennorna inte att mötas. Med dessa speciella egenskaper hos den likbenta triangeln kan arean beräknas med bara några få data.
Steg
Metod 1 av 2: Bestäm arean med hjälp av längderna på varje sida

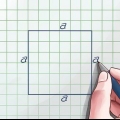
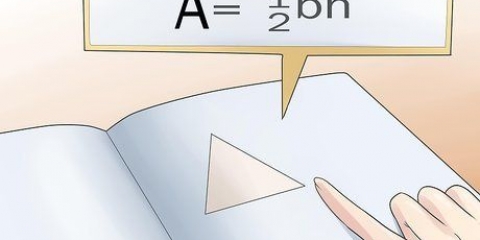
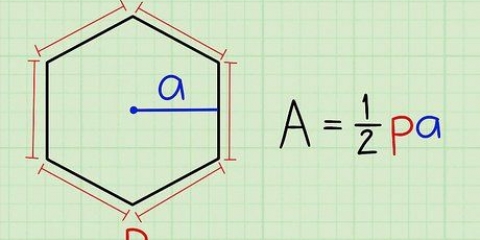
1. Ta arean av ett parallellogram. Kvadrater och rektanglar är parallellogram, som vilken fyrsidig form som helst där två par sidor är parallella med varandra. Alla parallellogram har en enkel areaformel: area är lika med bas multiplicerat med höjd, eller A = bh. Om du placerar ett tänkt parallellogram upprätt på en horisontell yta, är basen längden på sidan figuren är på. Höjden är avståndet från basen till den högsta punkten (som du kan förvänta dig); dvs avståndet från basen till motsatt sida. Mät alltid höjden i rät vinkel (90 grader) mot basen.
- För kvadrater och rektanglar är höjden lika med längden på en vertikal sida, eftersom dessa sidor är i rät vinkel mot marken.

2. Jämför trianglar och parallellogram. Det finns ett enkelt förhållande mellan dessa två former. Att skära ett parallellogram på mitten längs diagonalen delar det i två lika trianglar. På samma sätt kan du sammanfoga två identiska trianglar för att bilda ett parallellogram. Det betyder att arean av en triangel kan skrivas som A = bh, exakt hälften så stor som ett motsvarande parallellogram.

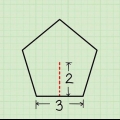
3. Hitta basen för den likbenta triangeln. Nu har du formeln, men exakt vad är "basen" och "höjden" av en likbent triangel? Basen är den enkla delen: ta bara den tredje, ojämna sidan av den likbenta triangeln.

4. Dra en linje mellan basen och den motsatta vertexen. Se till att linjen vidrör basen i rät vinkel. Längden på denna linje är triangelns höjd och är därför märkt h. När du får värdet av h beräknat kan du bestämma området.

5. Se ena halvan av den likbenta triangeln. Observera att höjden delar den likbenta triangeln i två identiska rätvinkliga trianglar. Titta på en av dem och peka på de tre sidorna:
 .
.
6.Använd Pythagoras sats. Om du känner till två sidor av en rätvinklig triangel och vill hitta den tredje kan du använda Pythagoras sats: (sida 1) + (sida 2) = (hypotenusa) Byt ut variablerna vi använder i denna uppgift och du får  .
.
 .
. . Genom att skriva detta som "sidor" och "hypotenusa" förhindrar du att du förväxlar dessa med variablerna i triangeln.
. Genom att skriva detta som "sidor" och "hypotenusa" förhindrar du att du förväxlar dessa med variablerna i triangeln.
7. Lösa åt h. Kom ihåg att du har areaformeln b och h används, men som du inte vet värdet av h vet inte än. Skriv om formeln h att lösa:


 .
.
8. Byt ut värdena på din triangel mot h Nu när du känner till den här formeln kan du använda den för en likbent triangel vars sidor du känner till. Ange bara längden på basen för b och längden på en av de lika sidorna för s, och räkna ut efteråt h.





 centimeter.
centimeter.
9. Använd bas- och höjdvärdena i areaformeln. Nu har du vad du behöver för att använda formeln från början av detta avsnitt: Area = ½bh. Byt ut värdena för b och h i denna formel och beräkna svaret. Glöm inte att skriva ditt svar i kvadratiska enheter.
A = ½(6cm)(4cm)
A = 12 cm.

10. Försök med ett svårare exempel. De flesta likbenta trianglar är svårare att arbeta med än i föregående exempel. Höjd innehåller ofta en kvadratrot som inte kan förenklas till ett heltal. Om så är fallet, lämna höjden som kvadratroten i enklaste formen att stå. Här är ett exempel:







Metod 2 av 2: Använda trigonometri

1. Börja med en sida och ett hörn. Om du är bekant med trigonometri kan du hitta arean av en likbent triangel även om ingen av längderna på dess sidor är kända. Här är ett exempel på problem där endast följande är känt:
- Längden s av de två lika sidorna är 10 cm.
- Vinkeln mellan de två lika sidorna är 120 grader.

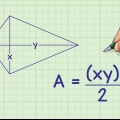
2. Dela den likbenta triangeln i två räta trianglar. Rita en linje ner från spetsen mellan de två lika sidorna, som skär basen i rät vinkel. Du har nu två lika räta trianglar.

3. Använd trigonometri för att bestämma värdet på h. Nu när du har en rätvinklig triangel kan du använda de trigonometriska funktionerna (sinus, cosinus och tangens). I exempelproblemet vet du vad hypotenusan är och du vill ha värdet på h vet, sidan bredvid den kända vinkeln. Använd det faktum att cosinus = angränsande / hypotenusa till h att lösa:

4. Bestäm värdet på den återstående sidan. Det finns en ännu okänd sida av den räta triangeln, som du X kan namnge. Lös detta med definitionen sinus = motsatt / hypotenusa:

5. Använd relationen mellan x och basen av den likbenta triangeln. Du kan nu "zooma ut" till den likbenta triangeln i fråga. Basen b av den vinkeln är lika med 2X, eftersom det var uppdelat i två segment, var och en med en längd X.

6. Använd värdena h och b i areaformeln för triangeln. Nu när du vet basen och höjden kan du använda standardformeln A = ½bh:





7. Skriv om detta som en universell formel. Nu när du vet hur du fixar detta kan du tillämpa den allmänna formeln utan att gå igenom hela processen varje gång. Här är vad du får om du upprepar den här processen, utan att använda specifika värden (och förenkla med hjälp av trigonometriegenskaperna):

Tips
- Om du har att göra med en likbent rätvinklig triangel (två lika sidor och en vinkel på 90 grader) är det mycket lättare att hitta arean. Om du använder en av kortsidorna som bas är den andra kortsidan höjden. Nu kan formeln A = ½ b * h förenklas till ½s, där s är längden på en kortsida.
- Kvadratrötter har två lösningar, en positiv och en negativ, men du kan ignorera den negativa i geometrin. Till exempel kan du inte ha en triangel med en "negativ höjd".
- Vissa trigonometriska problem ger dig annan information att börja med, som längden på basen och en vinkel (och det faktum att triangeln är likbent). Den grundläggande strategin förblir densamma: dela upp den likbenta triangeln i räta trianglar och räkna ut dem för höjden med hjälp av trigonometriska funktioner.
"Beräkna arean av en likbent triangel"
Оцените, пожалуйста статью