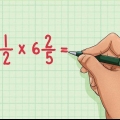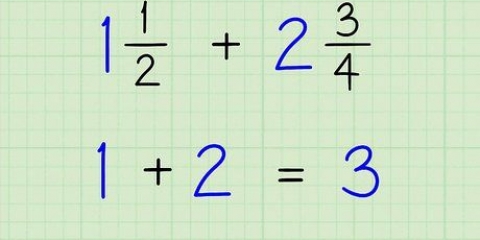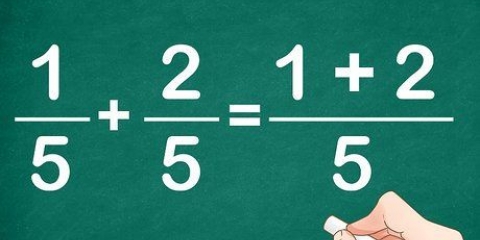I vårt exempel skulle vi utelämna resten och bara 1 skriv ner det (eftersom vårt svar är 1 R2). 
I vårt exempel är resten lika med 2. Om vi sätter detta som en täljare ovanför den ursprungliga nämnaren (5), får vi 2/5. Vi sätter detta bredvid vårt svar på hela talet (1) och får det slutliga blandade talet. Som följer: 1 2/5. 
Om vi vill göra en oegentlig bråkdel från svaret på vårt exempel (1 2/5), kan vi göra det så här: 1 × 5 = 5 → (2 + 5)/5 = 7/5 

99/5 — hur många gånger går 5 till 99? Eftersom 5 går exakt 20 gånger på 100, kan du anta att 5 går 19 gånger på 99. 99 ÷ 5 = 19 R 4 — nu skapar vi bara det blandade talet som tidigare. 99/5 = 19 4/5 
6/6 — sex går en gång i sex, utan vila, förstås. 6 6 = 1 R0. Eftersom ett bråktal med 0 i täljaren alltid är lika med noll, behöver vi inte sätta ett bråktal bredvid vårt heltal. 6/6 = 1 
18/6 — eftersom vi vet att 18 bara är 6 × 3, vet vi att vi kommer att ha en återstod av 0, så vi behöver inte oroa oss för bråkdelen av vårt blandade tal. 18/6 = 3 
-10/3 -10 ÷ 3 = -3 R1 -10/3 = -3 1/3
Konvertera oegentliga bråk till blandade tal
I matematik är oegentliga bråk de där täljaren (det översta talet) är större än eller lika med nämnaren (det nedersta talet). Att konvertera ett oegentligt bråktal till ett blandat tal (med ett bråktal och ett heltal, till exempel 2 3/4), dividera täljaren med nämnaren. Skriv hela delen av svaret bredvid ett bråk, med resten i täljaren och den ursprungliga nämnaren nedan - du har nu ett blandat bråk!
Steg
Metod 1 av 2: Konvertera en oegentlig bråkdel

1. Dividera täljaren med nämnaren. Börja skriva ner din felaktiga bråkdel. Dela sedan täljaren med nämnaren — med andra ord, räkna ut divisionssumman enligt bilden. Glöm inte att skriva ner resten.
- Låt oss ta ett exempel. Låt oss säga att vi måste omvandla bråktalet 7/5 till ett blandat tal. Vi delar först 7 med 5, till exempel:
- 7/5 → 7 ÷ 5 = 1 R2

2. Skriv hela talet för svaret. Hela talet för ditt blandade tal (det stora talet till vänster om ditt bråk) är svaret på hela talet för divisionssumman. Med andra ord, skriv bara divisionssvaret utan resten.

3. Gör en bråkdel av resten och den ursprungliga nämnaren. Nu måste vi hitta bråkdelen av det blandade talet. Lägg in resten av divisionen i täljaren och använd samma nämnare för ditt ursprungliga oegentliga bråk. Sätt denna bråkdel bredvid ditt hela tal och du har ditt blandade tal!

4. För att göra detta till ett oegentligt bråk igen lägger vi till hela talet till täljaren. Blandade siffror ser bra ut på papper och är lätta att läsa, men är inte alltid det bästa valet. Till exempel, om vi multiplicerar ett bråktal och ett blandat tal, blir vårt jobb mycket lättare om vi konverterar det blandade talet tillbaka till ett oegentligt bråktal. Det gör du genom att helt enkelt multiplicera hela talet med nämnaren och lägga till täljaren.
Metod 2 av 2: Lösa provproblem

1. Konvertera 11/4 till ett blandat tal. Det här problemet är enkelt - lös det bara precis som ovan. Se nedan för en steg-för-steg-lösning.
- 11/4 — till att börja med måste vi dividera täljaren med nämnaren.
- 11 ÷ 4 = 2 R 3 — nu måste vi göra en bråkdel av resten och vår ursprungliga nämnare.
- 11/4 = 2 3/4

2. Konvertera 99/5 till ett blandat tal. Vi har att göra med en mycket stor disk här, men låt det inte lura dig - metoden är exakt densamma! Se nedan:

3. Konvertera 6/6 till ett blandat tal. Hittills har vi bara behandlat oegentliga bråk där täljaren är större än nämnaren. Men vad händer när båda är likadana? Se nedan för att ta reda på det.

4. Konvertera 18/6 till ett blandat tal. Om täljaren är en multipel av nämnaren, oroa dig inte för resten - gör bara divisionssumman för att få ditt svar. Se nedan.

5. Konvertera -10/3 till ett blandat tal. Negativ fungerar precis som positiva tal. Se nedan:
Tips
- Felaktiga bråk är inte nödvändigtvis fel. Faktum är att de ibland är mer användbara än blandade siffror. Om du till exempel ska multiplicera två bråk, är oegentliga bråk bättre eftersom du bara måste multiplicera täljarna och nämnarna för att få ditt svar: t.ex. 1/6 × 7/2 = 7/12. Multiplicera nu 1/6 × 3 1/2 — inte riktigt lätt.
- Å andra sidan är blandade siffror oftast mest användbara när man ska beskriva något i verkligheten. Till exempel kräver ett recept 4 1/2 koppar mjöl, inte 9/2 koppar mjöl.
"Konvertera oegentliga bråk till blandade tal"
Оцените, пожалуйста статью