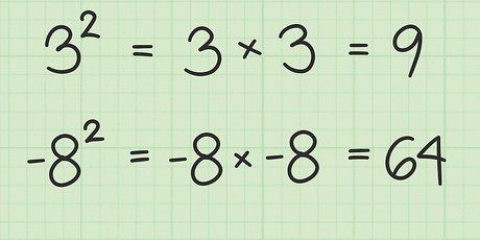Förenkla kvadratrötter
Att förenkla en kvadratrot är inte så svårt som det verkar. För att förenkla en kvadratrot behöver du bara faktorisera kvadratrotens tal och försöka ta kvadratroten av en eller båda faktorerna. När du väl känner till några vanliga kvadrattal och vet hur man delar ett tal i faktorer är du på god väg att förenkla en kvadratrot. Så här kan du lära dig detta snabbt.
Steg
Metod 1 av 4: Förenkla kvadratroten av ett tal

1. Lär dig några kvadrattal och deras rötter. Att kvadrera, multiplicera ett tal med sig själv, blir ett kvadratiskt tal (perfekt kvadrat). Till exempel: 25 är ett tal i kvadrat eftersom 5 x 5, eller 5, är lika med 25. Att känna till åtminstone de första 10 tio kvadrattalen kan hjälpa till att känna igen och förenkla kvadratrötter. Här är de första tio kvadratiska talen:
- 1 = 1
- 2 = 4
- 3 = 9
- 4 = 16
- 5 = 25
- 6 = 36
- 7 = 49
- 8 = 64
- 9 = 81
- 10 = 100

2. Hitta kvadratroten ur ett kvadrattal. Om du ser ett kvadrattal under en radikal, behöver du bara ta bort radikalen (√ ), och skriva kvadratroten av kvadrattalet. Om du redan hade lärt dig detta utantill, då är du klar. Om talet är för stort och du inte är säker på om det är ett kvadrattal, försök hitta kvadratroten med din miniräknare för att kontrollera om det ger ett fint runt tal. Till exempel: vid √25 vet du att svaret är lika med 5 eftersom 25 är ett tal i kvadrat.
Metod 2 av 4: Förenkla en kvadratrot genom att faktorisera

1. Om talet är jämnt, dividera det med 2. Att hitta faktorerna för ett tal innebär att hitta alla tal som multiplicerat tillsammans ger det talet, vilket gör det lättare att bestämma dess kvadratrot. Om det är ett jämnt tal är det första du kan göra att dividera talet med 2. I det här exemplet kan du dela √98 i √(2x49), eftersom 98 : 2 =49. Om talet inte är delbart med 2, prova 3, 4, 5, och så vidare, tills du hittar rätt kombination.

2. Dela tillbaka dessa faktorer i faktorer för att hitta ytterligare kvadrattal. Se om du kan fortsätta dela upp antalet i faktorer. 2 är primtal och har bara sig själv och 1 som divisor. Men 49, den andra faktorn, kan fortfarande delas in i 7 x 7, eftersom det är ett kvadrattal. Så du kan skriva om roten √(2x49) som √(2x7x7), eller √[2(7)], vilket betyder att vi redan har hittat kvadrattalet vi letade efter.

3. Förenkla kvadratroten. Eftersom √98= √[2(7)] är det möjligt att placera en 7:a utanför radikalen och förenkla svaret till 7√2. Så √49 eller också (7 x 7), blir sedan 7 så snart du placerar den utanför radikalen. Om du placerar tillbaka 7:an igen blir det ett kvadrattal igen och därför 49. Så, √98 = 7√2.
Metod 3 av 4: Andra metoder för att förenkla en kvadratrot
1. Om du inte omedelbart lyckas hitta ett kvadrattal, dividera sedan talet ytterligare. Till exempel, om problemet är √48, fortsätter du dividera tills du inte kan gå längre än 2x2, så att 4 blir en koefficient för radikalen och 3 förblir inuti radikalen. Så här fungerar det:
- √48 = √(2 x 24)
- √(2 x 24) = √(2 x 12 x 2)
- √(2 x 12 x 2) = √(2 x 6 x 2 x 2)
- √(2 x 6 x 2 x 2) = √(2 x 3 x 2 x 2 x 2)
- √(2 x 3 x 2 x 2 x 2) = √(2 x 3)
- √(2 x 3)= 4√3
- √48 = 4√3
2. Kom ihåg att du inte kan förenkla ett primtal. Det beror på att faktorerna här är 1 och själva primtalet. Till exempel: √17 kan inte förenklas eftersom 17 är primtal.
3. Dela upp i faktorer med mer än ett kvadrattal. Om talets faktorer innehåller mer än ett kvadrattal, ta dem alla utanför radikalen. Om du har hittat flera rutor medan du förenklar, ta alla utanför radikalen och multiplicera dem. Till exempel: Låt oss anta att du vill förenkla talet √32 och dela det sedan i faktorerna 4 x 4 x 2, och notera att kvadrattalet 4 förekommer två gånger. Gör denna 16√2 som så småningom kommer att ge 4√2.
4. Blanda inte ihop koefficienten med en högre kraftrot. 3√125, till exempel, är lika med 3 x √125, men √125 är kubroten av 125. (eftersom 5 x 5 x 5 = 125, √125 = 5.)
Metod 4 av 4: Att känna till terminologin

1. Kom ihåg att radikalen (√) är symbolen för kvadratroten. Till exempel, i problemet √25, "√" det radikala tecknet.

2. Kom ihåg att radikalen är siffran under radikalen. Hitta kvadratroten av detta tal. Till exempel: vid √25 är "25" rotnumret.

3. Kom ihåg att koefficienten är talet utanför radikalen. Detta tal multiplicerar kvadratroten; Detta kan hittas till vänster om det radikala tecknet, √-symbolen. Till exempel: vid 7√2, "7" koefficienten.

4. Kom ihåg att en faktor är ett tal som går helt in i ett annat tal. Till exempel: 2 är en faktor på 8 eftersom 8 ÷ 4 = 2, men 3 är inte en faktor på 8 eftersom 8÷3 inte svarar på ett heltal. Till exempel: 5 är en faktor på 25 eftersom 5 x 5 = 25.

5. Förstå innebörden av att förenkla en kvadratrot. Att förenkla en kvadratrot innebär helt enkelt att dela upp en kvadrat av en kvadratrot i faktorer, sedan flytta den till vänster om radikalen och lämna den andra faktorn inuti radikalen. Om talet är ett kvadrattal så kan du ta bort det radikala tecknet så snart du har skrivit dess kvadratrot. Till exempel: √98 kan förenklas till 7√2.
Tips
- Ett sätt att hitta rutor för att dividera dina kvadratiska tal är att slå upp rutor i din lista som börjar med det minsta talet efter ditt kvadratiska tal. Till exempel: om du letar efter kvadrattalet 27, börja vid 25 och sluta vid 9, eftersom du har hittat den största divisorn som är ett kvadrattal.
Varningar
- Använd inte miniräknare förutom i steget där du försöker räkna ut hur många gånger kvadraten går in i kvadratroten.
- Att förenkla är inte detsamma som att sätta värden i en ekvation.Ingenstans i hela processen kan ett decimaltal förekomma någonstans!
"Förenkla kvadratrötter"
Оцените, пожалуйста статью