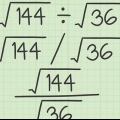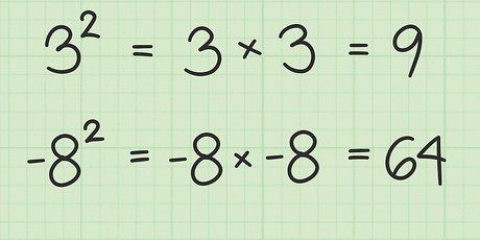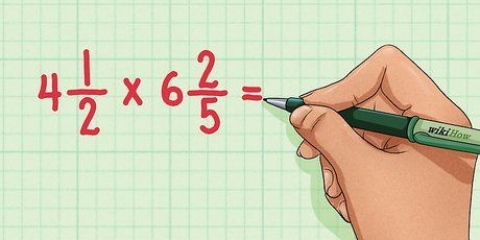En perfekt kvadrat är resultatet av att multiplicera ett tal (positivt eller negativt heltal) med sig själv. Till exempel: 25 är en perfekt kvadrat eftersom  .
. Till exempel,  kan räknas in i den perfekta kvadraten 25:
kan räknas in i den perfekta kvadraten 25:

=

Till exempel,  kan lösas upp i
kan lösas upp i  , för kvadratroten ur 25 (vilket är 5):
, för kvadratroten ur 25 (vilket är 5):

=
=

Till exempel,  . Du får det här resultatet pga
. Du får det här resultatet pga  .
. 

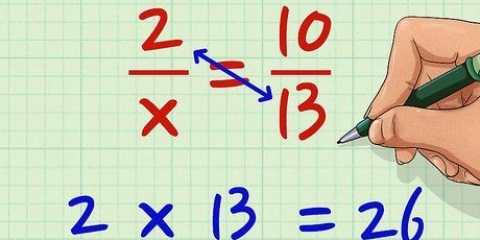
Till exempel för ett uttalande som  , beräkna produkten av siffrorna under radikalerna med hjälp av
, beräkna produkten av siffrorna under radikalerna med hjälp av  , så att
, så att  . Uppgiften ser nu ut så här:
. Uppgiften ser nu ut så här:  .
. 
En kvadrat är resultatet av att multiplicera ett heltal (positivt eller negativt) med sig själv. Till exempel: 4 är en kvadrat, eftersom  .
. Till exempel:  kan faktoriseras så att kvadraten på 4 placeras före radikalen:
kan faktoriseras så att kvadraten på 4 placeras före radikalen:

=

Till exempel,  kan lösas upp i
kan lösas upp i  , varefter du kan ta kvadratroten ur 4 (det vill säga 2) varefter du multiplicerar detta med 6:
, varefter du kan ta kvadratroten ur 4 (det vill säga 2) varefter du multiplicerar detta med 6:

=
=
=
Multiplicera kvadratrötter
Precis som att multiplicera heltal kan du också multiplicera kvadratrötter (en kvadratrotsekvation) tillsammans. Ibland har kvadratrötter koefficienter (ett heltal före radikalen), men detta lägger bara till ett steg till multiplikationen och ändrar inte processen. Den svåraste delen av kvadratrotsmultiplikation är att förenkla uttrycket för att få det slutgiltiga svaret, men även det här steget är enkelt om du kan dina perfekta kvadrater.
Steg
Metod 1 av 2: Multiplicera kvadratrötter utan koefficienter

1. Multiplicera rötterna tillsammans. En radicand (engelska) är ett tal under radikalen. Multiplicera rötter på samma sätt som heltal. Se till att produkten förblir under det radikala tecknet.
- Till exempel om du räknar
, då får du
. så,
.

2. Härled alla perfekta kvadrater från kvadratroten. Det gör du genom att kontrollera om en perfekt kvadrat är en faktor av talet under radikalen. Om du inte kan härleda en perfekt kvadrat, har ditt svar redan förenklats och du behöver inte göra något annat.
 .
. kan räknas in i den perfekta kvadraten 25:
kan räknas in i den perfekta kvadraten 25:
=


3. Placera kvadratroten före radikalen. Lämna den andra faktorn under radikalen. Nu har du det förenklade uttrycket.
 kan lösas upp i
kan lösas upp i  , för kvadratroten ur 25 (vilket är 5):
, för kvadratroten ur 25 (vilket är 5):
=

=


4. Beräkna kvadraten av en kvadratrot. I vissa fall måste du multiplicera en kvadratrot med sig själv. Att kvadrera ett tal och ta kvadratroten ur ett tal är motsatta operationer; så de gör upp varandra. Resultatet av kvadraten av en kvadratrot är helt enkelt talet under radikalen.
 . Du får det här resultatet pga
. Du får det här resultatet pga  .
.Metod 2 av 2: Multiplicera kvadratrötter med koefficienter

1. Multiplicera koefficienterna. En koefficient är ett tal för radikalen. Ignorera bara radikalen och talet under den och multiplicera de två heltalen tillsammans. Placera sin produkt före den första radikalen.
- Se upp för plus- och minustecken när du multiplicerar koefficienter. Kom ihåg att ett negativt tal gånger ett positivt tal ger ett negativt resultat och ett negativt tal gånger ett negativt tal ger ett positivt resultat.
- Till exempel vid beräkning
, räkna först
. Nu är uppgiften följande:
.

2. Multiplicera siffrorna under radikalerna. För att göra detta, multiplicera talen som om de vore heltal. Se till att produkten håller sig under det radikala tecknet.
 , beräkna produkten av siffrorna under radikalerna med hjälp av
, beräkna produkten av siffrorna under radikalerna med hjälp av  , så att
, så att  . Uppgiften ser nu ut så här:
. Uppgiften ser nu ut så här:  .
.
3. Om möjligt, faktor ut alla rutor under det radikala tecknet. Du måste göra detta för att förenkla ditt svar. Om du inte kan lösa en kvadrat har ditt svar redan förenklats och du kan hoppa över det här steget.
 .
. kan faktoriseras så att kvadraten på 4 placeras före radikalen:
kan faktoriseras så att kvadraten på 4 placeras före radikalen:
=


4. Multiplicera roten av kvadraten med koefficienten. Lämna den andra faktorn under radikalen. Detta ger ett förenklat uttryck.
 kan lösas upp i
kan lösas upp i  , varefter du kan ta kvadratroten ur 4 (det vill säga 2) varefter du multiplicerar detta med 6:
, varefter du kan ta kvadratroten ur 4 (det vill säga 2) varefter du multiplicerar detta med 6:
=

=

=

Tips
- Känn dina rutor, för det gör den här processen mycket lättare!
- Följ de vanliga reglerna för tecknet för ett tal för att avgöra om den nya koefficienten kommer att vara positiv eller negativ. En positiv koefficient multiplicerad med en negativ koefficient ger ett negativt tal. Två positiva koefficienter multiplicerade tillsammans eller två negativa koefficienter multiplicerade tillsammans ger ett positivt tal.
- Alla termer under radikalen är alltid positiva, så du behöver inte oroa dig för tecknet när du multiplicerar tal under en radikal.
Förnödenheter
- Penna
- Papper
- Kalkylator
"Multiplicera kvadratrötter"
Оцените, пожалуйста статью