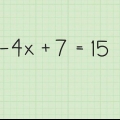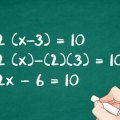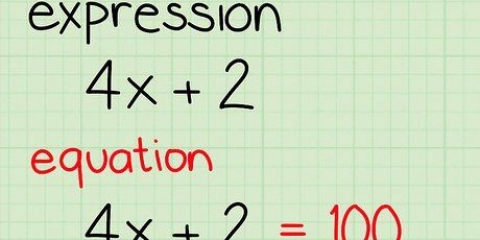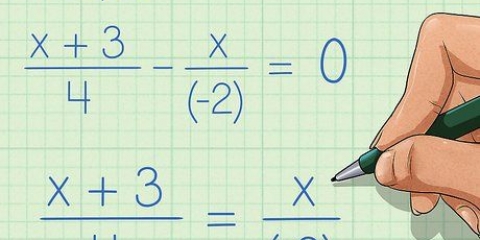4(x+3) + 9 - 5 = 32 
4x + 12 + 9 - 5 = 32 
4x+21-5 = 32 4x+16 = 32 4x + 16 - 16 = 32 - 16 4x = 16 
4x/4 = 16/4 x = 4 
2(x+3)+ 9 - 5 = 32 2(4+3)+ 9 - 5 = 32 2(7) + 9 - 5 = 32 4(7) + 9 - 5 = 32 28 + 9 - 5 = 32 37 - 5 = 32 32 = 32 

2x+12-12 = 44-12 2x = 32 
(2x)/2 = 32/2 x = 16 

2x + 12 = 44 2 x (4) + 12 = 44 2 x 16 + 12 = 44 32 + 12 = 44 44 = 44 

(x + 3)/6 = 2/3 6 x 2 = 12 (x + 3) x 3 = 3x + 9 3x + 9 = 12 
3x + 9 - 9 = 12 - 9 3x = 3 

(x + 3)/6 = 2/3 (1 + 3)/6 = 2/3 4/6 = 2/3 2/3 = 2/3 

√(2x+9) - 5 + 5 = 0 + 5 √(2x+9) = 5 
(√(2x+9)) = 5 2x + 9 = 25 
2x + 9 - 9 = 25 - 9 2x = 16 

√(2x+9) - 5 = 0 √(2(8)+9) - 5 = 0 √(16+9) - 5 = 0 √(25) - 5 = 0 5 - 5 = 0 

|4x +2| - 6 = 8 |4x +2| - 6 + 6 = 8 + 6 |4x +2| = 14 
4x + 2 = 14 4x + 2 - 2 = 14 -2 4x = 12 x = 3 
4x + 2 = -14 4x + 2 - 2 = -14 - 2 4x = -16 4x/4 = -16/4 x = -4 
(För x = 3): |4x +2| - 6 = 8 |4(3) +2| - 6 = 8 |12 +2| - 6 = 8 |14| - 6 = 8 14 - 6 = 8 8 = 8 (för x = -4): |4x +2| - 6 = 8 |4(-4) +2| - 6 = 8 |-16 +2| - 6 = 8 |-14| - 6 = 8 14 - 6 = 8 8 = 8
Lös x i en ekvation
Det finns flera sätt att lösa x i en ekvation, oavsett om du arbetar med exponenter och rötter eller helt enkelt behöver dividera eller multiplicera. Vilken metod du än använder, bör du alltid hitta ett sätt att isolera x från ena sidan av ekvationen så att du kan beräkna värdet. Så här gör du det:
Steg
Metod 1 av 5: Använda en vanlig linjär ekvation

1. Skriv ner problemet. Här är uppdraget:
- 2(x+3) + 9 - 5 = 32

2. Räkna ut exponenten. Kom ihåg operationsordningen: HMVDOA, som står för Parentheses, Exponentiation, Division/Multiply, Addition/Subtraction. I det här fallet kan du inte räkna ut vad som står inom parentes först eftersom x tillhör det, så du börjar med potensen 2. 2 = 4

3. Räkna ut multiplikationen. Multiplicera 4 med (x+3). Här är hur:

4. Räkna nu ut addition och subtraktion. Lägg bara till eller subtrahera de återstående siffrorna. Här är hur:

5. Isolera variabeln. Du gör detta genom att dividera båda sidor av ekvationen med 4 för att hitta x. 4x/4 = x och 16/4 = 4, alltså x = 4.

6. Kontrollera din beräkning. Sätt tillbaka x = 4 i den ursprungliga ekvationen för att se till att den är korrekt. Här är hur:
Metod 2 av 5: Med exponentiering

1. Skriv ner problemet. Låt oss anta att du arbetar med ett problem där x-termen också innehåller en exponent:
- 2x + 12 = 44

2. Isolera termen med exponenten. Det första du bör göra nu är att kombinera lika termer så att alla konstanter är på höger sida av ekvationen, medan termen med exponenten är till vänster. Subtrahera bara 12 från båda sidor. Här är hur:

3. Isolera variabeln med exponenten genom att dividera båda sidor med koefficienten för x-termen. I det här fallet är 2 x-koefficienten, vilket betyder att båda sidorna måste delas med 2 för att eliminera den. Här är hur:

4. Ta kvadratroten av varje sida av ekvationen. Genom att beräkna kvadratroten ur x får du x till vänster och kvadratroten ur 16,4 till höger. Alltså, x = 4.

5. Kontrollera din beräkning. Sätt tillbaka x = 4 i den ursprungliga ekvationen för att se till att den är korrekt. Här är hur:
Metod 3 av 5: Använd bråk

1. Skriv ner problemet. Låt oss anta att du har att göra med följande problem:
- (x + 3)/6 = 2/3

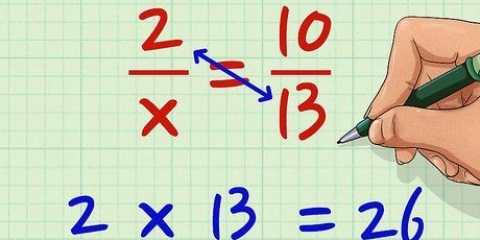
2. Cross Multiplicera. För att multiplicera korsvis, multiplicera nämnaren för varje bråkdel gånger täljaren för det andra bråket. Så, multiplicera 6 (den första nämnaren) med 2 (den andra täljaren), för att få 12 på höger sida av ekvationen.Multiplicera sedan 3 (den andra nämnaren) med x + 3 (den första täljaren), för att få 3 x + 9 till vänster om ekvationen. Så här kommer det att se ut:

3. Kombinera liknande termer. Kombinera konstanterna i ekvationen genom att subtrahera 9 från båda sidor av ekvationen. Så här gör du:

4. Isolera x genom att dividera varje term med x-koefficienten. Dela bara 3x och 9 med 3, koefficienten för x, och lös x. 3x/3 = x och 3/3 = 1, så du står kvar med x = 1.

5. Kontrollera din beräkning. För att kontrollera ditt arbete, sätt tillbaka x i den ursprungliga ekvationen för att se till att det är korrekt. Så här gör du:
Metod 4 av 5: Använda rottecken

1. Skriv ner problemet. Låt oss anta att du löser x i följande problem:
- √(2x+9) - 5 = 0

2. Isolera kvadratroten. Du måste isolera kvadratrotdelen av ekvationen till vänster om ekvationen innan du kan fortsätta. Så du lägger till 5 på båda sidor av ekvationen. Här är hur:

3. Rita kvadratroten på båda sidorna. Precis som du dividerar båda sidorna av en ekvation med koefficienten multiplicerad med x, måste du också ta kvadratroten av båda sidorna av en ekvation om x är under radikaltecknet. Detta tar bort radikalen från ekvationen. Så här gör du:

4. Kombinera liknande termer. Kombinera lika termer genom att subtrahera 9 från båda sidor av ekvationen så att alla konstanter är till höger, medan x förblir till vänster. Så här gör du:

5. Isolera variabeln. Det sista du kan göra för att lösa för x är att isolera variabeln genom att dividera båda sidor av ekvationen med 2, koefficienten för x-termen. 2x/2 = x och 16/2 = 8, så du står kvar med x = 8.

6. Kontrollera din beräkning. Skriv in 8 i ekvationen igen för x för att kontrollera att din beräkning är korrekt:
Metod 5 av 5: Använd det absoluta värdet

1. Skriv ner problemet. Låt oss anta att du försöker lösa x i följande problem:
- |4x +2| - 6 = 8

2. Isolera det absoluta värdet. Det första du ska göra är att kombinera liknande termer och isolera det absoluta värdet. I det här fallet kan du göra det genom att lägga till 6 på båda sidor av ekvationen. Här är hur:

3. Ta bort det absoluta värdet och lös ekvationen. Detta är det första och enklaste steget. Du måste nu lösa x två gånger, varje gång du arbetar med ett absolut värde. Så här gör du första gången:

4. Ta bort det absoluta värdet och ändra tecknet för termerna på andra sidan likhetstecknet innan du fortsätter att lösa. Gör nu detta igen, denna gång gör den vänstra delen av ekvationen lika med -14 istället för 14. Här är hur:

5. Kontrollera din beräkning. Nu när du vet att x = (3, -4), sätt bara tillbaka båda talen i ekvationen för att se till att det är rätt. Här är hur:
Tips
- För att kontrollera ditt arbete, skriv in värdet på x tillbaka i den ursprungliga ekvationen och lös för det.
- Rötter är ett annat sätt att representera exponenter.Kvadratroten ur x = x^1/2.
Оцените, пожалуйста статью