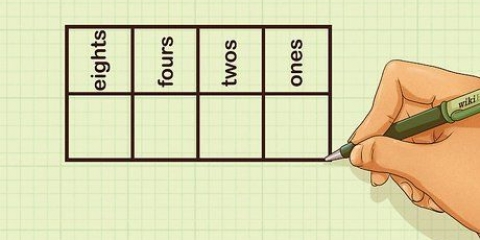
11 > 1, alltså 11 "passar inte" 1. Skriv en 0 som den första siffran i kvoten (ovanför den första siffran i utdelningen). 
Ta ner nästa siffra i utdelningen. 11 > 10. Skriv en 0 i kvoten. Ta ner nästa nummer. 11 < 101. Skriv en 1:a i kvoten. 
Skriv divisorn under utdelningen. Här skriver vi detta som 11 under de tre första siffrorna (101) i utdelningen. Beräkna 101 - 11 för resten, 10. Se över hur du subtraherar binära tal om du inte kommer ihåg. 
Skriv 11 under 100 och subtrahera dessa siffror för att få 1. Ta ner sista siffran i utdelningen så får du 11 som svar. 11 = 11, så du skriver 1 som den sista siffran i kvoten (svaret). Det finns ingen rest, så uppgiften är klar. Svaret är 00111, eller enklare, 111. 
Att dividera binära tal resulterar ofta i att tal upprepas efter decimalkomma, oftare än de som förekommer med decimalnotation. Detta hänvisas till med den mer allmänna termen "radixpunkt" som du stöter på i valfritt talsystem, eftersom du har "decimalpunkt" endast påträffas inom decimalsystemet. 

Hitta komplementet till ettorna i den andra termen, subtrahera varje siffra från 1. Du kan enkelt göra detta med binära tal genom att ställa in var 1 till 0 och var 0 till 1. I vårt exempel är 011 lika med 100. Lägg till 1 till resultatet: 100 + 1 = 101. Detta kallas 2:ans komplement. Vi ska nu betrakta en minussumma som en tilläggssumma. Kärnan är att vi betraktar problemet som om vi adderar ett negativt tal istället för att subtrahera ett positivt tal, efter att ha slutfört proceduren. Lägg till resultatet till den första termen. Lös summan: 111 + 101 = 1100. Utelämna den första siffran (bär siffran). Ta bort den första siffran från ditt svar för att få det slutliga resultatet. 1100 → 100. 

2:s komplement av 000101 = 111010 + 1 = 111011 100011 + 111011 = 1011110 Utelämna den första siffran (bäraren) → 011110 

011110 + 111011 = 1011001 → 011001 (kvotient 1+1=10) 011001 + 111011 = 1010100 → 010100 (kvotient 10+1=11) 010100 + 111011 = 1001111 → 001111 (11+1=100) 001111 + 111011 = 1001010 → 001010 (100+1=101) 001010 + 111011 = 10000101 → 0000101 (101+1=110) 0000101 + 111011 = 1000000 → 000000 (110+1=111) 0 är mindre än 101, så vi kan sluta nu. Kvoten 111 är svaret på delproblemet. Resten är det slutliga resultatet av vår minsumma, i detta fall 0 (ingen vila).
Dela binära tal
Att dividera binära tal kan lösas med långdivision, en bekväm metod för att lära dig själv proceduren eller skriva ett enkelt datorprogram. Alternativt erbjuder komplementmetoden med upprepad subtraktion ett tillvägagångssätt som du kanske inte är bekant med, även om det inte riktigt används i programmering. Maskinspråk använder vanligtvis en uppskattningsalgoritm för större effektivitet, men dessa beskrivs inte här.
Steg
Metod 1 av 2: Använd lång division

1. Gå över decimal lång division igen. Om det var ett tag sedan du gjorde lång division med vanliga decimaltal (bas 10), se över dess bas för problemet 172 ÷ 4. I annat fall, hoppa över detta och gå till nästa steg för att lära dig denna procedur för binära tal.
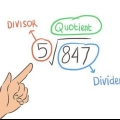
- Det utdelning delas med divisor, och svaret är det kvot.
- Jämför divisorn med den första siffran i utdelningen. Om divisorn är det största talet, fortsätt att lägga till siffror till utdelningen tills divisorn är det minsta talet. (Som ett exempel, när vi beräknar 172 ÷ 4, jämför vi 4 och 1, finner vi att 4 > 1 och jämför sedan 4 med 17.)
- Skriv den första siffran i kvoten ovanför den sista siffran i den utdelning som används för jämförelse. Efter att ha jämfört 4 och 17, noterar vi att 4 går in i 17 fyra gånger, så vi skriver 4 som den första siffran i vår kvot, över 7.
- Multiplicera och subtrahera för att hitta resten. Multiplicera kvoten med divisor, i det här fallet 4 x 4 = 16. Skriv 16 under 17 och gör sedan 17 - 16 för resten, 1.
- Upprepa. Återigen jämför vi divisorn 4 med nästa siffra, 1, vi märker att 4 > 1, och "föra" vi flyttar nästa siffra i utdelningen ner för att jämföra 4 med 12 istället. 4 går in i 12 tre gånger utan rest, så vi kan skriva 3 som nästa siffra i kvoten. Svaret är 43.

2. Skapa en binär lång divisionsuppsättning. Anta att vi använder 10101 ÷ 11 som exempel. Skriv detta som lång division, med 10101 som utdelning och 11 som divisor. Lämna utrymme ovanför den för att skriva kvoten och skriv dina beräkningar under den.

3. Jämför divisorn med den första siffran i utdelningen. Detta fungerar på samma sätt som decimal lång division, men är faktiskt mycket lättare i binär form. Antingen kan du inte dividera talet med divisorn (0), eller så passar divisorn in en gång (1):

4. Ta nu nästa nummer och upprepa tills du får 1. Här är de kommande stegen från vårt exempel:

5. Bestäm resten. som i decimal lång division multiplicerar vi siffran vi just hittade (1) med divisorn (11) och skriver resultatet under vår utdelning på en rad med siffran vi just beräknade. I binär form kan vi göra detta snabbare, eftersom 1 x divisorn alltid är lika med divisorn:

6. Fortsätt tills problemet är löst. Ta med nästa siffra från återförsäljaren till resten nedan för att få 100. Eftersom 11 < 100 skriver du en 1:a som nästa siffra i kvoten. Fortsätt lösa problemet som tidigare:

7. Lägg till en radixpunkt om det behövs. Ibland är resultatet inte ett heltal. Om du fortfarande har en rest efter att ha använt den sista siffran, lägg till en ".0" till utdelningen och en "." till din kvot så att du kan få ner ytterligare ett nummer och gå vidare. Fortsätt göra detta tills du når önskad noggrannhet, avrunda sedan ditt svar. På papper kan du avrunda genom att utelämna nollan eller, om den sista siffran är en 1:a, subtrahera den och lägga till 1 till den sista siffran. Vid programmering, använd en av standardavrundningsalgoritmerna för att undvika fel vid konvertering mellan binära och decimala tal.
Metod 2 av 2: Använder komplementmetoden

1. Förstå grundidén. Ett sätt att lösa divisioner – för vilken bas som helst – är att fortsätta subtrahera divisorn från utdelningen och sedan resten, räkna ut hur många gånger du kan fortsätta göra detta innan du kommer till ett negativt tal. Här är ett exempel för basen 10, problemet 26 ÷ 7:
- 26 - 7 = 19 (1 gånger subtraherade)
- 19 - 7 = 12 (2 gånger subtraherade)
- 12 - 7 = 5 (3 gånger subtraherade)
- 5 - 7 = -2. Negativt tal, så upp igen. Svaret är 3 med en rest av 5. Observera att denna metod inte tar hänsyn till decimalsiffror.

2. Lär dig att subtrahera med hjälp av komplement. Även om du enkelt kan tillämpa ovanstående metod på binära tal, kan vi också använda en mer effektiv metod, vilket kan spara tid när du programmerar binära divisioner. Detta kallas den binära komplementmetoden. Här är grunderna, där vi beräknar 111 - 011 (se till att båda siffrorna är lika långa):

3. Kombinera de två begreppen ovan. Nu vet du hur subtraktionsmetoden för att lösa divisioner fungerar och 2-komplementmetoden för att lösa summan av minus. Du kan kombinera de två till en metod för att lösa divisionsproblem genom att använda stegen nedan. Om du vill kan du försöka ta reda på det själv innan du fortsätter.

4. Subtrahera divisorn från utdelningen genom att lägga till 2:ans komplement. Låt oss lösa följande problem: 100011 ÷ 000101. Det första steget är att lösa 100011 - 000101, med hjälp av 2-komplementmetoden, så att det blir en summa:

5. Lägg till 1 till kvoten. I ett datorprogram är det här du ökar kvoten med 1. På papper, gör en anteckning i ett hörn någonstans, där det inte kommer att förstöra resten av ditt arbete. Vi har nu framgångsrikt gjort en minsumma en gång, så kvoten hittills är 1.

6. Upprepa genom att subtrahera divisorn från resten. Resultatet av vår senaste beräkning är resten kvar efter divisorn en gång "gick in". Fortsätt att lägga till divisorns 2:a komplement och subtrahera carry. Lägg till 1 till kvoten varje gång och fortsätt tills du får en rest lika med din mindre divisor:
Tips
- Inkrementen för ökning, minskning eller stack bör övervägas innan en binär beräkning tillämpas på en uppsättning maskinsatser.
- 2:ans komplementmetod för subtraktion fungerar inte om talen består av ett annat antal siffror. Lägg till extra nollor till det mindre talet för att lösa detta.
- Ignorera den signerade siffran i signerade binära tal innan du gör beräkningen, förutom när du försöker ta reda på om ett svar är positivt eller negativt.
"Dela binära tal"
Оцените, пожалуйста статью