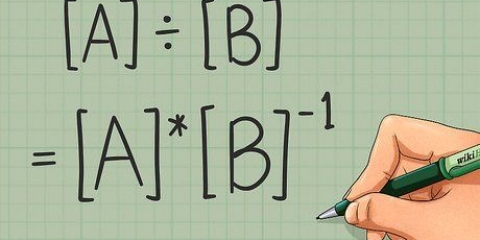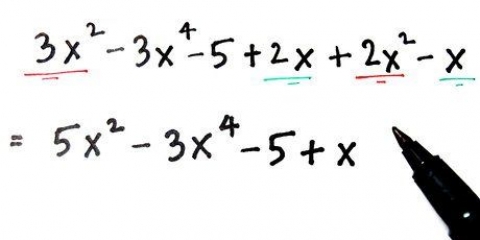-2| 1 2 -4 8
↓
1 
-2| 1 2 -4 8
-2
1 
-2| 1 2 -4 8
-2
10 
-2| 1 2 -4 8
-2 0
1 
-2| 1 2 -4 8
-2 0
10 -4 
-2| 1 2 -4 8
-2 0 8
1 0 -4 |16 
-2| 1 2 -4 8
-2 0 8
1 0 -4 |16
X + 0X - 4 R 16
X - 4R16 
Dela polynom syntetiskt
Syntetisk division är en förkortad metod för att dividera polynom där man delar polynomens koefficienter för att ta bort variabler och exponenter. Detta gör att du kan arbeta under denna beräkning på samma sätt som med vanlig långdivision. Om du vill veta hur man delar polynom syntetiskt, följ stegen nedan.
Steg

1. Skriv ner problemet. Till exempel dividerar du x + 2x - 4x + 8 med x + 2. Skriv den första andragradsekvationen, utdelningen, i täljaren och skriv den andra ekvationen, divisor, i nämnaren.

2. Vänd om tecknet för konstanten i divisorn. Konstanten i divisorn, x + 2, är positiv så inversen av konstantens tecken är -2.

3. Placera detta nummer utanför delen utanför delningstecknet. Delningstecknet ser ut som en baklänges"l." Placera termen -2 till vänster om denna symbol.

4. Skriv ner alla koefficienter för utdelningen inom divisionstecknet. Skriv termerna från vänster till höger när de visas. Det här ser ut så här: -2| 12-48.

5. Sänk den första koefficienten. Placera den första koefficienten, 1, under sig själv. Det här ser ut så här:
↓
1

6. Multiplicera den första koefficienten med divisorn och placera den under den andra koefficienten. Multiplicera 1 med -2 och skriv produkten -2 under den andra termen, 2. Det här ser ut så här:
-2
1

7. Lägg till den andra koefficienten och skriv svaret under produkten. Ta nu den andra koefficienten, 2, och lägg till den till -2. Du skriver resultatet 0 under de två talen, precis som med lång division. Så här ser det ut:
-2
10

8. Multiplicera summan med divisor och placera resultatet under den tredje koefficienten. Ta nu summan, 0, och multiplicera den med divisorn, -2. Placera resultatet 0 under 4, den tredje koefficienten. Så här ser det ut:
-2 0
1

9. Lägg ihop produkten och den tredje koefficienten och skriv resultatet under produkten. Lägg till 0 till -4 och skriv svaret -4 under 0. Så här ser det ut:
-2 0
10 -4

10. Multiplicera detta tal med divisor, skriv det under den sista koefficienten och lägg till det till koefficienten. Multiplicera nu -4 med -2 och skriv svaret 8 under den fjärde koefficienten, 8, och addera detta till den fjärde koefficienten. 8 + 8 = 16, så detta är din återstod. Skriv numret under produkten. Så här ser det ut:
-2 0 8
1 0 -4 |16

11. Placera var och en av de nya koefficienterna bredvid en variabel med en potens som är mindre än de ursprungliga variablerna. I det här fallet är den första summan 1 och placeras bredvid ett x höjt till andra potensen (1 mindre än 3). Den andra summan, 0, placeras bredvid ett x, men resultatet är 0, så denna term kan tas bort. Och den tredje koefficienten, -4, blir en konstant, ett tal utan variabel, eftersom den ursprungliga variabeln var lika med x. Du kan skriva ett R bredvid 16, för detta är resten. Så här kommer det att se ut:
-2 0 8
1 0 -4 |16
X + 0X - 4 R 16
X - 4R16

12. Skriv ner det slutliga svaret. Detta är det nya polynomet, x - 4, plus resten, 16 som täljare och x + 2 som nämnare. Så här ser det ut: x - 4 +16/(x +2).
Tips
- För att kontrollera ditt svar, multiplicera kvoten med divisor och lägg till resten. Detta måste vara samma som det ursprungliga polynomet.
- (divisor)(kvot)+(resten)
- (X + 2)(X - 4) + 16
- Multiplicera med den yttre först, den inre sista metoden.
- (X - 4X + 2X - 8) + 16
- X + 2X - 4X - 8 + 16
- X + 2X - 4X + 8
"Dela polynom syntetiskt"
Оцените, пожалуйста статью