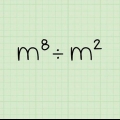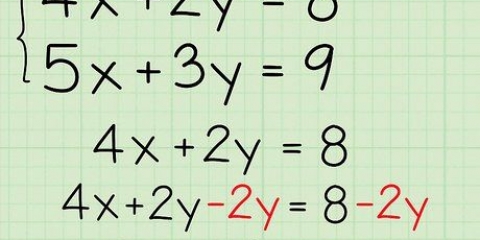Tio till tre styrka











Som visas här kan du fortsätta multiplicera basen med produkten av vart och ett av de första paren av siffror, tills du får det slutliga svaret. Fortsätt bara att multiplicera de två första siffrorna, multiplicera sedan detta svar med nästa tal i sekvensen. Detta gäller för vilken exponent som helst. När du är klar med exemplet får du  .
. 




Använd en sökmotor som Startpage, Duckduckgo eller Google för att hitta svaret. Du kan använda `^`-knappen på din dator, surfplatta eller smartphone för att skriva in uttrycket i sökrutan, så ser du omedelbart svaret och förslag på liknande uttryck att utforska (Duckduckgo visar till och med en komplett miniräknare ). 





Eftersom allt är samma tal, men multiplicerat, kan vi kombinera dessa: 




Eftersom baserna är desamma kan du bara lägga till dem: 




Som du kommer att se om ett ögonblick, vilket tal som helst som är en del av ett bråk, som t.ex  , skrivas om som
, skrivas om som  . Negativa exponenter bildar bråk.
. Negativa exponenter bildar bråk. 
 = 125
= 125 = 12
= 12 = -x^12
= -x^12 =
=  Kom ihåg att ett tal utan potens har exponenten 1
Kom ihåg att ett tal utan potens har exponenten 1 =
= 
 =
= 




![Lösa exponenter x^{{{frac{1}{3}}}}={sqrt[ {3}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/759eade6ce89e27b301ccdcd83d7e8858827b8e2)
 =
= ![Lösa exponenter ({sqrt[ {3}]{x}})^{5}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ea002d6365c3ba2d1d255162136605453a7135f)



Lösa exponenter
Exponenter används när ett tal multipliceras med sig själv. Istället för 



Steg
Metod 1 av 3: Lösa enkla exponenter

1. Lär dig rätt termer och ordförråd för exponentiella problem. Har du en exponent som  , sedan arbetar du med två enkla delar. Chassinumret här är en 2, eller bas. Detta nummer höjs till makten 3, även känd som exponent eller kraft. pratar vi om
, sedan arbetar du med två enkla delar. Chassinumret här är en 2, eller bas. Detta nummer höjs till makten 3, även känd som exponent eller kraft. pratar vi om  , då säger vi `två till tredje makten`, `två till tredje makten` eller `två höjningar till tredje makten`.`
, då säger vi `två till tredje makten`, `två till tredje makten` eller `två höjningar till tredje makten`.`
 , sedan arbetar du med två enkla delar. Chassinumret här är en 2, eller bas. Detta nummer höjs till makten 3, även känd som exponent eller kraft. pratar vi om
, sedan arbetar du med två enkla delar. Chassinumret här är en 2, eller bas. Detta nummer höjs till makten 3, även känd som exponent eller kraft. pratar vi om  , då säger vi `två till tredje makten`, `två till tredje makten` eller `två höjningar till tredje makten`.`
, då säger vi `två till tredje makten`, `två till tredje makten` eller `två höjningar till tredje makten`.` - Om ett tal höjs till andra potens, som t.ex
, då kan man också säga att numret är kvadratisk är ungefär fem i kvadrat.`
- Om ett tal höjs till tredje potens, som t.ex
, då kan man också säga att siffran a kubnummer är.
- Om ett tal utan exponent nämns, som till exempel 4, så står det i teorin i första potens och kan skrivas om som
.
- Om exponenten är lika med 0 och ett `tal (ej noll)` höjs till `nollpotens`, så är heltal 1, som
eller till och med något liknande
Mer om detta i avsnittet "Tips".

2. Multiplicera basen det antal gånger för sig självt som indikeras av exponenten. Om du ska lösa en potens för hand börjar du med att skriva om den som en multiplikation. Du multiplicerar basen antalet gånger med sig själv, vilket indikeras av exponenten. Så, har du  sedan multiplicerar du tre fyra gånger med sig själv
sedan multiplicerar du tre fyra gånger med sig själv  . Några fler exempel är:
. Några fler exempel är:
 sedan multiplicerar du tre fyra gånger med sig själv
sedan multiplicerar du tre fyra gånger med sig själv  . Några fler exempel är:
. Några fler exempel är:



3. Lös ett uttryck: Multiplicera de två första siffrorna tillsammans för att få produkten. Till exempel med  , börjar du med
, börjar du med  Det här verkar vara en tråkig uppgift, men gör det bara steg för steg. Börja multiplicera de två första fyrana. Ersätt sedan de två fyrorna med svaret som visas nedan:
Det här verkar vara en tråkig uppgift, men gör det bara steg för steg. Börja multiplicera de två första fyrana. Ersätt sedan de två fyrorna med svaret som visas nedan:
 , börjar du med
, börjar du med  Det här verkar vara en tråkig uppgift, men gör det bara steg för steg. Börja multiplicera de två första fyrana. Ersätt sedan de två fyrorna med svaret som visas nedan:
Det här verkar vara en tråkig uppgift, men gör det bara steg för steg. Börja multiplicera de två första fyrana. Ersätt sedan de två fyrorna med svaret som visas nedan:



4. Multiplicera svaret från det första paret (16) med nästa nummer. Fortsätt att multiplicera siffrorna för att "växa" din exponent. Om vi fortsätter med vårt exempel multiplicerar vi 16 med nästa 4 så att:






 .
.
5. Prova även följande exempel och kontrollera dina svar med en miniräknare.




6. Använd "exp", "X n  ` eller `^`-knappen på din miniräknare för exponenterna. Det är nästan omöjligt att hitta större exponenter, som t.ex
` eller `^`-knappen på din miniräknare för exponenterna. Det är nästan omöjligt att hitta större exponenter, som t.ex  för hand, men miniräknare kan hantera detta enkelt. Knappen för detta visas vanligtvis tillräckligt tydligt. Windows-kalkylatorn kan utökas till en vetenskaplig kalkylator genom att klicka på kalkylatorns "Visa"-flik och välja "Scientific". Om du vill ha tillbaka standardräknaren klickar du på "Visa" igen och väljer "Standard".
för hand, men miniräknare kan hantera detta enkelt. Knappen för detta visas vanligtvis tillräckligt tydligt. Windows-kalkylatorn kan utökas till en vetenskaplig kalkylator genom att klicka på kalkylatorns "Visa"-flik och välja "Scientific". Om du vill ha tillbaka standardräknaren klickar du på "Visa" igen och väljer "Standard".
 ` eller `^`-knappen på din miniräknare för exponenterna. Det är nästan omöjligt att hitta större exponenter, som t.ex
` eller `^`-knappen på din miniräknare för exponenterna. Det är nästan omöjligt att hitta större exponenter, som t.ex  för hand, men miniräknare kan hantera detta enkelt. Knappen för detta visas vanligtvis tillräckligt tydligt. Windows-kalkylatorn kan utökas till en vetenskaplig kalkylator genom att klicka på kalkylatorns "Visa"-flik och välja "Scientific". Om du vill ha tillbaka standardräknaren klickar du på "Visa" igen och väljer "Standard".
för hand, men miniräknare kan hantera detta enkelt. Knappen för detta visas vanligtvis tillräckligt tydligt. Windows-kalkylatorn kan utökas till en vetenskaplig kalkylator genom att klicka på kalkylatorns "Visa"-flik och välja "Scientific". Om du vill ha tillbaka standardräknaren klickar du på "Visa" igen och väljer "Standard".Metod 2 av 3: Addera, subtrahera och multiplicera exponenter

1. Du kan bara addera eller subtrahera potenstal från varandra om de har samma bas och samma exponent. Om du har att göra med identiska baser och exponenter, som t.ex  , då kan du förenkla additionen av termerna till en multiplikation. Glöm inte att
, då kan du förenkla additionen av termerna till en multiplikation. Glöm inte att  kan betraktas som
kan betraktas som  , så att
, så att  genom att lägga till, där "1 av det + 1 av det = 2 av det", vad "det" än kan vara. Lägg bara ihop antalet liknande termer (de med identisk bas och exponent) och multiplicera summan med det exponentiella uttrycket. Du kan då
genom att lägga till, där "1 av det + 1 av det = 2 av det", vad "det" än kan vara. Lägg bara ihop antalet liknande termer (de med identisk bas och exponent) och multiplicera summan med det exponentiella uttrycket. Du kan då  lösa och multiplicera det svaret med två. Kom ihåg att detta är möjligt eftersom en multiplikation inte är något annat än att skriva om en addition, eftersom
lösa och multiplicera det svaret med två. Kom ihåg att detta är möjligt eftersom en multiplikation inte är något annat än att skriva om en addition, eftersom  . Här är några exempel:
. Här är några exempel:
 , då kan du förenkla additionen av termerna till en multiplikation. Glöm inte att
, då kan du förenkla additionen av termerna till en multiplikation. Glöm inte att  kan betraktas som
kan betraktas som  , så att
, så att  genom att lägga till, där "1 av det + 1 av det = 2 av det", vad "det" än kan vara. Lägg bara ihop antalet liknande termer (de med identisk bas och exponent) och multiplicera summan med det exponentiella uttrycket. Du kan då
genom att lägga till, där "1 av det + 1 av det = 2 av det", vad "det" än kan vara. Lägg bara ihop antalet liknande termer (de med identisk bas och exponent) och multiplicera summan med det exponentiella uttrycket. Du kan då  lösa och multiplicera det svaret med två. Kom ihåg att detta är möjligt eftersom en multiplikation inte är något annat än att skriva om en addition, eftersom
lösa och multiplicera det svaret med två. Kom ihåg att detta är möjligt eftersom en multiplikation inte är något annat än att skriva om en addition, eftersom  . Här är några exempel:
. Här är några exempel: 
2. Multiplicera tal med samma bas genom att addera exponenterna. Om du har två exponenter med samma bas, som t.ex  , sedan behöver du bara lägga till de två exponenterna med samma bas. Så,
, sedan behöver du bara lägga till de två exponenterna med samma bas. Så, . Om du tycker att detta är lite konstigt, dela upp det i mindre delar för att förstå hur systemet fungerar:
. Om du tycker att detta är lite konstigt, dela upp det i mindre delar för att förstå hur systemet fungerar:
 , sedan behöver du bara lägga till de två exponenterna med samma bas. Så,
, sedan behöver du bara lägga till de två exponenterna med samma bas. Så, . Om du tycker att detta är lite konstigt, dela upp det i mindre delar för att förstå hur systemet fungerar:
. Om du tycker att detta är lite konstigt, dela upp det i mindre delar för att förstå hur systemet fungerar:






3. Multiplicera ett exponentiellt tal upphöjt till en annan potens, t.ex ( X 2 ) 5  . Om du höjer ett tal till en viss potens, och hela höjs till en viss potens, multiplicera bara de två exponenterna. Så,
. Om du höjer ett tal till en viss potens, och hela höjs till en viss potens, multiplicera bara de två exponenterna. Så,  . Om du blir förvirrad, tänk igen vad dessa symboler egentligen betyder.
. Om du blir förvirrad, tänk igen vad dessa symboler egentligen betyder.  menar bara dig
menar bara dig  Multiplicerar 5 gånger av sig själv, så:
Multiplicerar 5 gånger av sig själv, så:
 . Om du höjer ett tal till en viss potens, och hela höjs till en viss potens, multiplicera bara de två exponenterna. Så,
. Om du höjer ett tal till en viss potens, och hela höjs till en viss potens, multiplicera bara de två exponenterna. Så,  . Om du blir förvirrad, tänk igen vad dessa symboler egentligen betyder.
. Om du blir förvirrad, tänk igen vad dessa symboler egentligen betyder.  menar bara dig
menar bara dig  Multiplicerar 5 gånger av sig själv, så:
Multiplicerar 5 gånger av sig själv, så:



4. Tänk på negativa exponenter som bråk, eller den reciproka av talet. Vet inte vad en ömsesidighet är, inga problem. Om du har att göra med en negativ exponent, som t.ex  , gör sedan exponenten positiv och placera denna som nämnaren under ett, vilket resulterar i
, gör sedan exponenten positiv och placera denna som nämnaren under ett, vilket resulterar i  . Här är några ytterligare exempel:
. Här är några ytterligare exempel:
 , gör sedan exponenten positiv och placera denna som nämnaren under ett, vilket resulterar i
, gör sedan exponenten positiv och placera denna som nämnaren under ett, vilket resulterar i  . Här är några ytterligare exempel:
. Här är några ytterligare exempel:


5. Dela två tal med samma bas genom att subtrahera exponenterna. Division är motsatsen till multiplikation, och även om de inte löses exakt som motsatser, är de här. Om du har att göra med ekvationen  , subtrahera bara den översta exponenten från den nedre och lämna basen som den är. Så,
, subtrahera bara den översta exponenten från den nedre och lämna basen som den är. Så,  , eller 16.
, eller 16.
 , subtrahera bara den översta exponenten från den nedre och lämna basen som den är. Så,
, subtrahera bara den översta exponenten från den nedre och lämna basen som den är. Så,  , eller 16.
, eller 16. , skrivas om som
, skrivas om som  . Negativa exponenter bildar bråk.
. Negativa exponenter bildar bråk.
6. Prova några övningar för att vänja dig vid att arbeta med potenstal. Följande övningar tränar allt som har behandlats hittills. För svaret, välj bara raden som innehåller problemet.
 = 125
= 125 = 12
= 12 = -x^12
= -x^12 =
=  Kom ihåg att ett tal utan potens har exponenten 1
Kom ihåg att ett tal utan potens har exponenten 1 =
= 
 =
= 
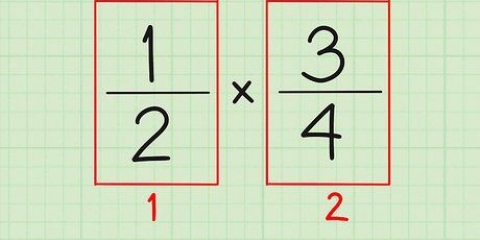
Metod 3 av 3: Lösa bråk som potenstal

1. Behandla bråk i form av potenstal, som t.ex X 1 2  som en kvadratrot.
som en kvadratrot.  är faktiskt exakt samma som
är faktiskt exakt samma som  . Detta är sant oavsett bråkets nämnare, så
. Detta är sant oavsett bråkets nämnare, så  blir kvadratiska roten av x, även skrivet som
blir kvadratiska roten av x, även skrivet som ![Lösa exponenter {sqrt[ {4}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6193130540098748b8aecf0b95bf490c2ae3d867) .
.
 som en kvadratrot.
som en kvadratrot.  är faktiskt exakt samma som
är faktiskt exakt samma som  . Detta är sant oavsett bråkets nämnare, så
. Detta är sant oavsett bråkets nämnare, så  blir kvadratiska roten av x, även skrivet som
blir kvadratiska roten av x, även skrivet som ![Lösa exponenter {sqrt[ {4}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6193130540098748b8aecf0b95bf490c2ae3d867) .
. - Rötter är motsatsen till exponenter. Till exempel om du tar svaret på
till fjärde makten, då kommer du tillbaka till
, och så kan
också skrivas som
. Ett annat exempel är
och då
och sålunda
.

2. Gör täljaren till en normalexponent för en blandad bråkdel. kan se omöjligt ut, men är lätt om du kommer ihåg hur exponenter multipliceras. Gör basen till en kvadratrot, som en normal bråkdel, och höj det hela till styrkan överst i bråket. Om du har svårt att komma ihåg detta, gå igenom teorin igen. I slutändan gäller det
kan se omöjligt ut, men är lätt om du kommer ihåg hur exponenter multipliceras. Gör basen till en kvadratrot, som en normal bråkdel, och höj det hela till styrkan överst i bråket. Om du har svårt att komma ihåg detta, gå igenom teorin igen. I slutändan gäller det  bara lika
bara lika  Till exempel:
Till exempel:
 kan se omöjligt ut, men är lätt om du kommer ihåg hur exponenter multipliceras. Gör basen till en kvadratrot, som en normal bråkdel, och höj det hela till styrkan överst i bråket. Om du har svårt att komma ihåg detta, gå igenom teorin igen. I slutändan gäller det
kan se omöjligt ut, men är lätt om du kommer ihåg hur exponenter multipliceras. Gör basen till en kvadratrot, som en normal bråkdel, och höj det hela till styrkan överst i bråket. Om du har svårt att komma ihåg detta, gå igenom teorin igen. I slutändan gäller det  bara lika
bara lika  Till exempel:
Till exempel:

![Lösa exponenter x^{{{frac{1}{3}}}}={sqrt[ {3}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/759eade6ce89e27b301ccdcd83d7e8858827b8e2)
 =
= ![Lösa exponenter ({sqrt[ {3}]{x}})^{5}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ea002d6365c3ba2d1d255162136605453a7135f)

3. Du kan addera, subtrahera och multiplicera bråk i form av potenstal – precis som du brukar. Det är mycket lättare att lägga till eller subtrahera exponenterna innan man löser eller omvandlar dem till kvadratrötter. Om basen är densamma och exponenten är densamma, kan du bara addera och subtrahera dem. Om bara basen är densamma kan du multiplicera och dividera exponenterna som vanligt, så länge du tar hänsyn till hur man adderar och subtraherar bråk. Till exempel:


Tips
- De flesta miniräknare har en knapp för exponenter - att trycka på efter att ha angett basen - för att lösa problem med potenstal.Vanligtvis ser detta ut som en ^ eller x^y.
- "Förenkla" betyder i matematik gör de redigeringar som behövs för att få den enklaste formen av uttrycken i fråga.
- 1 är identitetselementet för exponenter. Det betyder att varje reellt tal som höjs till 1 potens (till första potens) är själva talet, till exempel:
Dessutom är 1 identitetselementet för multiplikation (1 som multiplikator, t.ex
), och från division (1 som utdelning, som t.ex
.
- Basen noll till noll (0) är odefinierad (engelska: dne, existerar inte). Datorer eller miniräknare kommer då att returnera ett "fel". Kom ihåg att alla tal som inte är noll höjt till 0-potensen alltid är lika med 1,
- Till exempel är högre matematik för imaginära tal,
, varigenom
; e är en irrationell, kontinuerlig konstant lika med 2,71828..., och a är en godtycklig konstant. Beviset finns i de flesta högre matematikböcker.
Varningar
- En exponentiell ökning gör att produkten stiger snabbare och snabbare, så att svaret kan visas fel, när det är korrekt. (Kontrollera detta genom att till exempel rita en exponentialfunktion.: 2, om x har ett intervall med olika värden).
"Lösa exponenter"
Оцените, пожалуйста статью