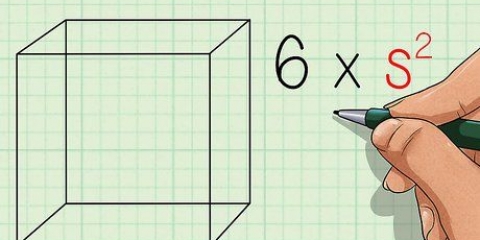
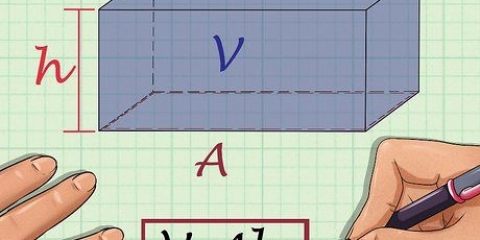
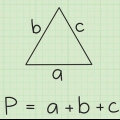Hur man beräknar omkretsen av en polygon

Steg

En polygon är vilken tvådimensionell form som helst som har raka linjer. Det finns både vanliga polygoner (de med lika sidor) och oregelbundna polygoner (de med olika sidolängder). Metoderna för att hitta omkretsen av regelbundna och oregelbundna polygoner är lite olika, men båda är lätta när du väl vet vad du ska göra. Du kan också hitta dess omkrets på ett koordinatnät. Om du försöker hitta omkretsen av en vanlig polygon, använd formeln: omkrets = antal sidor x längden på varje sida.

Steg

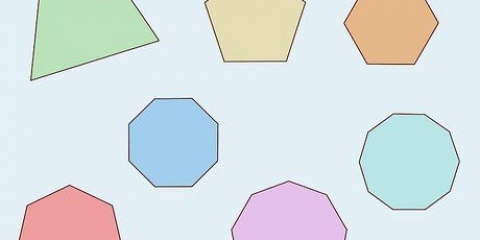
Metod 1 av 3: Hitta omkretsen av en vanlig polygon

1. Kontrollera om alla sidor av polygonen är lika långa. Reguljära polygoner är polygoner med lika sidor. Om sidorna av polygonen du tittar på inte alla är lika långa, måste du hitta omkretsen med den oregelbundna polygonmetoden. Om sidorna är lika långa har du att göra med en vanlig polygon.

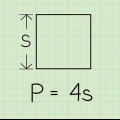
Dricks: Om vissa sidor inte är märkta, titta på resten av polygonen för att bestämma längderna. Till exempel, om du har en kvadrat där bara en sida har en given längd, så vet du att de andra sidorna har samma längd, eftersom rutor har lika sidor.

Bild med titeln Hitta omkretsen av en polygon Steg 2

2. Skriv ner längden på en sida av polygonen. Det spelar ingen roll vilken sida du väljer, eftersom alla sidlängder är lika. Se bara till att du bara skriver ner längden på en av sidorna.

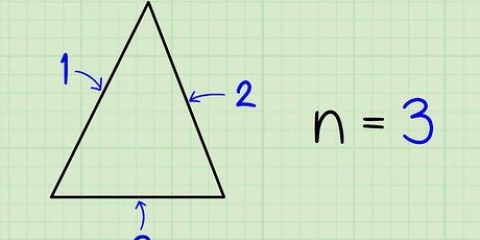
Anta till exempel att du har att göra med en kvadrat med en sidolängd på sex, skulle du skriva "6".

Bild med titeln Hitta omkretsen av en polygon Steg 3

3. Skriv ner det totala antalet sidor som polygonen har. Oroa dig inte för längden på sidorna vid denna tidpunkt. Räkna bara hur många sidor polygonen har och skriv ner det.

För en kvadrat skriver du `4` eftersom en kvadrat har fyra sidor.

Bild med titeln Hitta omkretsen av en polygon Steg 4

4. Multiplicera längden på sidan med antalet sidor för att få omkretsen. Formeln för att hitta omkretsen av en vanlig polygon är helt enkelt antalet sidor gånger längden på vilken sida som helst. Om du multiplicerade dessa två siffror tillsammans har du hittat polygonens omkrets!

I exemplet med kvadraten vet du att kvadraten har en sidolängd på sex och totalt fyra sidor. Därför kan du bara beräkna kvadratens omkrets med 6 x 4 = 24.

Eller anta att du har att göra med en triangel med en sidolängd på tre. Eftersom en triangel har tre sidor, skulle du göra 3 (antalet sidor) x 3 (sidans längd) = 9. Så omkretsen av triangeln är 9.

Metod 2 av 3: Beräkna omkretsen av en oregelbunden polygon

Bild med titeln Hitta omkretsen av en polygon Steg 5

1. Bestäm från längden på polygonen om den är oregelbunden. En oregelbunden polygon är en polygon utan lika sidor. Om polygonens sidor alla är lika långa betyder det att polygonen är regelbunden, inte oregelbunden.

Visste du? Du kan använda samma metod för att hitta omkretsen av en oregelbunden polygon för att hitta omkretsen av en vanlig polygon, men inte tvärtom.

Bild med titeln Hitta omkretsen av en polygon Steg 6

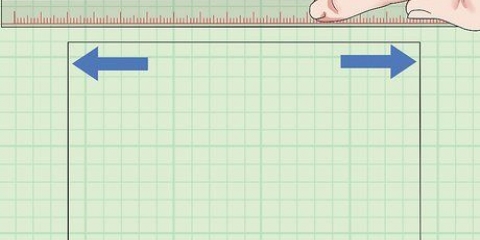
2. Skriv ner längden på varje sida av polygonen. Eftersom inte alla sidor av en oregelbunden polygon är lika, måste du skriva ner varje enskild sida. Även om vissa sidor är lika, måste du fortfarande skriva ner varje längd separat.

Till exempel, om du har en rektangel med två sidor längd 4 och två sidor längd 3, kan du skriva: `4, 4, 3, 3`.

Om du arbetar med en oregelbunden polygon med en sida på 2, en sida på 3 och en sida på 4 enheter lång, kan du skriva: `2, 3, 4`.

Bild med titeln Hitta omkretsen av en polygon Steg 7

3. Lägg ihop alla längderna för att hitta omkretsen. För att hitta omkretsen av en oregelbunden polygon behöver du bara hitta summan av alla sidor. Lägg bara ihop längden på varje sida du skrev ner för att hitta polygonens omkrets!

Till exempel, om sidolängderna för polygonen var 4, 4, 3 och 3, är summan lika med 14. Därför är 14 polygonens omkrets.

Metod 3 av 3: Bestämning av omkretsen med hjälp av givna koordinater

Bild med titeln Hitta omkretsen av en polygon Steg 8

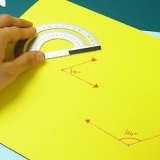
1. Rita ett koordinatsystem med en x- och y-axel. Ett koordinatsystem är en graf med en x- och y-axel på vilken du kan ange koordinater. För att rita ett koordinatsystem, ta ett ark diagrampapper eller rita dina egna rutnätslinjer på ett tomt papper med hjälp av en linjal. Dra sedan en horisontell linje genom mitten för x-axeln och en vertikal linje genom mitten för y-axeln. Numrera slutligen punkterna på varje axel, börja med `0` där x-axeln och y-axeln skär varandra.

När du numrerar koordinatsystemet kommer siffrorna ovanför och till höger om 0:an att vara positiva, medan talen under och till vänster om 0:an är negativa.

Bild med titeln Hitta omkretsen av en polygon Steg 9

2. Ange de givna koordinaterna på grafen. Du borde ha fått koordinater för varje hörn av polygonen vars omkrets du försöker hitta. Varje koordinat ska se ut som `(1,2)`. Använd siffrorna du markerat på koordinatsystemet för att ange var och en av koordinaterna. När du är klar, koppla ihop dessa punkter med raka linjer för att se formen på polygonen du arbetar med.

Dricks: När du anger koordinaterna, kom ihåg att den första siffran representerar x-axeln och den andra siffran representerar y-axeln. Om du till exempel säger (2.4) går du till 2 på x-axeln och därifrån till 4 upp på y-axeln och markerar den punkten i rutnätet.

Bild med titeln Hitta omkretsen av en polygon Steg 10

3. Hitta vertikala och horisontella längder av sidor genom att räkna enheterna. Du måste veta längden på varje sida av polygonen för att bestämma dess omkrets. För vertikala eller horisontella sidor, räkna bara hur många enheter det finns mellan prickarna i varje ände. Skriv sedan numret bredvid den sidan så att du kan hänvisa till det senare.

Till exempel, om du försöker hitta längden på en horisontell sida, börja i ena änden och räkna antalet rutor mellan den punkten och den andra änden. Om du räknar sex, skulle det betyda att längden på den sidan är 6 enheter.

Bild med titeln Hitta omkretsen av en polygon Steg 11

4.Använd avståndsformeln för att hitta längden på diagonala sidor. Tyvärr kan du inte räkna enheterna på ett rutnät för att hitta längden på de diagonala sidorna som du kan med vertikala eller horisontella sidor (eftersom du har att göra med heltal). Du kan använda distansformeln istället:

d = \sqrt{(X} 2 - X_{1})^{2} + (y_{2} - y_{1})^{2}

$d={sqrt{(x_{{2}}-x_{{1}})^{{2}}+(y_{{2}}-y_{{1}})^{{2}}} }$ . Ange bara värdena för x- och y-koordinaterna för de två punkterna i ändarna av sidan du försöker hitta och lös formeln för att hitta längden.

Om du till exempel försöker hitta avståndet (längden) mellan två punkter med koordinater (4.7) och (1.3), använder du dessa koordinater i formeln och får:

d = \sqrt{(4} 2 - 1_{1})^{2} + (7_{2} - 3_{1})^{2}

${displaystyle d={sqrt {(4_{2}-1_{1})^{2}+(7_{2}-3_{1})^{2}}}}$

Sedan kan du förenkla ekvationen och få:

d = \sqrt{25}

$d={sqrt{25}}$ .

Till slut släppte du taget

d = \sqrt{25}

$d={sqrt{25}}$ på och du får 5 som svar. Så längden på sidan är 5.

Bild med titeln Hitta omkretsen av en polygon Steg 12

5. Lägg ihop längden på varje sida för att hitta polygonens omkrets. Omkretsen av en polygon är lika med summan av alla sidolängder. När du har bestämt alla dessa längder med hjälp av koordinaterna du har fått, är allt du behöver göra att lägga ihop dem och du är klar!

Om du till exempel har ritat ut koordinaterna för en triangel och du finner att sidlängderna är 3, 2 och 5, adderar du dessa siffror för att få 10. Så omkretsen av triangeln är 10.