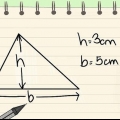
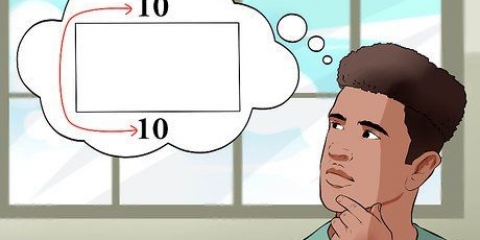
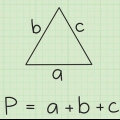Vilken sida av triangeln som helst kan vara basen, oavsett hur triangeln är ritad. För att föreställa dig detta, rotera triangeln i ditt sinne tills den alltför välbekanta sidan har blivit botten. Till exempel, om du vet att arean av en triangel är 20, och en av dess sidor är 4, då: A = 20 och b = 4. 
I exemplet: 20 = 1/2(4)h 20 = 2 timmar 10 = h 

Så i exemplet:c = 8 och a = 4. 
4 + b = 8 16 + b = 64 b = 48 
b = Sqrt (48) = 6,93
Beräkna höjden på en triangel
För att beräkna arean av en triangel behöver du dess höjd. Om denna information inte ges kan du enkelt beräkna den utifrån vad du vet! Den här artikeln kommer att lära dig två olika sätt att hitta höjden på en triangel, beroende på vilken information du har fått.
Steg
Metod 1 av 2: Bestämma höjden när arean och basen är kända

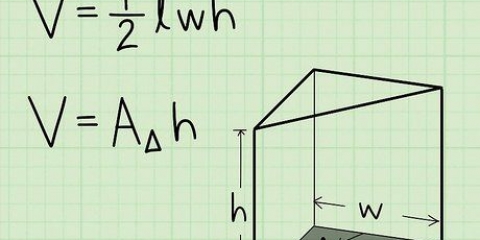
1. Formeln för arean av en triangel. Detta ärA=1/2bh.
- a = Triangelns area
- b = Längden på triangelns bas
- h = Höjd på triangelns bas

2. Titta på triangeln och bestäm vilka variabler som är kända. I det här fallet känner du redan till området, så a är lika med det värdet.Du bör också känna till värdet av en av sidorna; ange det värdet "`b`".Om du inte känner till båda värdena eller ett av dem behöver du en annan metod.

3. Använd dina värden i ekvationenA=1/2bh och beräkna. Multiplicera först basen (b) med 1/2, dividera sedan arean (A) med produkten.Det resulterande värdet är höjden på din triangel!
Metod 2 av 2: Hitta höjden på en liksidig triangel

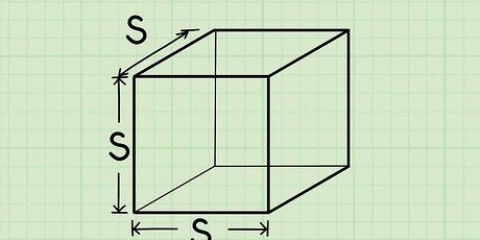
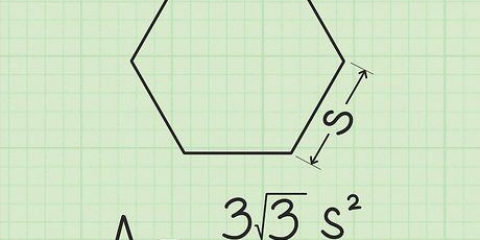
1. Egenskaperna för en liksidig triangel. En liksidig triangel har tre lika sidor och tre lika vinklar på 60 grader vardera. Om du delar en liksidig triangel på mitten kommer du att få två kongruenta rätvinkliga trianglar.
- I det här exemplet kommer vi att använda en liksidig triangel med sidor som har en längd på 8.
2. Pythagoras sats. Pythagoras sats säger att för en rätvinklig triangel med längdsidor a och b, och en hypotenusa av längd c: a + b = c.Vi kan använda denna sats för att hitta höjden på vår liksidiga triangel!

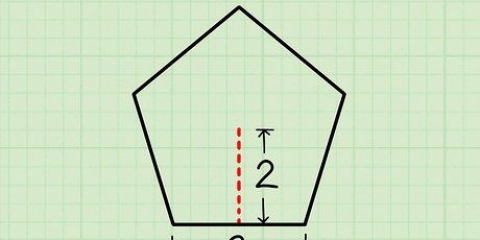
3. Dela den liksidiga triangeln på mitten och tilldela värden till variablernaa, b ochc.Sida a är lika med halva längden av en sida och sida b är höjden på triangeln vi vill lösa.

4. Fyll i värdena i Pythagoras sats och lös b. Beräkna först kvadraten på c och a genom att multiplicera den med sig själv. Subtrahera sedan a från c.

5. Hitta kvadratroten ur b för att hitta höjden på triangeln! Använd kvadratroten på din kalkylator för att hitta Sqrt(. Svaret är höjden på din liksidiga triangel!
"Beräkna höjden på en triangel"
Оцените, пожалуйста статью