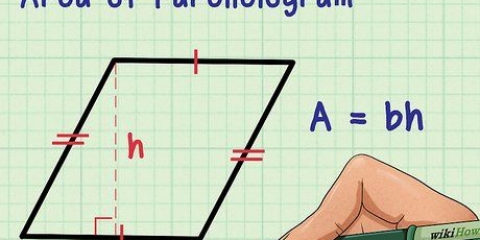Formeln för att beräkna längden på apotem är som följer: längden på sidan (s) dividerat med 2 gånger tangenten (tan) på 180 grader, dividerat med antalet sidor (n). 

Omkretsen är 6 x 10 (n X s) är lika med 60 (så sid = 60). Apotem beräknas genom att koppla in 6 och 10 för n och s av formeln. Resultatet av 2tan(180/6) är 1,1547, och sedan dividerar vi 10 med 1,1547 - vilket är lika med 8,66. Polygonens area är a = a X sid / 2 eller 8,66 multiplicerat med 60 delat med 2. Lösningen är ett område på 259,8. Observera att det inte finns några parenteser i "yta"-ekvation, så 8,66 dividerat med 2 multiplicerat med 60 ger samma resultat, precis som 60 dividerat med 2 multiplicerat med 8,66. 


Hitta området för vanliga polygoner
En vanlig polygon är en tvådimensionell konvex figur med kongruenta sidor och lika vinklar. För många polygoner, som t.ex fyrhörningar eller trianglar Det finns enkla formler för att hitta deras område, men om du har att göra med en polygon är det förmodligen bäst att välja en formel som använder apotem och formens omkrets. Med lite ansträngning kan du hitta arean av vanliga polygoner på bara några minuter.
Steg
Del 1 av 2: Beräkna omkretsen

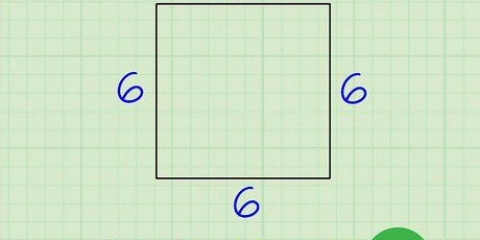
1. Beräkna omkretsen. Omkretsen är den kombinerade längden av omkretsen av en tvådimensionell figur. För en vanlig polygon kan detta beräknas genom att multiplicera längden på en sida med antalet sidor (n) av figuren.

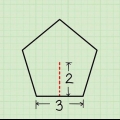
2. Bestäm apotem. Apotemet för en vanlig polygon är det kortaste avståndet från dess centrum till vardera sidan, vilket skapar en rät vinkel. Detta är lite svårare att avgöra än omkretsen.

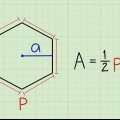
3. Lär dig rätt formel. Arean av en vanlig polygon ges av formeln:Area = (a X sid)/2,varigenom a är längden på apotem, och sid polygonens omkrets.

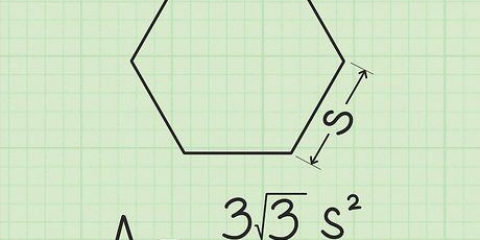
4. Ange värdena föra och sid i formeln för att beräkna omkretsen. Som ett exempel, låt oss ta en hexagon (6 sidor) med längden 10 för varje sida (s).
Del 2 av 2: Att förstå begreppen på ett annat sätt

1. En vanlig polygon kan betraktas som en samling trianglar. Varje sida representerar basen av en triangel, och det finns lika många trianglar i polygonen som det finns sidor. Var och en av trianglarna är lika i bas, höjd och area.

2. Använd formeln för arean av en triangel. Arean av en triangel är 1/2 av dess bas (som är lika med en sida av en polygon), multiplicerad med dess höjd (vilket är samma som apotem för en vanlig polygon).

3. Lägg märke till likheterna. Återigen är formeln för en vanlig polygon 1/2 gånger apotem multiplicerad med omkretsen. Omkretsen är längden på en sida multiplicerad med antalet sidor (n); vid en vanlig polygon representerar n även antalet trianglar som utgör figuren. Så formeln är inget annat än arean av en triangel multiplicerat med antalet trianglar i polygonen.
Tips
- Se wikiHow för mer information om att arbeta med kvadratrötter och kubrötter.
- Om ritningen av din oktagon (eller vilken form som helst för den delen) är uppdelad i trianglar och arean av en triangel är märkt, behöver du inte apotemet längre. Ta bara arean av den ena triangeln och multiplicera den med antalet sidor i den ursprungliga polygonen.
"Hitta området för vanliga polygoner"
Оцените, пожалуйста статью