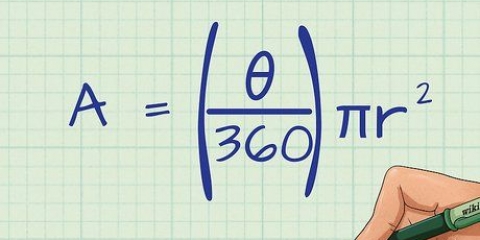Se apotem som "x√3"-sidan av en 30-60-90 triangel. Du kan se det så här eftersom hexagonen består av sex liksidiga trianglar. Apotemet skär en av dessa trianglar på mitten och skapar en triangel med vinklar på 30, 60 och 90 grader. Du vet att sidan mitt emot 60 graders vinkeln har längden x√3, sidan mitt emot 30 graders vinkeln har längden x, och sidan mitt emot 90 graders vinkeln har längden 2x. Om 10√3 står för "x√3," då vet du att x = 10. Du vet att x är halva längden av triangelns botten. Dubbla detta för att bestämma full längd. Så botten av triangeln är 20. Det finns sex av dessa sidor i hexagonen, så för att hitta hexagonens omkrets multiplicerar vi 20 med 6 = 120. 
Area = 1/2 x 120 x 10√3 Area = 60 x 10√3 Area = 600√3 


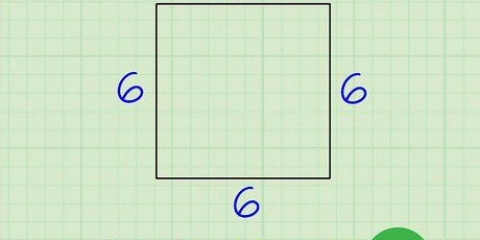
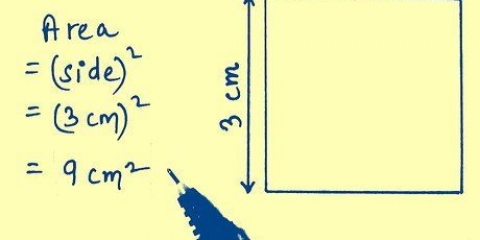
Om du har en kvadrat med sidor av längden 6, är arean 6 x 6 = 36. 
Om basen av en rektangel är 4 och höjden är 3, så är arean 4 x 3 = 12. 
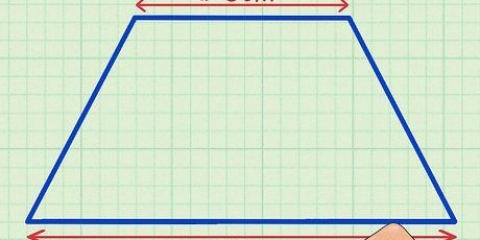
Anta att du har en trapets vars baser har längderna 6 och 8 och vars höjd är 10. Då är arean [(6 + 8) x 10]/2, vilket kan förenklas till (14 x 10)/2 eller 140/2, vilket är en area på 70. 





Beräkna arean av en polygon
Att beräkna arean av en polygon kan vara väldigt enkelt när det kommer till en vanlig triangel. Men det blir mycket svårare när det kommer till en oregelbunden form med elva sidor. Om du vill veta hur man beräknar arean av olika polygoner, följ dessa steg.
Steg
Del 1 av 3: Beräkna arean av polygoner med hjälp av apotem

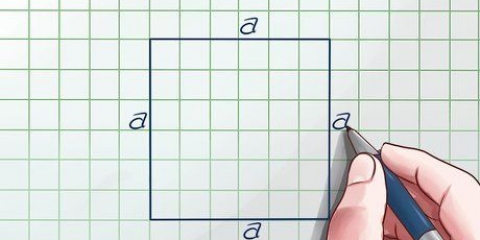
1. Skriv formeln för att hitta arean av en vanlig polygon. För att hitta arean av en vanlig polygon behöver du bara följa formeln: area = 1/2 x omkrets x apotem. Det betyder följande:
- Omkrets = summan av längderna på alla sidor
- Apotem = segmentet och även avståndet från mitten av polygonen till mitten av en sida

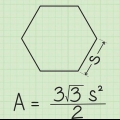
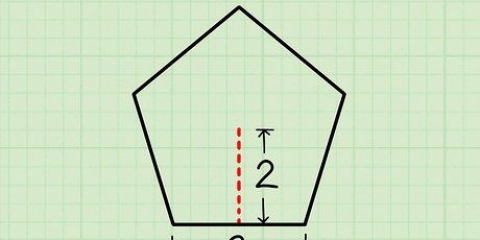
2. Bestäm apotem för polygonen. Om du använder apotemmetoden kommer apotem alltid att vara given. Anta att du arbetar med en hexagon vars apotem har en längd på 10√3.

3. Bestäm polygonens omkrets. Om omkretsen är given är du nästan klar. Men förmodligen är bara apotem given. Om du vet att det är en vanlig polygon kan du använda apotem för att bestämma dess omkrets. Det är så du gör det:

4. Nu kan vi sätta apotem och omkrets i formeln. Ännu en gång: area = 1/2 x omkrets x apotem, omkretsen är 120 och apotem är 10√3. Då ser formeln ut så här:

5. Förenkla ditt svar. Du kanske borde skriva resultatet med decimaler istället för en radikal. Använd din kalkylator för att hitta den ungefärliga kvadratroten ur tre och multiplicera det med 600. √3 x 600 = 1,039.2. Det är resultatet i decimaler.
Del 2 av 3: Hitta arean av en vanlig polygon med hjälp av andra formler

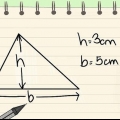
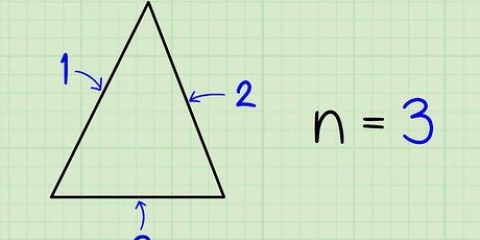
1. Beräkna arean av en jämn triangel. Om du vill hitta arean av en vanlig triangel kan du använda denna formel: area = 1/2 x bas x höjd.
- Om du har en triangel med basen 10 och höjden 8, då är arean 1/2 x 8 x 10 = 40.

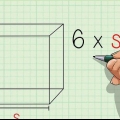
2. Beräkna arean av en kvadrat. För att hitta arean av en kvadrat behöver du bara multiplicera en av dess sidor med sig själv, eftersom basen och höjden är lika för en kvadrat.

3. Beräkna arean av en rektangel. För att hitta arean av en rektangel behöver du bara multiplicera dess bas med dess höjd.

4.Beräkna arean av en trapets. För att hitta arean av en trapets kan du använda följande formel: area = [(bas 1 + bas 2) x höjd]/2.
Del 3 av 3: Hitta arean för en oregelbunden polygon

1. Använd nodernas koordinater för att beräkna arean. Om du känner till koordinaterna kan du beräkna arean av en oregelbunden polygon.

2. Skapa en sekvens. Lista x- och y-koordinaterna för varje vertex i polygonen, moturs. Upprepa koordinaterna för den första punkten längst ner i listan.

3. Multiplicera x-koordinaten för varje vertex med y-koordinaten för nästa vertex. Lägg ihop resultaten. Summan av dessa produkter är 82.

4. Multiplicera y-koordinaten för varje vertex med x-koordinaten för nästa vertex. Lägg ihop resultaten. Summan av dessa produkter är -38.

5. Subtrahera summan av produkterna beräknade i steg 4 från summan av produkterna beräknade i steg 3. (82) - (-38) = 120.

6. Dividera detta resultat med 2 för att hitta arean av polygonen. Area = 120/2 = 60.
Tips
- Om du listar punkterna medurs istället för moturs får du också arean, men negativ. Du kan till exempel använda detta som ett verktyg för att bestämma den cykliska sekvensen av en uppsättning punkter som bildar en polygon.
- Denna formel beräknar area med orientering. Om du använder den på en form där två av linjerna skär varandra som i en 8:a, får du motursområdet minus medursområdet.
"Beräkna arean av en polygon"
Оцените, пожалуйста статью