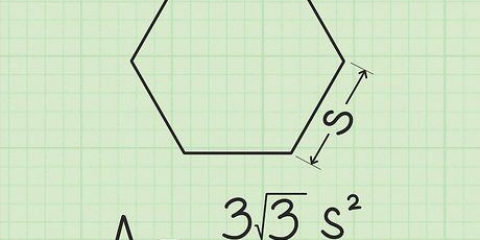
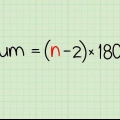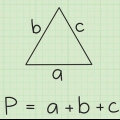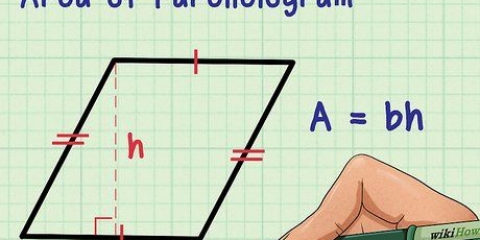Vinklarna i en triangel (en 3-sidig polygon) är totalt 180 grader. Vinklarna i en fyrhörning (en 4-sidig polygon) är totalt 360 grader. Vinklarna i en femhörning (en 5-sidig polygon) är totalt 540 grader. Vinklarna i en hexagon (en 6-sidig polygon) är totalt 720 grader. Vinklarna i en oktagon (en 8-sidig polygon) är totalt 1080 grader. 
Om polygonen är en vanlig polygon, dividera bara summan av alla vinklar med antalet vinklar. Således är vilken vinkel som helst i en liksidig triangel 180/3=60 grader, och vilken vinkel som helst i en kvadrat är 360/4=90 grader. (Även om en rektangel per definition inte är en vanlig polygon, är alla vinklar också räta vinklar och därför 90 grader). Om en polygon inte är en vanlig polygon måste du veta storleken på de andra vinklarna för att beräkna storleken på den okända vinkeln. gå till nästa steg. 
Om två av vinklarna i en triangel är 60 och 80 grader, addera dessa vinklar (60 + 80=140). Subtrahera sedan denna summa från summan av vinklarna i en triangel, 180 grader: 180-140=40 grader. (En sådan triangel, där alla vinklar är olika, kallas en skalentriangel). Du kan skriva ut metoden ovan som en formel: a=180 – (b + c), varvid a är vinkeln du vill bestämma, och b och c de vinklar som är kända. För polygoner med fler än 3 sidor, ersätt "180" med summan av vinklarna som är specifika för den polygonen och lägg till en annan term för varje ytterligare känd vinkel. För vissa polygoner är en "snabbare lösning" möjlig för att bestämma den okända vinkeln. En likbent triangel är en triangel med två lika långa sidor och två lika stora vinklar. Ett parallellogram är en fyrhörning med motsatta sidor av lika långa och diagonalt motsatta vinklar av samma storlek. 

Om du vet längden på den motsatta sidan (i förhållande till vinkeln) och längden på hypotenusan (sidan mitt emot den räta vinkeln), använd sinusfunktionen (längden på den motsatta sidan dividerat med hypotenusans längd). silke). Om du vet längden på den intilliggande rektangulära sidan och längden på hypotenusan kan du använda cosinusfunktionen (längden på den intilliggande sidan dividerad med hypotenusans längd). Om du känner till längden på de motsatta sidorna och intilliggande sidor kan du använda tangentfunktionen (längden på den motsatta sidan dividerad med längden på den intilliggande sidan). 
Att dividera det motsatta värdet 5 med hypotenusan (hypotenusan) 10 ger bråkdelen 5 / 10=0,5. 
Dagarna före räknare bör du konsultera en tryckt värdetabell för sinus, cosinus och tangens för vinklar från 0 till 90 grader. Följ sinuskolumnen tills du hittar värdet `0,5` och hitta sedan vinkeln som motsvarar det sinusvärdet. Om du har en miniräknare med trigonometriska funktioner kan du ange sinus som värdet (om du inte redan har använt räknaren för att dividera motsatsen med hypotenusan för att hitta detta värde) och sedan trycka på lämplig tangent eller tangenter. Beroende på räknarens märke, tryck på en enstaka tangent märkt `sin` eller en tangent märkt `Inv`, `2ndF` eller `Shift` innan du trycker på `sin`-tangenten. Oavsett vilken metod du använder för att lösa detta exempel, bör du i alla fall hitta en vinkel på 30 grader.
Beräkna vinklar
I geometri är en vinkel utrymmet mellan två strålar eller linjesegment som har samma ändpunkt eller vertex. Det vanligaste sättet att mäta vinklar är i grader, där en hel cirkel är 360 grader. Du kan beräkna vinkeln i en polygon om du känner till polygonens form och storleken på de andra vinklarna eller, i fallet med en rätvinklig triangel, om du vet storleken på de två sidorna.
Steg
Metod 1 av 2: Beräkna vinkeln i en polygon

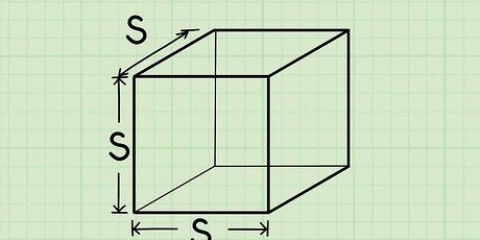
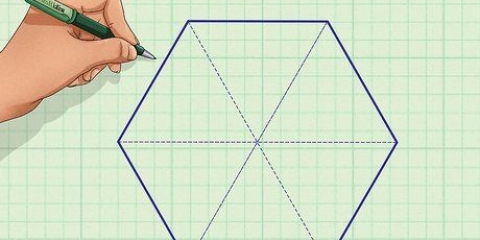
1. Räkna antalet sidor av polygonen.

2. Hitta summan av alla vinklar i polygonen. Formeln för att hitta det totala måttet av alla inre vinklar i en polygon är (n – 2) x 180, där n är antalet sidor, såväl som antalet vinklar för polygonen. Några vanliga summor av vinklarna i en polygon är:

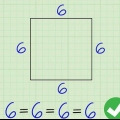
3. Bestäm om polygonen är en vanlig polygon. En vanlig polygon är en polygon med alla sidor lika långa och alla vinklar lika stora. Liksidiga trianglar och fyrkanter är exempel på vanliga polygoner, medan Pentagon i Washington DC är ett exempel på en vanlig femhörning, och ett stopptecken är ett exempel på en vanlig oktagon.

4. Addera de kända vinklarna för polygonen och subtrahera summan från summan av alla vinkelmått för polygonen. De flesta liknande geometriproblem fungerar med trianglar eller fyrhörningar eftersom det finns färre tal att bearbeta, och så kommer vi att.
Metod 2 av 2: Beräkna vinkeln i en rätvinklig triangel

1. Ta reda på vad du redan vet. En rät triangel kallas så eftersom en av dess vinklar är en rät vinkel. Du kan bestämma de andra vinklarna om du känner till något av följande:
- Storleken på den tredje vinkeln. I det här fallet kan du lägga till storleken på vinkeln till 90, antalet grader av den räta vinkeln och sedan subtrahera summan från 180.
- Storleken på två sidor av triangeln. I det här fallet kan du bestämma storleken på vinkeln med hjälp av trigonometri.

2. Bestäm vilken trigonometrisk funktion som ska användas. Trigonometriska funktioner är förhållanden mellan två av de tre sidorna i en triangel. Även om det finns sex trigonometriska funktioner, är följande tre vanligast:

3. Hitta förhållandet mellan de två kända sidorna. För detta exempel, antag att sidan mitt emot vinkeln har en längd av 5 och hypotenusan har en längd av 10. Eftersom motsatsen och hypotenusan alltså är givna, är förhållandet vi här har att göra med sinus.

4. Hitta vinkeln som motsvarar förhållandet mellan den trigonometriska funktionen. Eftersom vi använder sinus för att hitta vinkeln, kallas vinkeln vi letar efter båge eller invers sinus. Det finns två sätt att hitta det:
Tips
- Vinklar refereras till med antalet grader de mäter. Som nämnts ovan har en rät vinkel 90 grader. En vinkel större än 0 men mindre än 90 grader är en spetsig vinkel. En vinkel större än 90 men mindre än 180 grader är en trubbig vinkel. En vinkel på 180 grader är en rät vinkel, medan en vinkel större än 180 grader är en återinträdande vinkel.
- Två vinklar med totalt 90 grader kallas komplementära vinklar (de två andra vinklarna än den räta vinkeln i en rätvinklig triangel är komplementära vinklar). Två vinklar vars vinklar summerar till 180 grader kallas kompletterande vinklar.
Förnödenheter
- Trigonometriska tabeller eller en miniräknare med trigonometriska funktioner
Оцените, пожалуйста статью