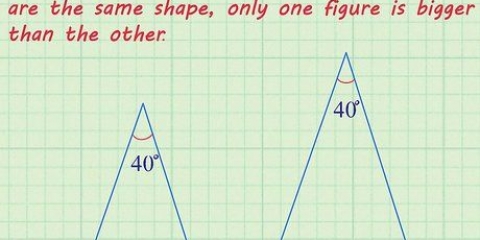
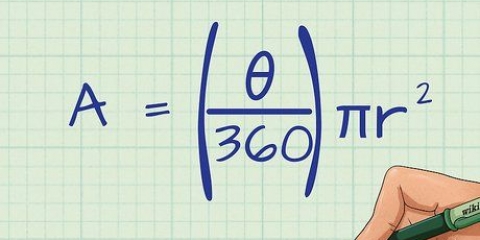Till exempel: en triangel med punkter (4, 6), (1, 2) och (1, 8). 

Till exempel: punkterna (4, 6), (1, 2) och (1, 8) blir sedan (-6, 4), (-2, 1) och (-8, 1). 


Du kan till exempel ha en diamant med poäng (4, 6), (-4, 6), (-2, -1) och (2, -1). 

Till exempel blir punkterna (4, 6), (-4, 6), (-2, -1) och (2, -1) (-4, -6), (4, -6), ( 2, 1) och (-2, 1). 


Till exempel kan du ha en triangel med punkterna (4, 6), (1, 2) och (1, 8). 

Till exempel: punkterna (4, 6), (1, 2) och (1, 8) blir sedan (6, -4), (2, -1) och (8, -1). 
Rotera en matematisk form
En rotation är en typ av geometrisk transformation där en forms hörn roteras i en viss vinkel runt en fast punkt (den så kallade rotationscentrum). I enklare termer, föreställ dig att du sticker en triangel på sekundvisaren på en klocka som vänder bakåt. Vanligtvis uppmanas du att rotera en form runt origo, vilket är punkten (0, 0) på ett koordinatplan. Du kan rotera former 90, 180 eller 270 grader runt ursprunget med hjälp av tre grundläggande formler.
Steg
Metod 1 av 3: Rotera en form 90 grader runt origo

1. Lägg märke till hur motsvarande rotationer är medurs och moturs. Att rotera en form 90 grader är detsamma som att rotera den 270 grader medurs.Konventionen är att när former roterar på ett koordinatplan, roterar de moturs (till vänster). Du kan anta detta, om inte annat anges i uttalandet.
- Till exempel, om problemet lyder "Rotera formen 90 grader runt origo" kan du anta att du måste rotera formen moturs.
- Du kan lösa det här problemet på samma sätt som "Rotera formen 270 grader medurs runt origo".
- Eller: `Rotera den här formen -270 grader runt ursprunget`.

2. Hitta koordinaterna för de ursprungliga hörnen. Om dessa inte redan är givna, bestäm koordinaterna från grafen. Kom ihåg att punkternas koordinater representeras av formeln  , varigenom
, varigenom  är lika med punkten på den horisontella axeln (x-axeln) och
är lika med punkten på den horisontella axeln (x-axeln) och är lika med punkten på vertikalen (y-axeln).
är lika med punkten på vertikalen (y-axeln).
 , varigenom
, varigenom  är lika med punkten på den horisontella axeln (x-axeln) och
är lika med punkten på den horisontella axeln (x-axeln) och är lika med punkten på vertikalen (y-axeln).
är lika med punkten på vertikalen (y-axeln).
3. Ställ in formeln för att rotera en form 90 grader. Formeln är  . Den här formeln visar att du speglar formen och sedan vänder den.
. Den här formeln visar att du speglar formen och sedan vänder den.
 . Den här formeln visar att du speglar formen och sedan vänder den.
. Den här formeln visar att du speglar formen och sedan vänder den.
4. Koppla in koordinaterna i formeln. Se till att du inte anger dina x- och y-koordinater fel. I denna formel tar du det negativa av y-värdet och ändrar sedan ordningen på koordinaterna.

5. Rita den nya formen. Sätt ut de nya hörnen på planet. Anslut dina prickar med en rak linje. Den resulterande formen visar den ursprungliga formen roterad 90 grader runt ursprunget.
Metod 2 av 3: Rotera en form 180 grader runt origo

1. Se vad motsvarande rotationer medurs och moturs är. Eftersom en hel rotation är 360 grader, är att vrida en form 180 grader medurs detsamma som att vrida 180 grader moturs.
- Om problemet säger att du ska rotera formen 180 grader runt origo, kan du anta att du vrider formen moturs.
- Du kan lösa det här problemet på samma sätt som för ett problem som "Rotera formen 180 grader medurs runt origo.".
- Du kan också stöta på något i stil med: "Rotera den här formen -180 grader runt utgångspunkten".

2. Skriv ner koordinaterna för toppen av den ursprungliga formen. Dessa kommer förmodligen att ges. Om inte, bör du kunna härleda dem från koordinatgrafen. Glöm inte att skriva koordinaterna för varje vertex i ett (x,y) format.

3. Ställ in formeln för att rotera en form 180 grader. Formeln är . Denna formel visar att du speglar formen två gånger.
. Denna formel visar att du speglar formen två gånger.
 . Denna formel visar att du speglar formen två gånger.
. Denna formel visar att du speglar formen två gånger.
4. Bearbeta koordinaterna i formeln. Se till att bearbeta rätt koordinater i rätt position för det nya beställda paret. I denna formel förblir x- och y-värdena i samma position, men du tar det negativa värdet för varje koordinat.

5. Rita den nya formen. Sätt ut de nya hörnen på planet. Anslut dina prickar med en rak linje. Den resulterande formen visar den ursprungliga formen, men roterad 180 grader runt ursprunget.
Metod 3 av 3: Rotera en form 270 grader runt origo

1. Notera vilka motsvarande rotationer det finns medurs och moturs. Att rotera en form 270 grader är samma sak som att vrida den 90 grader medurs. Former roteras moturs på ett koordinatplan enligt konvention. Du kan anta att så är fallet, om inte annat anges i uttalandet.
- Till exempel, om problemet lyder "Rotera formen 270 grader runt origo" kan du anta att du vrider formen moturs.
- Du skulle lösa det här problemet på samma sätt som för ett problem som heter så här: `Rotera formen 90 grader medurs runt origo`.
- Du kan också stöta på något i stil med: "Rotera den här formen -90 grader runt ursprunget".

2. Bestäm koordinaterna för de ursprungliga hörnen. Denna information ges, eller så bör du lätt kunna hitta koordinaterna genom att titta på grafen.

3. Ställ in formeln för att rotera en form 270 grader. Formeln är  . Detta indikerar att du kommer att spegla formen och sedan vända den.
. Detta indikerar att du kommer att spegla formen och sedan vända den.
 . Detta indikerar att du kommer att spegla formen och sedan vända den.
. Detta indikerar att du kommer att spegla formen och sedan vända den.
4. Bearbeta koordinaterna i formeln. Se till att du inkluderar rätt x- och y-värden i det nya koordinatparet. I denna formel är x- och y-värdena omvända och du tar det negativa värdet på x-koordinaten.

5. Rita den nya formen. Rita de nya punkterna i planet. Använd en linjal för att koppla ihop dem. Den resulterande formen visar den ursprungliga formen, men roterad 270 grader runt ursprunget.
"Rotera en matematisk form"
Оцените, пожалуйста статью